- Recording DME with the LimeSDR
DME (distance measuring equipment) is an aircraft radio navigation system that is used to measure the distance between an aircraft and a DME station on ground. DME is often colocated with a VOR station, in which case the VOR provides the bearing information. DME works by measuring the two-way time of flight of pulse pairs, which are first transmitted by the aircraft, then retransmitted with a fixed delay by the ground station, which acts as a transponder, and finally received back by the aircraft. DME operates between 960 and 1215 MHz. It is channelized in steps of 1 MHz, and the air-to-ground and ground-to-air frequencies always differ by 63 MHz (here is a list of all the frequency channels).
I want to write a post explaining in detail how DME works by analysing a recording of DME that contains both the air-to-ground and the ground-to-air channels. Among other things, I want to show that the delay between the aircraft and ground station pulses matches the one calculated using the aircraft position (which I can get from ADS-B data on the internet), the ground station position, the position of the recorder, and the fixed delay applied by the ground station transponder.
Recording two channels 63 MHz apart is tricky with the kind of SDRs I have. Devices based on the AD9361 technically support a maximum sample rate of 61.44 Msps (although some people are running it at up to 122.88 Msps). The LMS7002M, which is used by the LimeSDR and other SDRs, is an interesting alternative, for two reasons. First, it supports more than 61.44 Msps. However, it isn’t clear what is the maximum sample rate supported by the LimeSDR. Some sources, including the LimeSDR webpage mention 61.44 MHz bandwidth, but the LMS7002M datasheet says that the maximum RF modulation bandwidth (whatever that means) through the digital interface in SISO mode is 96 MHz. In the case of the LimeSDR there is also the limitation of the USB3 data rate, but this should not be a problem if we use only 1 RX channel. I haven’t found clear information about the limitations of each of the components of the LMS7002M (ADC max sample rate, etc.).
The second interesting feature is that the LMS7002M has a DDC on the chip. The AD9361 has a series of decimating filters to reduce the ADC sample rate and deliver a lower sample rate through the digital interface. The LMS7002M, in addition to this, has an NCO and digital mixer that can be be used to apply a frequency shift to the ADC IQ signal before decimation.
I had two different ideas about how to use the LimeSDR to record the two DME channels. The first idea consisted in using a 70 Msps output sample rate. For this I used an ADC sample rate of 140 Msps, because I think it is necessary to have at least decimation by 2 after the ADC (the LMS7200M documentation does not explain this clearly, so figuring out how to use the chip often involves some trial and error using
LimeSuiteGUI). This idea had two problems. The first problem is that some CGEN PLL occasionally failed to lock when using an ADC sample rate of 140 Msps. However the LimeSuite driver retried multiple times until the PLL locked, so in practice this wasn’t a problem. This approach worked well on my desktop PC, since in 70 Msps I had the two DME channels and then I could use GNU Radio to extract each of the two channels (for instance with the Frequency Xlating FIR Filter). However, the laptop I planned to use to record on the field couldn’t keep up with 70 Msps.The second idea was to use the on-chip DDC in the LMS7200M to extract the DME channel and deliver a much lower sample rate over the digital interface. The figure below shows how the LMS7200M digital signal processing datapath works. This datapath is called RXTSP. The RXI and RXQ signals are the digital signals coming from the ADC (here and below, by ADC I mean a dual-channel ADC, since the LMS7002M is a zero-if IQ transceiver). The RYI and RYQ are the signals delivered to the digital interface of the chip. Since the LMS7200M has two RX channels, there are two identical chains, one for each channel. The parameters of each chain can be programmed completely independently.
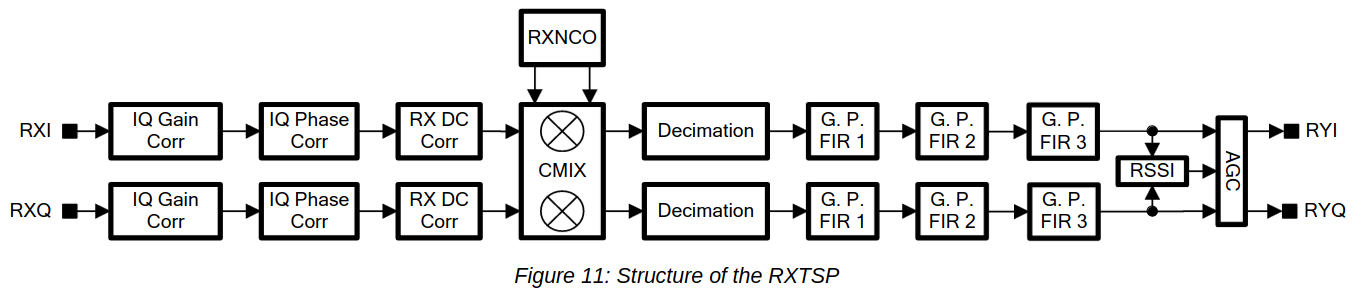
LMS7200M digital signal processing, extracted from the datasheet There is no way of sending the signal of one ADC to the two RXTSPs. The connection between each ADC and its corresponding RXTSP is fixed. Therefore, we need to feed in the antenna signal through the two RX channels, but we can easily do this with an external splitter. Remember that both of the LMS7200M RX channels share the same LO, as illustrated by the block diagram below. So the point here is to tune the LO to a frequency between the two DME channels, set the sample rate high enough that both DME channels are present in the ADC output, and finally to use each of the two RXTSPs to extract one of the DME channels, sending it at a low sample rate through the digital interface.
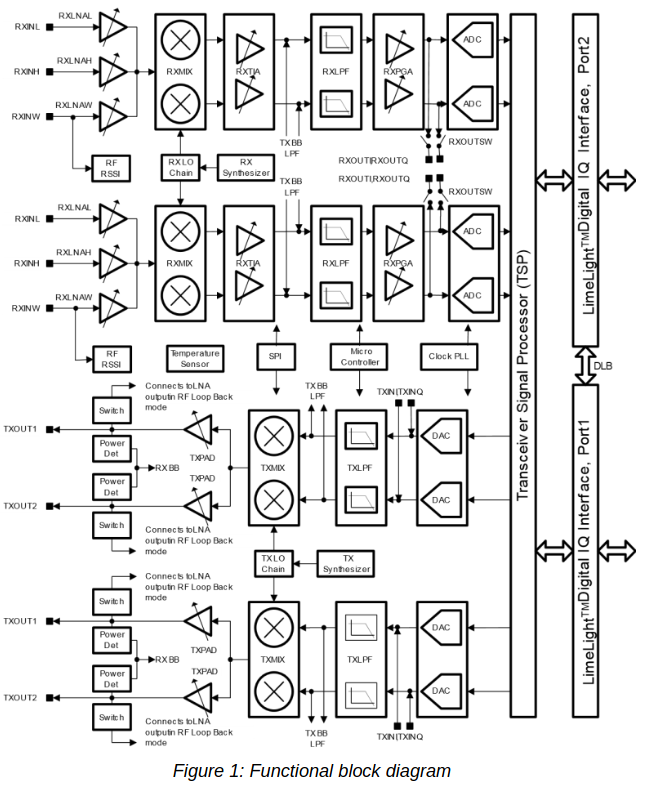
LMS7200M block diagram, extracted from the datasheet This approach has worked quite well. I have set the ADC to 80 Msps and used the RXTSPs to dowconvert and decimate the DME channels to 2.5 Msps, recording that data directly in GNU Radio.
I have done a two hour recording of DME and published it in the Zenodo dataset Recording of Colmenar (CNR) VOR-DME air-to-ground and ground-to-air DME channels.
In the rest of this post I explain the details of the recording set up and do a preliminary analysis of the recording quality.
- LTE uplink: PUSCH
This post belongs to my series about LTE. In the LTE uplink, the PUSCH (physical uplink shared channel) is the channel used to trasmit data from the UEs (phones) to the eNB (base station). It plays a role analogous to the PDSCH (physical downlink shared channel), which is used to transmit data in the downlink. In this post I will decode the PUSCH in a recording that I made of my phone uplink a couple years ago.
The PUSCH uses the same kind of techniques as the PDSCH for transport block coding, so all the Turbo code implementation and related algorithms from my post about the PDSCH will be re-used here. However, there is an important difference between the PDSCH and the PUSCH that makes decoding the PUSCH much harder. The LTE downlink is, in a certain sense, a self-descriptive signal. The UEs don’t know in advance the configuration that will be used to transmit each transport block in the PDSCH, because the eNB decides it on the fly. Therefore, the eNB announces PDSCH transmissions in the PDCCH (physical downlink control channel).
When I decoded the PDCCH and PDSCH, the only slightly clever thing that I had to do was to find the RNTIs (radio network temporary indicators). These are 16-bit numbers that are used to address each PDSCH transmission. There are some of them which are statically allocated to some broadcast purpose (SI-RNTI, P-RNTI, RA-RNTI), and the C-RNTIs, which are individually assigned to each UE. The CRC-16 of the PDCCH DCIs is XORed with the RNTI to which the transmission is addressed. At any time, a UE knows the set of RNTIs that it is monitoring, so it calculates the CRC-16 of the received DCI, computes its XOR with each of its assigned RNTIs, and compares the result with the CRC-16 in the DCI. If there is a match, the DCI is accepted. This is a way of filtering out messages without spending additional bits to put the RNTI in a field in the DCI.
When we are monitoring an LTE downlink, we don’t know which RNTIs are being used. With some cleverness, if the SNR is good enough, we can detect and select each PDCCH transmission by hand (it is necessary to guess the REGs that it occupies and the DCI length) and then, assuming that we have decoded the DCI with no bit errors, obtain the RNTI as the XOR of the calculated CRC and the received CRC. This is what I did in the post about the PDCCH. If we were monitoring the LTE downlink for a longer time, this trick wouldn’t even be necessary. The C-RNTIs assigned to the UEs are communicated to them in a RAR transmitted with the RA-RNTI, as a response to their PRACH (see the post where I analyze this in Wireshark). So a downlink monitor application can simply watch the SI-RNTI, P-RNTI and RA-RNTI, and add any C-RNTIs to a list of known connected UEs when it sees a RAR. The C-RNTIs can be removed from this list after a period of inactivity, because the UE would have been sent to the idle state by the network. This idea really shows that it is possible to decode everything in the LTE downlink without doing clever blind decoding tricks.
In contrast, the LTE uplink is not self-descriptive. The eNB defines the configuration of each PUSCH transmission when it sends the uplink grant to the UE. So the UE doesn’t need to communicate this configuration again to the eNB when it transmits in the PUSCH. The information that describes the PUSCH transmissions is effectively in the PDCCH in the downlink, and in this case I don’t have a recording of the downlink that matches my uplink recording. This makes decoding the PUSCH much more difficult, but nevertheless not impossible. With some clever ideas and blind decoding tricks we can usually find all the information we’re missing. In the rest of this post, I describe how to do this in detail. It will be long and quite technical.
- Computing PLL coefficients
Whenever I implement a PLL or a similar control loop, I invariably consult the formulas in the paper Controlled-Root Formulation for Digital Phase-Locked Loops, by Stephens and Thomas. Other sources that give formulas for the loop coefficients in terms of the loop bandwidth perform a continuous time analysis and then use a bilinear transform or a similar kind of transform to translate results between continuous time and discrete time. The appeal of the paper by Stephens and Thomas is that they work directly in discrete time, using a beautiful complex contour integral argument to calculate the loop bandwidth in terms of the loop coefficients for a loop of any order. Unfortunately, their method doesn’t give a closed-form formula for the loop coefficients in terms of the loop bandwidth. The loop coefficients can be obtained numerically, and the paper gives tables for common loop bandwidths and orders.
In most of my designs I use a second order loop with supercritical damping, which means that the two loop roots in the z-plane are equal (and hence real). As I was doing a design the other day, I wondered whether in this specific situation, which is much simpler than the general case, a closed-form solution could be obtained. It turns out that this is the case, so I’ll be using this formula from now on. In this short post I explain how this is done and give the formula.
- Decoding ERMINAZ
ERMINAZ-1U and ERMINAZ-1V are upcoming 1P PocketQubes by AMSAT-DL that will be launched in Rocket Factory Augsburg first flight from SaxaVord (Shetland, UK) later this year, together with other PocketQubes from AMSAT-EA and Libre Space Foundation. The ERMINAZ-1 satellites are based on the Libre Space QUBIK design and use the same communications system. Recently I have added a decoder for the ERMINAZ-1 satellites to gr-satellites and tested it using some pre-flight recordings that the team has shared with me.
The QUBIK communications stack uses something know as OSDLP (Open Space Data Link Protocol), which was developed by Libre Space based on CCSDS. Unfortunately, there is not much documentation about OSDLP. The best I’ve found are these slides, which only speak about the Data Link and higher layers. A look at the QUBIK transceiver GNU Radio flowgraph that AMSAT-DL is using with these satellites, together with some gr-satnogs blocks used in the flowgraph has been quite useful to figure out how the Synchronization and Coding layer of QUBIK works. In the rest of this post I will document my findings.
- Decoding the LTE-M SIB-BR
LTE-M is a family of several configurations supported by LTE for machine-to-machine and IoT communications. In this post I will talk specifically about BL/CE (bandwidth reduced low complexity / coverage enhancement), which is also known as LTE Cat M1. The main difference between a BL/CE UE and a regular LTE UE is that a BL/CE UE only supports a bandwidth of 1.4 MHz (in practice, 6 resource blocks, or 1.08 MHz) and can be half-duplex. These limitations reduce the cost, size and power of the UE, but require additional techniques to handle them.
If we think about the downlink, there are several signals that occupy the whole cell bandwidth, which is usually larger than 1.4 MHz. These are the PDCCH (physical downlink shared channel), the PCFICH (physical control format indicator channel) and the PHICH (physical hybrid-ARQ indicator channel). A BL/CE UE cannot receive any of these, so alternative signals must be used to provide similar functionality. Additionally, a BL/CE UE needs guard intervals in the time domain to support retuning of the 1.4 MHz slice in which the UE operates, and transmit/receive switching for half-duplex UEs. Another distinguishing feature of BL/CE is that messages are often repeated multiple times in order to support working with worse signal conditions than what is possible with a regular UE.
In LTE, the PSS and SSS (primary synchronization signal and secondary synchronization signal), as well as the PBCH (physical broadcast channel) occupy the central 6 resource blocks, so a BL/CE UE can synchronize to the cell and decode the MIB transmitted in the PBCH. The next step that a regular UE would perform is to monitor the PDCCH, first to find a SIB1 transmission (which is transmitted in the PDSCH), and then the rest of the SIBs (whose transmission schedule is listed in the SIB1). A BL/CE UE cannot do this, because it cannot receive the PDCCH and because the SIB PDSCH transmissions might be wider than 6 resource blocks. Therefore, in a cell that supports BL/CE UEs there are also SIB-BRs (BR stands for bandwidth reduced), which BL/CE UEs use instead of the regular SIBs. The SIB-BRs occupy 6 resource blocks and do not require receiving the PDCCH to be decoded. In this post I will use my recording of an LTE eNB to show how to decode the SIB-BRs, and other important aspects of BL/CE UEs.
10ghz artemis1 astronomy astrophotography ATA ccsds ce5 contests digital modes doppler dslwp dsp eshail2 fec freedv frequency gmat gnss gnuradio gomx hermeslite hf jt kits lilacsat limesdr linrad lte microwaves mods moonbounce noise ofdm orbital dynamics outernet polarization radar radioastronomy radiosonde rust satellites sdr signal generators tianwen vhf & uhf