You might remember that back in July I made a recording of the DME ground-to-air and air-to-ground frequencies for a nearby VOR-DME station. In that post, I performed a preliminary analysis of the recording. I mentioned that I was interested in measuring the delay between the signals received directly from the aircraft and the ground transponder replies, and match these to the aircraft trajectories. This post is focused on that kind of study. I will present a GNU Radio out-of-tree module gr-dme that I have written to detect and measure DME pulses, and show a Jupyter notebook where I match aircraft pulses with their corresponding ground transponder replies and compare the delays to those calculated from the aircraft positions given in ADS-B data.
Category: Experiments
Measurements, transmissions, receptions, etc. with the objective of obtaining and analysing some data.
Recording DME with the LimeSDR
DME (distance measuring equipment) is an aircraft radio navigation system that is used to measure the distance between an aircraft and a DME station on ground. DME is often colocated with a VOR station, in which case the VOR provides the bearing information. DME works by measuring the two-way time of flight of pulse pairs, which are first transmitted by the aircraft, then retransmitted with a fixed delay by the ground station, which acts as a transponder, and finally received back by the aircraft. DME operates between 960 and 1215 MHz. It is channelized in steps of 1 MHz, and the air-to-ground and ground-to-air frequencies always differ by 63 MHz (here is a list of all the frequency channels).
I want to write a post explaining in detail how DME works by analysing a recording of DME that contains both the air-to-ground and the ground-to-air channels. Among other things, I want to show that the delay between the aircraft and ground station pulses matches the one calculated using the aircraft position (which I can get from ADS-B data on the internet), the ground station position, the position of the recorder, and the fixed delay applied by the ground station transponder.
Recording two channels 63 MHz apart is tricky with the kind of SDRs I have. Devices based on the AD9361 technically support a maximum sample rate of 61.44 Msps (although some people are running it at up to 122.88 Msps). The LMS7002M, which is used by the LimeSDR and other SDRs, is an interesting alternative, for two reasons. First, it supports more than 61.44 Msps. However, it isn’t clear what is the maximum sample rate supported by the LimeSDR. Some sources, including the LimeSDR webpage mention 61.44 MHz bandwidth, but the LMS7002M datasheet says that the maximum RF modulation bandwidth (whatever that means) through the digital interface in SISO mode is 96 MHz. In the case of the LimeSDR there is also the limitation of the USB3 data rate, but this should not be a problem if we use only 1 RX channel. I haven’t found clear information about the limitations of each of the components of the LMS7002M (ADC max sample rate, etc.).
The second interesting feature is that the LMS7002M has a DDC on the chip. The AD9361 has a series of decimating filters to reduce the ADC sample rate and deliver a lower sample rate through the digital interface. The LMS7002M, in addition to this, has an NCO and digital mixer that can be be used to apply a frequency shift to the ADC IQ signal before decimation.
I had two different ideas about how to use the LimeSDR to record the two DME channels. The first idea consisted in using a 70 Msps output sample rate. For this I used an ADC sample rate of 140 Msps, because I think it is necessary to have at least decimation by 2 after the ADC (the LMS7200M documentation does not explain this clearly, so figuring out how to use the chip often involves some trial and error using LimeSuiteGUI). This idea had two problems. The first problem is that some CGEN PLL occasionally failed to lock when using an ADC sample rate of 140 Msps. However the LimeSuite driver retried multiple times until the PLL locked, so in practice this wasn’t a problem. This approach worked well on my desktop PC, since in 70 Msps I had the two DME channels and then I could use GNU Radio to extract each of the two channels (for instance with the Frequency Xlating FIR Filter). However, the laptop I planned to use to record on the field couldn’t keep up with 70 Msps.
The second idea was to use the on-chip DDC in the LMS7200M to extract the DME channel and deliver a much lower sample rate over the digital interface. The figure below shows how the LMS7200M digital signal processing datapath works. This datapath is called RXTSP. The RXI and RXQ signals are the digital signals coming from the ADC (here and below, by ADC I mean a dual-channel ADC, since the LMS7002M is a zero-if IQ transceiver). The RYI and RYQ are the signals delivered to the digital interface of the chip. Since the LMS7200M has two RX channels, there are two identical chains, one for each channel. The parameters of each chain can be programmed completely independently.
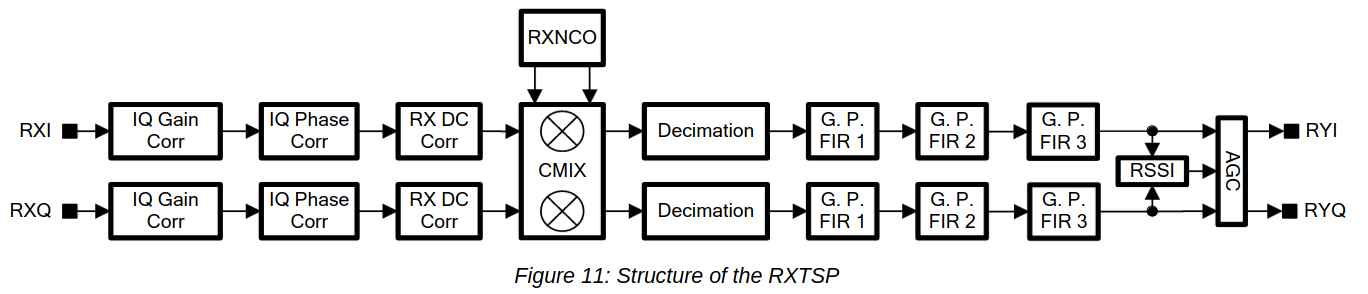
There is no way of sending the signal of one ADC to the two RXTSPs. The connection between each ADC and its corresponding RXTSP is fixed. Therefore, we need to feed in the antenna signal through the two RX channels, but we can easily do this with an external splitter. Remember that both of the LMS7200M RX channels share the same LO, as illustrated by the block diagram below. So the point here is to tune the LO to a frequency between the two DME channels, set the sample rate high enough that both DME channels are present in the ADC output, and finally to use each of the two RXTSPs to extract one of the DME channels, sending it at a low sample rate through the digital interface.
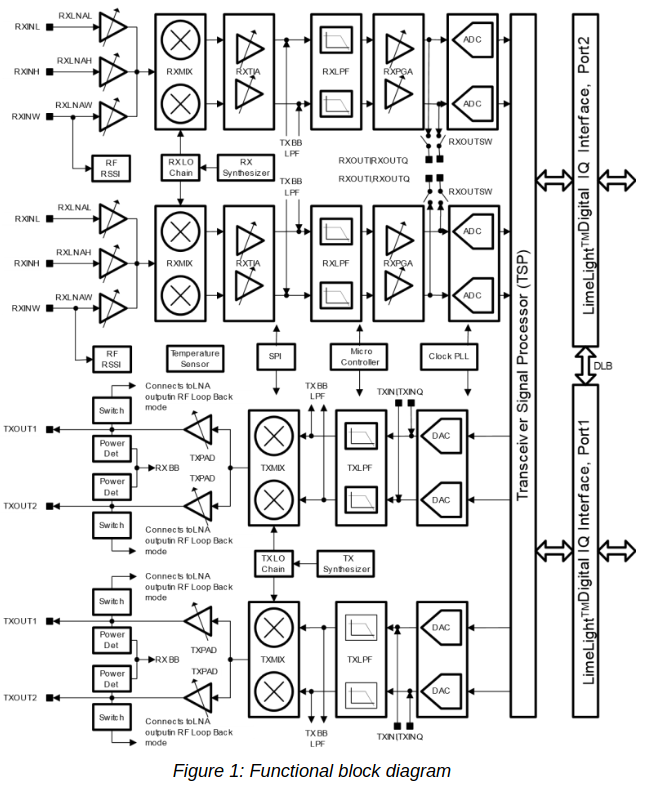
This approach has worked quite well. I have set the ADC to 80 Msps and used the RXTSPs to dowconvert and decimate the DME channels to 2.5 Msps, recording that data directly in GNU Radio.
I have done a two hour recording of DME and published it in the Zenodo dataset Recording of Colmenar (CNR) VOR-DME air-to-ground and ground-to-air DME channels.
In the rest of this post I explain the details of the recording set up and do a preliminary analysis of the recording quality.
Receiving HADES-D
HADES-D is the 9th PocketQube developed by AMSAT-EA. It is the first one that hasn’t failed early in the mission. Among the previous AMSAT-EA satellites, GENESIS-L and -N suffered the launch failure of the Firefly-Alpha maiden flight, EASAT-2 and HADES presumably failed to deploy their antennas, GENESIS-G and -J flew on the second Firefly-Alpha flight, which only achieved a short-lived orbit, with all the satellites reentering in about a week, URESAT-1 had the same kind of antenna deployment problem, and GENESIS-A is a short duration payload scheduled to fly in the Ariane-6 maiden flight, which hasn’t happened yet.
HADES-D launched with the SpaceX Transporter 9 rideshare on November 11. This PocketQube was carried in the ION SCV-013 vehicle, and was released on November 28. The antennas have been deployed correctly, unlike in its predecessors, the satellite is in good health, and several amateur stations have been able to receive it successfully, so congratulations to AMSAT-EA.
Since HADES-D is the first PocketQube from AMSAT-EA that is working well, I was curious to measure the signal strength of this satellite. Back around 2016 I was quite involved in the early steps of AMSAT-EA towards their current line of satellites. We did some trade-offs between PocketQube and cubesat sizes and calculated power budgets and link budgets. Félix Páez EA4GQS and I wanted to build an FM repeater amateur satellite, because that suited best the kind of portable satellite operations with a handheld yagi that we used to do back then. Using a PocketQube for this always seemed a bit of a stretch, since the power available wasn’t ample. In fact, around the time that PocketQubes were starting to appear, some people were asking if this platform could ever be useful for any practical application.
Fast forward to the end of 2023 and we have HADES-D in orbit, with a functioning FM repeater. My main interest in this satellite is to gather more information about these questions. I should say that I was only really active in AMSAT-EA’s projects during 2016. Since then, I have lost most of my involvement, only receiving some occasional informal updates about their work.
A very quick RFI survey at the Allen Telescope Array
At the beginning of August I visited the Allen Telescope Array (ATA) for the Breakthrough Listen REU program field trip (I have been collaborating with the REU program for the past few years). One of the things I did during my visit was to use an ADALM Pluto running Maia SDR to do a very quick scan of the radio frequency interference (RFI) on-site. This was not intended as a proper study of any sort (for that we already have the Hat Creek Radio Observatory National Dynamic Radio Zone project), but rather as a spoor-of-the-moment proof of concept.
The idea was to use equipment I had in my backpack (the Pluto, a small antenna, my phone and a USB cable), step just outside the main office, scroll quickly through the spectrum from 70 MHz to 6 GHz, stop when I saw any signals (hopefully not too many, since Hat Creek Radio Observatory is supposed to be a relatively quiet radio location), and make a SigMF recording of each of the signals I found. It took me about 15 minutes to do this, and I made 6 recordings in the process. A considerable amount of time was spent downloading the recordings to my phone, which takes about one minute per recording (since recordings are stored on the Pluto DDR, only one recording can be stored on the Pluto at a time, and it must be downloaded to the phone before making a new recording).
This shows that Maia SDR can be a very effective tool to get a quick idea of how the local RF environment looks like, and also to hunt for local RFI in the field, since it is quite easy to carry around a Pluto and a phone. The antenna I used was far from ideal: a short monopole for ~450 MHz, shown in the picture below. This does a fine job at receiving strong signals regardless of frequency, but its sensitivity is probably very poor outside of its intended frequency range.
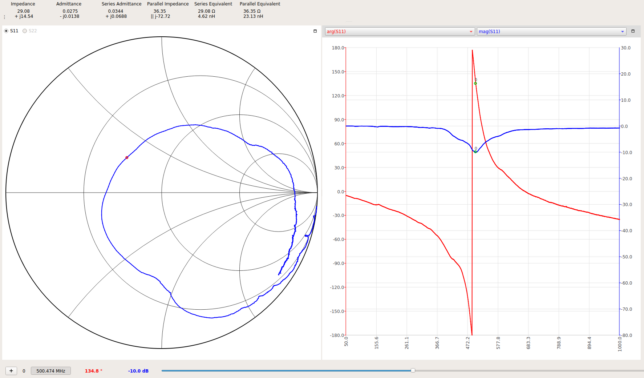
The following plot shows the impedance of the antenna measured with a NanoVNA V2. The impedance changes noticeably if I put my hand on the NanoVNA, with the resonant peak shifting down in frequency by 50 to 100 MHz. Therefore, this measurement should be taken just as a rough ballpark of how the antenna looks like on the Pluto, which I was holding with my hand.
As the antenna I used for this survey is pretty bad, the scan will only show signals that are actually very strong on the ATA dishes. The log-periodic feeds on the ATA dishes tend to pick up signals that do not bounce off the dish reflectors, and instead arrive to the feed directly from a side. This is different from a waveguide type feed, in which signals need to enter through the waveguide opening. Therefore, besides having the main lobe corresponding to a 6.1 m reflector, the dishes also have relatively strong sidelobes in many directions, with a gain roughly comparable to an omnidirectional antenna. The system noise temperature of the dishes is around 100 to 150 K (including atmospheric noise and spillover), while the noise figure of the Pluto is probably around 5 dB. This all means that the dishes are more sensitive to detect signals from any direction that the set up I was using. In fact, signals from GNSS satellites from all directions can easily be seen with the dishes several dB above the noise floor, but not with this antenna and the Pluto.
Additionally, the scan only shows signals that are present all or most of the time, or that I just happened to come across by chance. This quick survey hasn’t turned up any new RFI signals. All the signals I found are signals we already knew about and have previously encountered with the dishes. Still, it gives a good indication of what are the strongest sources of RFI on-site. Something else to keep in mind is that the frequency range of the Allen Telescope Array is usually taken as 1 – 12 GHz. Although the feeds probably work with some reduced performance somewhat below 1 GHz, observations are done above 1 GHz. Therefore, none of the signals I have detected below 1 GHz are particularly important for the telescope observations, since they are not strong enough to cause out-of-band interference.
I have published the SigMF recordings in the Zenodo dataset Quick RFI Survey at the Allen Telescope Array. All the recordings have a sample rate of 61.44 Msps, since this is what I was using to view the largest possible amount of spectrum at the same time, and a duration of 2.274 seconds, which is what fits in 400 MiB of the Pluto DDR when recording at 61.44 Msps 12 bit IQ (this is the maximum recording size for Maia SDR). The published files are as produced by Maia SDR. At some point it could be interesting to add additional metadata and annotations.
In the following, I do a quick description of each of the 6 recordings I made.
More about the QO-100 WB transponder power budget
Last week I wrote a post with a study about the QO-100 WB transponder power budget. After writing this post, I have been talking with Dave Crump G8GKQ. He says that the main conclusions of my study don’t match well his practical experience using the transponder. In particular, he mentions that he has often seen that a relatively large number of stations, such as 8, can use the transponder at the same time. In this situation, they “rob” much more power from the beacon compared to what I stated in my post.
I have looked more carefully at my data, specially at situations in which the transponder is very busy, to understand better what happens. In this post I publish some corrections to my previous study. As we will see below, the main correction is that the operating point of 73 dB·Hz output power that I had chosen to compute the power budget is not very relevant. When the transponder is quite busy, the output power can go up to 73.8 dB·Hz. While a difference of 0.8 dB might not seem much, there is a huge difference in practice, because this drives the transponder more towards saturation, decreasing its gain and robbing more output power from the beacon to be used by other stations.
I want to thank Dave for an interesting discussion about all these topics.
Measuring the QO-100 WB transponder power budget
The QO-100 WB transponder is an S-band to X-band amateur radio transponder on the Es’hail 2 GEO satellite. It has about 9 MHz of bandwidth and is routinely used for transmitting DVB-S2 signals, though other uses are possible. In the lowermost part of the transponder, there is a 1.5 Msym QPSK 4/5 DVB-S2 beacon that is transmitted continuously from a groundstation in Qatar. The remaining bandwidth is free to be used by all amateurs in a “use whatever bandwidth is free and don’t interfere others” basis (there is a channelized bandplan to put some order).
From the communications theory perspective, one of the fundamental aspects of a transponder like this is how much output power is available. This sets the downlink SNR and determines whether the transponder is in the power-constrained regime or in the bandwidth-constrained regime. It indicates the optimal spectral efficiency (bits per second per Hz), which helps choose appropriate modulation and FEC parameters.
However, some of the values required to do these calculations are not publicly available. I hear that the typical values which would appear in a link budget (maximum TWTA output power, output power back-off, antenna gain, etc.) are under NDA from MELCO, who built the satellite and transponders.
I have been monitoring the WB transponder and recording waterfall data of the downlink with my groundstation for three weeks already. With this data we can obtain a good understanding of the transponder behaviour. For example, we can measure the input power to output power transfer function, taking advantage of the fact that different stations with different powers appear and disappear, which effectively sweeps the transponder input power (though in a rather chaotic and uncontrollable manner). In this post I share the methods I have used to study this data and my findings.
Monitoring the QO-100 WB transponder usage with Maia SDR
I am interested in monitoring the usage of the QO-100 WB transponder over several weeks or months, to obtain statistics about how full the transponder is, what bandwidths are used, which channels are occupied more often, etc., as well as statistics about the power of the signals and the DVB-S2 beacon. For this, we need to compute and record to disk waterfall data for later analysis. Maia SDR is ideal for this task, because it is easy to write a Python script that configures the spectrometer to a low rate, connects to the WebSocket to fetch spectrometer data, performs some integrations to lower the rate even more, and records data to disk.
For this project I’ve settled on using a sample rate of 20 Msps, which covers the whole transponder plus a few MHz of receiver noise floor on each side (this will be used to calibrate the receiver gain) and gives a frequency resolution of 4.9 kHz with Maia SDR’s 4096-point FFT. At this sample rate, I can set the Maia SDR spectrometer to 5 Hz and then perform 50 integrations in the Python script to obtain one spectrum average every 10 seconds.
Part of the interest of setting up this project is that the Python script can serve as an example of how to interface Maia SDR with other applications and scripts. In this post I will show how the system works and an initial evaluation of the data that I have recorder over a week. More detailed analysis of the data will come in future posts.
Using GSE and DVB-S2 for IP traffic
GSE (Generic Stream Encapsulation) is a protocol used to embed packets of almost any sort into the DVB data link layer. It can be used to send IP (IPv4 and IPv6) packets, Ethernet packets, etc. In my post about Blockstream Satellite, I talked about MPE, which is another way of sending IP traffic inside DVB. However, MPE is based on MPEG TS packets, so it is a far from ideal solution, given the overhead of the TS headers and the relatively small size of TS packets. GSE is a much more lightweight solution, and it’s arguably the best way of sending IP packets inside DVB.
The downside of GSE compared to MPE is that it is not supported by so many devices. Since MPE uses TS packets, it should be supported by mostly any device. The formatting of the TS packets, and thus all of the MPE stack, is handled at the application level. However, GSE is different from a stream of TS packets already the level of BBFRAMEs, so devices that handle this layer need to support GSE.
In this post I show how to set up a DVB-S2 GSE one-way link using the GNU Radio out-of-tree module gr-dvbgse and an SDR for transmission, and a MiniTiouner, Longmynd and some software I’ve written for reception.
The MiniTiouner is a DVB-S2 hardware receiver that is based on a Serit FTS4334 NIM (which uses the STV0910 DVB-S2 demodulator IC) together with a FT2232H that provides a USB2 interface for data and control. It is a very popular device within the Amateur TV community, given its affordable price and large range of supported carrier frequencies, symbol rates, and MODCODs.
The ideas in this post are also applicable to an SDR demodulation approach, which could use gr-dvbs2rx and gr-dvbgse. Using a hardware receiver solution can give some benefits over an SDR receiver, since demodulation and LDPC decoding is computationally expensive, specially at higher symbol rates and in low SNR conditions.
My final goal for this is to do some tests of two-way IP links over the QO-100 WB transponder. I think this would be a rather interesting use of the transponder, since it would open the door to many new ideas. Currently the transponder is used almost exclusively to transmit video, which by all means is good, but not very innovative after the almost 4 years now that the transponder has been in operation.
I have to give huge thanks to Brian Jordan G4EWJ and Evariste Courjard F5OEO for their interest in this project and for running many initial tests that showed that it is possible to use the MiniTiouner to receive GSE (despite the lack of clear and detailed documentation about the STV0910 register settings).
More QO-100 orbit determination
In a previous post, I showed my orbit determination experiments of the GEO satellite Es’hail 2 using the beacons transmitted from Bochum (Germany) through the QO-100 amateur radio transponder on-board this satellite. By measuring the phase difference of the BPSK and 8APSK beacons, which are spaced apart by 245 kHz in the transponder, we can compute the three-way range-rate between the transmitter at Bochum and my receiver in Spain. This data can then be used for orbit determination with GMAT.
I have continued collection more data for these experiments, so this post is an update on the results.
QO-100 orbit determination
In a previous post, I showed my experiment about measuring the phase difference of the 8APSK and BPSK beacons of the QO-100 NB transponder. The main goal of this experiment was to use this data to do orbit determination with GMAT. Over the last week I have continued these experiments and already have started to perform some orbit determination in GMAT.
Here I give an update about several aspects of the experiment, and show how I am setting up the orbit determination.
