orbital dynamics – Daniel Estévez

Tianwen-1 third anniversary

Today is the third anniversary of Tianwen-1, which was launched in 23 July 2020. During the first year of the mission I was tracking it with great detail and writing a lot of posts. A fundamental part of this work was the help of AMSAT-DL. Using its 20 metre antenna in Bochum, they tracked the spacecraft, decoded telemetry and provided live coverage of many of the key mission events in their Youtube livestream. At some point the reception of Tianwen-1’s telemetry at Bochum got completely automated, as we described in a paper in the GNU Radio Conference 2021 proceedings.

To this date, the reception continues in Bochum almost every day, when the dish is not busy with other tasks such as tracking STEREO-A. This means that we get good coverage of the spacecraft orbital data, via the state vectors transmitted in its telemetry.

To celebrate the anniversary, I have updated my plot of the orbital parameters, which I made back in March 2022. The plot covers all the remote sensing orbit, from when it started on 8 November 2021, until the present day. To my knowledge, no manoeuvres have happened in this time (perhaps small station-keeping burns would be unnoticed without more careful analysis), so the changes in the orbit are just due to perturbations by forces such as the Sun’s gravity and the oblateness of Mars.

The updated plot can be seen below. We see that the periapsis latitude changes at a steady rate of 0.598 deg/day. The remote sensing orbit was designed so that the periapsis precessed in this way, which allows the spacecraft to cover all the surface of Mars from a low altitude in 301 days. The surface has now been covered twice, since the periapsis has moved from near the north pole to the south pole and back again to the north pole.

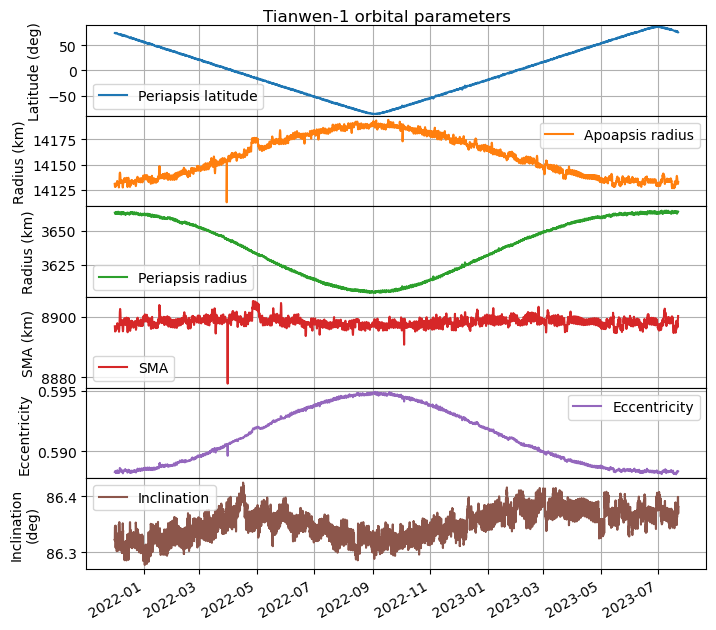
There is also an interesting change in eccentricity, which seems to be correlated with the latitude of the periapsis. The eccentricity is largest when the periapsis is over the south pole. In this case, the altitude of the periapsis decreases by 60 km, compared to when the periapsis is over the north pole. The inclination has remained mostly steady, although there seems to be a small perturbation with an amplitude of 0.1 deg.

The updated Jupyter notebook in which this plot was made can be found here.

Mars Express 20th anniversary livestream

On June 2, ESA celebrated the 20th anniversary of the launch of Mars Express (MEX) by livestreaming images of Mars from the VMC camera in a Youtube livestream. They set things up so that an image was taken by the camera approximately every 50 seconds, downlinked in the X-band telemetry to the Cebreros groundstation, which was tracking the spacecraft, and then sent to the Youtube. The total latency, according to the image timestamps that were shown in Youtube was around 17 minutes, which is quite good, since most of that latency was the 16 minutes and 45 seconds of one-way light time from Mars to Earth.

The livestream was accompanied by commentary from Simon Wood and Jorge Hernández Bernal. One of the things that got my attention during the livestream was the mention that to make the livestream work, the VMC camera should be pointing to Mars and the high-gain antenna should be pointing to Earth. This could only be done during part of Mars Express orbit, and in fact reduced the amount of sunlight hitting the solar panels, so it could not be done for too long.

This gave me the idea to use the Mars Express SPICE kernels to understand better how the geometry looked like. This is also a good excuse to show how to use SPICE.

More QO-100 orbit determination

In a previous post, I showed my orbit determination experiments of the GEO satellite Es’hail 2 using the beacons transmitted from Bochum (Germany) through the QO-100 amateur radio transponder on-board this satellite. By measuring the phase difference of the BPSK and 8APSK beacons, which are spaced apart by 245 kHz in the transponder, we can compute the three-way range-rate between the transmitter at Bochum and my receiver in Spain. This data can then be used for orbit determination with GMAT.

I have continued collection more data for these experiments, so this post is an update on the results.

QO-100 orbit determination

In a previous post, I showed my experiment about measuring the phase difference of the 8APSK and BPSK beacons of the QO-100 NB transponder. The main goal of this experiment was to use this data to do orbit determination with GMAT. Over the last week I have continued these experiments and already have started to perform some orbit determination in GMAT.

Here I give an update about several aspects of the experiment, and show how I am setting up the orbit determination.

An update about Tianwen-1’s remote sensing orbit

Tianwen-1, the Chinese Mars orbiter, entered its remote sensing orbit on November 8 2021. In a previous post, I gave an overview of the orbit using one month of state vector data collected from the spacecraft’s telemetry by AMSAT-DL using the 20 m antenna at Bochum observatory. AMSAT-DL has continued receiving telemetry almost every day, so in this post we can now look at nearly 4 months of data for the remote sensing orbit.

This orbit is a polar elliptical orbit with 86 deg inclination, a periapsis altitude of 275 km and an apoapsis radius of 14140 km. The orbital period is approximately 2/7 Mars sidereal days plus 170 seconds. This makes the ground track drift slowly towards the west, allowing the spacecraft to scan all the planet’s surface. Additionally, due to orbit perturbations, the argument of periapsis (and hence its latitude) keeps slowly changing with time. This makes possible to scan all of Mars from a low altitude.

One month of Tianwen-1 remote sensing orbit

In a previous post, I described the remote sensing orbit into which Tianwen-1 had moved on November 8. Now it has been in this orbit for more than one month, and AMSAT-DL has been collecting telemetry almost daily with the 20 metre antenna at Bochum obseratory. Therefore, it is a good moment to review the state vector data and look at how the orbit has evolved with time.

Tianwen-1 remote sensing orbit

On November 8, the Tianwen-1 orbiter made a manoeuvre to move itself to the remote sensing orbit, as reported by Chinese media. This orbit is the final orbit in the mission, as depicted in this figure from Wikipedia. The main goal of this orbit is to study the geophysical properties of Mars with all the orbiter instruments (see this paper) and to continue acting as a communications relay for the rover Zhurong.

As usual, AMSAT-DL has been collecting telemetry from Tianwen-1 with the 20 metre antenna at Bochum observatory, including spacecraft state vectors. This allows us to study the orbit change manoeuvre and the properties of the remote sensing orbit. This post is a first look at the state vector data.

Tianwen-1 landing

Yesterday, May 14th, at around 23:18 UTC the Tianwen-1 rover Zhurong safely landed on the Utopia Planitia region of Mars. To follow this event, AMSAT-DL made a 7 hour livestream of the orbiter signals as received by the 20m antenna in Bochum observatory. In this livestream we could see the signal losses caused by the manoeuvres of the deorbit burn and collision avoidance burn. Analysis of the telemetry decoded at Bochum shows more details about these manoeuvres. This post is a detailed report of the landing.

Tianwen-1 reconnaissance orbit

In my last post about Tianwen-1, I explained how on 2021-02-23 the spacecraft would enter an orbit with a period of 2 Mars sidereal days. This would give a repeating ground track with periapsis passages over the intended landing site in Utopia Planitia. Almost one month has passed since then and AMSAT-DL has continued to receive telemetry state vectors every day with the Bochum 20 meter antenna. This data allows us to study the orbit in detail, including orbit perturbations and any station-keeping manoeuvres that are done to maintain the orbit. This post is my first analysis of the current orbit.

Tianwen-1 phasing orbit

Last Saturday 2021-02-20 at 11:46:42 UTC Tianwen-1 passed the periapsis of its elliptical polar orbit at Mars and made a retrograde burn to reduce its apoapsis radius. The trajectory planning of the spacecraft can be seen in its Wikipedia page: the spacecraft first arrived into a low inclination elliptical orbit by making a Mars orbit insertion at periapsis, then coasted to apoapsis, where it performed a plane change, and then it arrived at periapsis, performing the manoeuvre described in this post.

Over the next few days the spacecraft should move into a reconnaissance orbit, which is given in Wikipedia to be a 265 x 60000 km orbit (having a period of 2 days) with an inclination of 86.9 degrees. However, the last burn hasn’t lowered the apoapsis that much. The current orbit is approximately 280 x 84600 km (3.45 day period) with an inclination of 87.7 degrees. A possible reason for using the current orbit, which has been described as a phasing orbit, will be explained in this post after reviewing the data we have about the burn.