Last Saturday 2021-02-20 at 11:46:42 UTC Tianwen-1 passed the periapsis of its elliptical polar orbit at Mars and made a retrograde burn to reduce its apoapsis radius. The trajectory planning of the spacecraft can be seen in its Wikipedia page: the spacecraft first arrived into a low inclination elliptical orbit by making a Mars orbit insertion at periapsis, then coasted to apoapsis, where it performed a plane change, and then it arrived at periapsis, performing the manoeuvre described in this post.
Over the next few days the spacecraft should move into a reconnaissance orbit, which is given in Wikipedia to be a 265 x 60000 km orbit (having a period of 2 days) with an inclination of 86.9 degrees. However, the last burn hasn’t lowered the apoapsis that much. The current orbit is approximately 280 x 84600 km (3.45 day period) with an inclination of 87.7 degrees. A possible reason for using the current orbit, which has been described as a phasing orbit, will be explained in this post after reviewing the data we have about the burn.
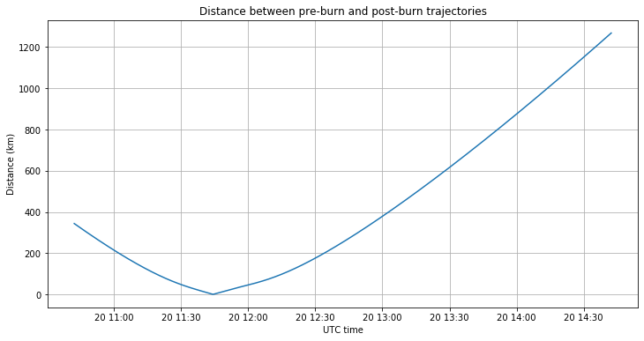
As I usually do, to compute the moment and delta-V of the burn I propagate the pre-burn and post-burn trajectories in GMAT using this script, and study the output in this Jupyter notebook. I obtain an intersection at 11:44:18 UTC, which is pretty close to the periapsis passage, so the data seems correct.
The delta-V vector in m/s using the Mars body inertial frame described in this post is
[-1.477, -1.912, 52.565]
This vector has a magnitude of 52.62 m/s. Assuming a dry mass of 2500 kg and fuel mass of 950 kg, this burn would have taken 60 seconds with the 3 kN thrusters, and spent 57 kg of fuel. Thus, according to our (somewhat crude) fuel estimates, approximately 900 kg of fuel remain now.
It is convenient to write the delta-V vector in the VNB frame whose axes are given by V, the velocity vector, N, the vector normal to the orbit (which is defined to point along the cross product of the radius and V), and B, the bi-normal vector, which is the cross product of V and N. The VNB coordinates in m/s are
[-50.406, 0.032, 15.104]
We see that most of the burn happens along -V as expected for a retrograde burn, but there is a significant component along +B. This is perhaps a bit unexpected. The effect of a +B burn is to move the periapsis backwards along the orbit, so that it would move to a slightly more northern latitude (the spacecraft descends from north to south on the periapsis passage). In fact, the periapsis has moved from a latitude of 10.03º N to a latitude of 10.25º N. This might be relevant for the discussion that comes below.
Now the good question is what is the reason for moving to this intermediate phasing orbit with a 3.45 day period instead of moving directly to the 2 day period orbit? I think there is a quite reasonable explanation, but we must first understand the purpose of the 2 day period reconnaissance orbit. This will be the orbit used by the spacecraft to map and survey the intended landing site, until the lander is released, which is expected to happen in May or June.
Therefore, it seems quite desirable to have an orbit whose periapsis ground track always passes over the landing site. This gives plenty of opportunities for gathering survey data and is also mandatory for the release of the lander, which is basically going to be done from the reconnaissance orbit (by first lowering its periapsis in a suitable manner). So all this makes me think that the quoted “2 day period” is actually 2 Mars sidereal days (a Mars sidereal day is 24 hours, 37 minutes and 22 seconds), since that would give a repeating ground track.
For this plan to work well, the periapsis of the the orbit needs to be at the correct longitude by the time that the 2 sidereal day orbit is entered. Otherwise the ground track will be repeating, but it will not pass over the landing site. Now, the longitude of the next periapsis of the current orbit turns out to be 111.3º E. In Wikipedia the coordinates of the intended landing site in Utopia Planitia are given as 24.748º N, 110.318º E. Note that the latitude of the site is somewhat higher than the latitude of the periapsis of the current orbit, so perhaps moving the periapsis north is desirable. This might (but only might) be the reason for the burn component along B.
So we see that around the next periapsis, which is going to be tomorrow 2021-02-23 at 22:31:37 UTC, the spacecraft will pass above the landing site. Given this circumstance, it can now enter the 2 sidereal day reconnaissance orbit, which will then have a repeating ground track that always passes over the landing site.
There is no magic involved in these adjustments. Coming in from the previous orbit last Saturday, when arriving to the periapsis it is just enough to adjust the apoapsis altitude (and hence the orbit period) in such a way that when the spacecraft comes to the next periapsis Mars has rotated below the orbit so as to place the longitude of the landing site below the orbit. The required period to do this will depend on the (signed) difference between the longitude of the periapsis where the burn is performed and the longitude of the landing site. Therefore, the name “phasing orbit” is completely justified. The purpose of the current orbit would be to wait until the rotation of Mars places the landing site below the orbit.
To see what the passage to the 2 sidereal day orbit at next periapsis would look like, I have made this GMAT script. By adjusting the delta-V of the periapsis burn, I have seen that a 40.9 m/s burn will give an orbit with a ground track that is very close to be repeating. This is shown in the figure below.

There is some degree of complication here regarding orbit perturbations. The plot above shows 14 days of ground track, and we see that at some point the ground track starts to slowly creep to the east. The propagator I’m using here is quite detailed: the 80×80 GMM-2B Mars gravity model, point mass forces for all planets and the Sun, relativistic effects, and an integration step of at most 50 seconds (no solar radiation pressure or atmospheric drag, though).
Something I haven’t understood completely is why the period of the orbit shown above is actually 162 seconds longer than two sidereal days. Forgetting about perturbations, the track of such an orbit would drift some 0.66 degrees to the west per revolution. However, if I try to adjust the orbit to have a period closer to 2 sidereal days, I get much more drift of the ground track than with this orbit solution. I don’t know if this is caused by perturbations or by numerical accuracy (perhaps related to the integrator). This is something that might deserve more in-depth study. In any case, probably the real-world orbit will need some degree of station keeping to correct for perturbations.
The apoapsis radius of this 2 sidereal day orbit is 61217 km (giving an apoapsis altitude of 57821 km), while the periapsis has an altitude of 282 km (logically, still close to the 280 km we started with on Saturday). Therefore, some care should be taken when quoting this as a 265 x 60000 km orbit. That can be slightly misleading, as it is not clear if 60000 km refers to the apoapsis radius or altitude.
To summarize, in this post we have shown that it is very likely that the purpose of the current orbit is to pass over the landing site at next periapsis on 2021-02-23 22:31:37 UTC. Then a burn would lower the apoapsis further to obtain an orbit with a period of 2 sidereal days that has a repeating ground track passing over the landing site.
3 comments