Yesterday, May 14th, at around 23:18 UTC the Tianwen-1 rover Zhurong safely landed on the Utopia Planitia region of Mars. To follow this event, AMSAT-DL made a 7 hour livestream of the orbiter signals as received by the 20m antenna in Bochum observatory. In this livestream we could see the signal losses caused by the manoeuvres of the deorbit burn and collision avoidance burn. Analysis of the telemetry decoded at Bochum shows more details about these manoeuvres. This post is a detailed report of the landing.
Tag: gmat
Tianwen-1 reconnaissance orbit
In my last post about Tianwen-1, I explained how on 2021-02-23 the spacecraft would enter an orbit with a period of 2 Mars sidereal days. This would give a repeating ground track with periapsis passages over the intended landing site in Utopia Planitia. Almost one month has passed since then and AMSAT-DL has continued to receive telemetry state vectors every day with the Bochum 20 meter antenna. This data allows us to study the orbit in detail, including orbit perturbations and any station-keeping manoeuvres that are done to maintain the orbit. This post is my first analysis of the current orbit.
Tianwen-1 phasing orbit
Last Saturday 2021-02-20 at 11:46:42 UTC Tianwen-1 passed the periapsis of its elliptical polar orbit at Mars and made a retrograde burn to reduce its apoapsis radius. The trajectory planning of the spacecraft can be seen in its Wikipedia page: the spacecraft first arrived into a low inclination elliptical orbit by making a Mars orbit insertion at periapsis, then coasted to apoapsis, where it performed a plane change, and then it arrived at periapsis, performing the manoeuvre described in this post.
Over the next few days the spacecraft should move into a reconnaissance orbit, which is given in Wikipedia to be a 265 x 60000 km orbit (having a period of 2 days) with an inclination of 86.9 degrees. However, the last burn hasn’t lowered the apoapsis that much. The current orbit is approximately 280 x 84600 km (3.45 day period) with an inclination of 87.7 degrees. A possible reason for using the current orbit, which has been described as a phasing orbit, will be explained in this post after reviewing the data we have about the burn.
Tianwen-1 plane change manoeuvre
Today at 9:00 UTC Tianwen-1 made its plane change manoeuvre, as reported by Xinhua. Yesterday I showed my planning for this manoeuvre. Shortly after the spacecraft returned to the high gain antenna after the manoeuvre, the Bochum 20m antenna operated by AMSAT-DL received state vectors with the new trajectory. These state vectors allow us to calculate the timestamp of the burn and the delta-V vector, as I have done in other occasions. It is convenient to remark that the state vectors that we are seeing right now are probably a prediction. In the next few days we will see updates in the trajectory as the Chinese DSN measures the effects of the actual burn and updates the onboard ephemerides.
Tianwen-1 plane change planning
Today, the Chinese media published a short piece of news stating that tomorrow, 2021-02-15, Tiawen-1 will make make a plane change to a polar orbit. The post is accompanied by an short video, which includes an animation depicting the manoeuvre. A screenshot of the video is shown below. As the spacecraft arrives to apoapsis, it effects a plane change into an ascending polar orbit.
This is a good moment to review the maths behind a plane change manoeuvre and compute what the manoeuvre will look like.
Tianwen-1 Mars-centric state vectors
Since launch, Tianwen-1 has transmitted as part of its telemetry some state vector data, giving its position and velocity vector every 32 seconds. This has allowed us to propagate, track and study its trajectory. We noticed the presence of the state vector data a few hours after launch, and since then we have received and decoded this data using the 20m antenna at Bochum observatory, which is operated by AMSAT-DL. This has allowed us to supply accurate orbit information to JPL HORIZONS, so that Amateur observers (and also some professional ones, for which Tianwen-1 is a useful and strong X-band beacon) can easily get ephemerides for the spacecraft.
Until now, the state vector data has encoded the spacecraft’s Cartesian position (in km) and velocity (in km/s) in a heliocentric reference frame. It is not completely clear if the frame is supposed to be ICRF or MJ2000, since the difference between the two is very small (see Section 3.5 in this paper by Kaplan) to be able to distinguish them with the data at hand, but we have always been using ICRF so far for consistency.
Today we have noticed that starting at some point on 2021-02-08, Tianwen-1 is now transmitting state vectors using a different, Mars-centric frame of reference. We don’t have the exact moment of the change. The last heliocentric vector we received was
2021-02-07 23:23:03.744100 18791639.655712113 211029173.8782428 96492674.05965108 -21.108400067542537 4.768376820024702 1.8445381918644286
This vector was received with one of the antennas at Allen Telescope Array, which I used as a backup since Bochum was unable to track that day due to a big snowfall.
The first Mars-centric state vector was received by Bochum the next day, and is
2021-02-08 22:14:25.049300 -345203.0840200648 103420.7793506239 -15761.456419116437 2.409386271990221 -0.7794198288828312 0.12118319008153547
The change in the frame of reference is clear from the change in magnitude of the position vector. Ensuring that the Mars-centric state vectors are interpreted correctly is important to continue using the data accurately. In this post I give the assessment of the appropriate reference system to use.
Tianwen-1 TCM-4
Today, 2021-02-05 at 12:00 UTC, Tianwen-1 has executed TCM-4. This is its last trajectory correction manoeuvre before the arrival to Mars orbit next Tuesday February 10. This was reported by Chinese media together with a black and white image of Mars taken recently by the spacecraft.
As usual, I have analysed this manoeuvre by propagating forwards the last state vector that we have from the spacecraft’s telemetry before the manoeuvre, propagating backwards the first state vector that we have after the manoeuvre, and finding the intersection point of the two trajectories.
Tianwen-1 TCM3 final trajectory
A few days ago I posted about TCM3, the fourth trajectory correction made by Tianwen-1 so far. After some days, the Chinese DSN has performed precise orbit determination and updated the on-board ephemerides, so that we are now seeing the final trajectory in the telemetry state vectors.
The figure below shows how the state vectors have been updated a couple of times following the TCM, as the DSN computes and uploads an improved trajectory solution. I have plotted this graph in the following way: I have taken the first state vector received after TCM3, on the UTC afternoon of 2020-10-28, and used it to propagate a trajectory in GMAT. The plot shows the difference between the state vectors and the GMAT trajectory.
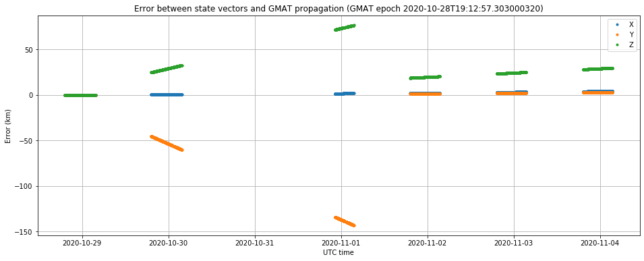
TCM3 happened on 2020-10-28 at 14:00 UTC, so the reference trajectory computed in GMAT corresponds to the trajectory of the state vectors immediately following the TCM. These are based on a prediction of the burn performance, rather than on the actual results. The graph above shows clearly two changes in the trajectory, one on 2020-10-29, and another one on 2020-11-01.
Since we have already seen the same trajectory for three days without updates, I am confident that this trajectory is now final. The latest state vector we have today is
[0163f5396aeb] 2020-11-04 03:25:57.092300 160383830.37880394 94290296.68475787 45404213.83552203 -9.17821106231485 22.96506090856966 10.332601544380973
As always, this gives the UTC timestamp and the ICRF heliocentric position and velocity coordinates in km and km/s respectively.
I have re-run the calculations in the previous post by back-propagating a state vector from the UTC evening of 2020-11-01, which already belongs to the final trajectory. The change in delta-V in comparison to what I should in the previous post is small. The new delta-V is 2.13 m/s rather than 2.09 m/s, and the components have changed around 5%. The detailed calculations and data can be found in the updated Jupyter notebook.
Tianwen-1 TCM3
On 2020-10-28 at 14:00 UTC, Tianwen-1 has made its third trajectory correction manoeuvre. This has been the next manoeuvre after the deep space manoeuvre at the beginning of October. According to the press release, this was a firing of the eight 25N thrusters intended as a minor correction and as a test of this propulsion system. I haven’t found the duration of the burn in the news.
I have followed the same method as in previous burns to compute the moment of the burn and the delta-V vector by extrapolating the telemetry orbit state vectors received by AMSAT-DL in Bochum before and after the burn. This extrapolation locates the burn at 14:02:28 UTC. Note that this time is an approximation for the mid-point of the burn.

The delta-V vector was, in m/s
[-0.6575566 , -0.11513034, 1.97535319],
and the magnitude was 2.09m/s. Assuming a mass of 5000kg and eight 25N thrusters, it would take a burn of 52 seconds to achieve this delta-V.
Update 2020-10-30: according to this news article, the duration of the burn was 42.8 seconds which is some 18% smaller than my estimate. Note that my estimate didn’t take into account the mass of fuel spent by the deep space manoeuvre, which I estimated to be 457kg (giving a decrease in mass of 9%).
Apparently this burn has lowered the periares height significantly in comparison to the trajectory following the deep space manoeuvre, which was around 18000km. Thanks to Achim Vollhardt for noticing this. It’s difficult for me to give a good estimate of the new periares height, because it is quite sensitive to orbit perturbations. I’ve obtained anything between 30 and 800 km by enabling and disabling solar radiation pressure in the GMAT propagator, and we don’t have a good estimate of the spacecraft’s cross-section and reflection coefficient.
The figure below shows one of the GMAT simulations. Note that the periares is near the equator, which is good for insertion into a low inclination orbit.
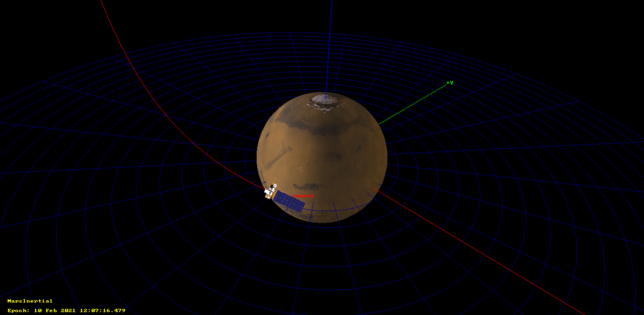
Keep in mind that according to the media still one more trajectory correction manoeuvre remains and that the data used in this post comes straight from the spacecraft’s telemetry, and as such is most likely based on a prediction of the burn rather than on the actual performance of the burn. In a few days, I will publish a new post when the Chinese DSN perform precise orbit determination and upload updated orbital information to the spacecraft.
The data and plots for this post can be found in this Jupyter notebook.
Tianwen-1 post–TCM-1 state vectors
Yesterday I reported about Tianwen-1’s first trajectory correction manoeuvre, TCM-1. In that post I commented the possibility that the updated state vectors that we saw on the telemetry after TCM-1 might come from a prediction or planning rather than take into account the actual performance of the burn.
The figure below shows the error between the state vectors collected after TCM-1 over the last two days, and a trajectory propagated in GMAT, using the following state vector, which is one of the first received after TCM-1.
[0151059eb9ea] 2020-08-02 00:17:06.711400 100230220.21360767 -106145016.11787066 -45441035.07405791 25.581827920522485 18.240707152437626 8.567874276424218
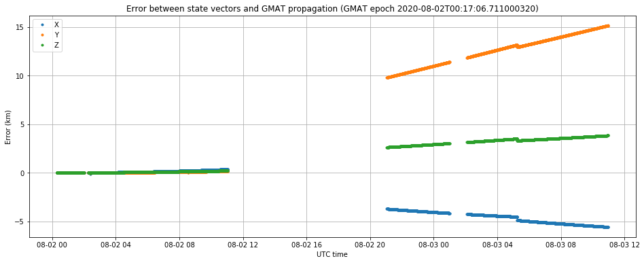
We see that on the UTC night between August 1 and 2 the state vectors deviate very little from the GMAT trajectory. However, on the UTC night between August 2 and 3 we see a slightly different trajectory in the state vectors. We have no data in between, as the spacecraft is not visible in Europe, so we don’t know the precise moment of change. The gap in telemetry around 2020-08-03 00:45 UTC is due to a transmission of high-speed data.
It seems reasonable to think that after TCM-1 the Chinese DSN performed precise ranging of the spacecraft to determine the new orbit accurately and then uploaded a correction to the state vectors on-board Tianwen-1.
The state vectors from last night all describe the same trajectory, as shown in the plot below which uses
[0151322e67d0] 2020-08-02 21:03:08.078400 102132184.96868199 -104770375.00352533 -44795830.46284772 25.29849580646669 18.532513218789806 8.692135086385246
to propagate a trajectory in GMAT. There is a small jump of a few hundred meters at some point. We usually see one or two these jumps per day, but we don’t understand well why they happen.
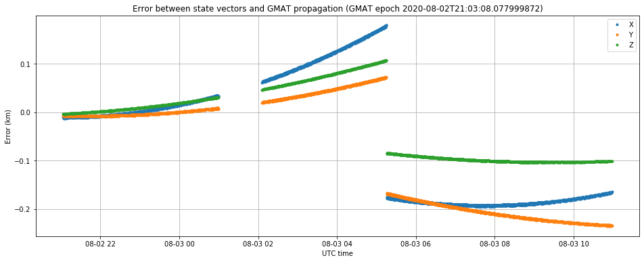
The trajectory according to the state vectors from 00:17:06 and from 21:03:08 are very similar. For example, at the closest approach to Mars they only differ in 1197km. For comparison, the difference between the new trajectory and the pre–TCM-1 trajectory is 126529km (again, at the closest approach to Mars).
I have generated a new table of right-ascension, declination and distance coordinates based on the updated state vectors. Note that this table doesn’t include light-time delay to the spacecraft.
Thanks to AMSAT-DL‘s Bochum observatory team and to Paul Marsh M0EYT for their continuous effort in tracking Tianwen-1. The data used in this post has come from their observations.