Since launch, Tianwen-1 has transmitted as part of its telemetry some state vector data, giving its position and velocity vector every 32 seconds. This has allowed us to propagate, track and study its trajectory. We noticed the presence of the state vector data a few hours after launch, and since then we have received and decoded this data using the 20m antenna at Bochum observatory, which is operated by AMSAT-DL. This has allowed us to supply accurate orbit information to JPL HORIZONS, so that Amateur observers (and also some professional ones, for which Tianwen-1 is a useful and strong X-band beacon) can easily get ephemerides for the spacecraft.
Until now, the state vector data has encoded the spacecraft’s Cartesian position (in km) and velocity (in km/s) in a heliocentric reference frame. It is not completely clear if the frame is supposed to be ICRF or MJ2000, since the difference between the two is very small (see Section 3.5 in this paper by Kaplan) to be able to distinguish them with the data at hand, but we have always been using ICRF so far for consistency.
Today we have noticed that starting at some point on 2021-02-08, Tianwen-1 is now transmitting state vectors using a different, Mars-centric frame of reference. We don’t have the exact moment of the change. The last heliocentric vector we received was
2021-02-07 23:23:03.744100 18791639.655712113 211029173.8782428 96492674.05965108 -21.108400067542537 4.768376820024702 1.8445381918644286
This vector was received with one of the antennas at Allen Telescope Array, which I used as a backup since Bochum was unable to track that day due to a big snowfall.
The first Mars-centric state vector was received by Bochum the next day, and is
2021-02-08 22:14:25.049300 -345203.0840200648 103420.7793506239 -15761.456419116437 2.409386271990221 -0.7794198288828312 0.12118319008153547
The change in the frame of reference is clear from the change in magnitude of the position vector. Ensuring that the Mars-centric state vectors are interpreted correctly is important to continue using the data accurately. In this post I give the assessment of the appropriate reference system to use.
The fact that this new frame of reference is Mars-centric is clear because the switch from heliocentric to Mars-centric is the obvious thing to do now that the spacecraft will soon enter Mars orbit, and because the magnitude of the vectors matches the spacecraft’s distance to Mars. The first candidate for the direction of the axes is ICRF. However, this doesn’t match.
Another good choice is what GMAT calls the “body intertial” frame (see Section 2.6.11 in GMAT’s Mathematical Specification). This frame uses a celestial body, Mars in this case, to define the axes. The z axis points along the spin axis of the body at the J2000 epoch. The x axis points along the intersection of the xy-plane of the FK5 system at the J2000 epoch. The y axis completes the right-handed system. The spin axis data comes from the paper “Report of the IAU/IAG Working Group on Cartographic Coordinates and Rotational Elements of the Planets and Satellites: 2000” (behind paywall), which is revised every three years (see for instance the version for 2006).
The GMAT body inertial frame of reference gives a match for the Mars-centric state vectors transmitted by Tianwen-1, but the match is not particularly good, since the positional error is around 100 km. In what follows I assess whether it is reasonable to use the GMAT Mars body inertial frame to work the state vectors.
The idea in this small study is to take a state vector transmitted by the spacecraft (TM state vector), propagate it in GMAT to give a position track in a certain coordinate system, interpolate the positions in that track to the timestamps of a series of TM state vectors, and compute and plot the difference in positions. The first comparison that we do is to take the first TM vector received by ATA on 2021-02-07, propagate it, and compare it with all the state vectors received by ATA during that observation. The difference is shown below.

This plot is quite reasonable. Since the observation is short, we see differences of a few metres, caused by time quantization and by the fact that the GMAT and the spacecraft propagators are not exactly the same. We see two discrete jumps in the TM state vectors slightly before 22:30 UTC. These are common, and we don’t know exactly what causes them.
It is important to note that here the difference is particularly small because the observation only lasts 2 hours and 30 minutes. When propagating from day to day it is normal to see an error building up to a few km, specially after a manoeuvre, as the Chinese DSN perform orbit determination and compute and upload updated vectors to the spacecraft (see this post that describes what happened after TCM-3). Keep in mind that TCM-4 happened only a few days ago.
Next we take the same propagated trajectory (which uses a Sun-centric state vector as seed), make GMAT output Mars body inertial coordinates, and compare those with the TM state vectors received by Bochum on 2021-02-08. The results are below. The position difference is 136 km, which requires us to be careful before giving the body inertial interpretation as valid.
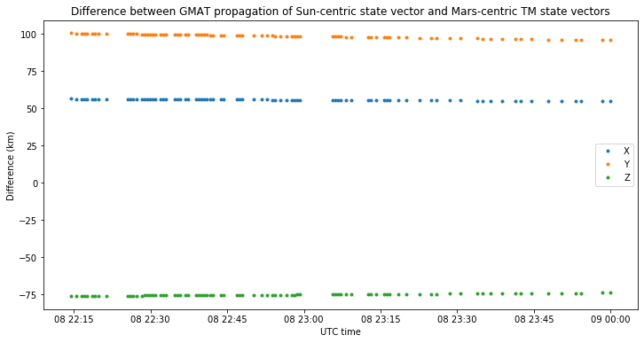
Since the change in the difference cannot be seen due to the scale of the plot, it is a good idea to remove the average and plot again. Now we see that even though the overall position is 136 km wrong, the “shape” of the trajectory only differs by a couple km.
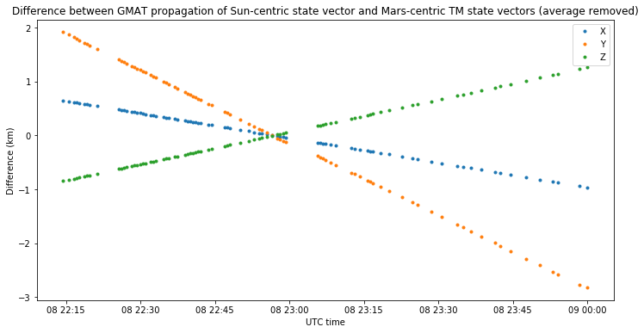
The position error may be caused by a number of factors. First of, the difference between ICRF and MJ2000 coordinates (around 16 milliarcseconds), as seen from the Sun at the distance of Mars is on the order of 15 km. Second, different versions of the JPL DE planetary ephemerides may give slightly different positions for the Mars barycenter, though I am not sure about the magnitude of the differences. GMAT R2020a is using DE405, which dates back to 1997. Finally, we have the uncertainty in Tianwen-1’s orbit itself, since TCM-4 was performed a few days ago, so the orbit solution transmitted by the spacecraft is not final and may jump several tens of km.
In any case, it is pretty clear that the centre of the reference system is Mars barycenter (what other point that is at some 100 km from the Mars barycentre could it be?). Once the spacecraft is inside Mars Hill sphere, fundamentally we only care about the position of the spacecraft with respect to Mars barycenter in order to propagate its orbit. The directions of the coordinate axes are not so important. They only come into play when computing perturbations, such as the forces of other bodies in the solar system, or the effect of Mars non-spherical gravity field, or when checking if the spacecraft is behind Mars, as seen from Earth. As such, it is desirable to get the directions of the coordinate axes right, but a small error is not very noticeable.
A position error of 136 km, at the spacecraft’s distance to Mars, represents an angular movement of only 0.02 degrees. Therefore, even if the state vectors used a slightly different definition for the Mars spin axis, or for the direction of the x axis, the difference would be a small rotation.
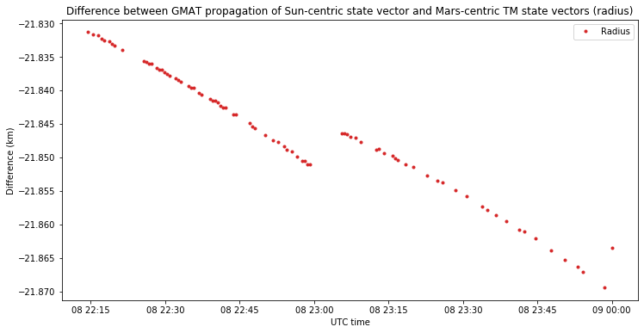
Following this way of thinking, we separate the position error into a radial difference (the difference of the magnitudes of the vectors) and an angular difference (the angle between the vectors). The radial difference is shown below. It’s only 21.8 km.
The angle difference is around 0.021 degrees.
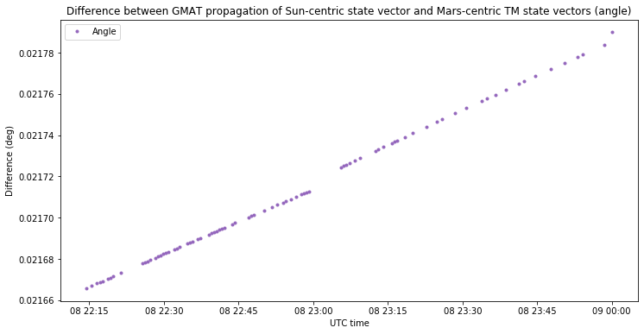
Therefore, my conclusion is that it is reasonable and acceptable to use these new Mars-centric state vectors with the Mars body inertial reference frame in GMAT. As a sanity check, we take the first of these Mars-centric vectors, propagate it in GMAT, and compute the difference between the GMAT track and the Mars-centric TM state vectors. The result is shown here.
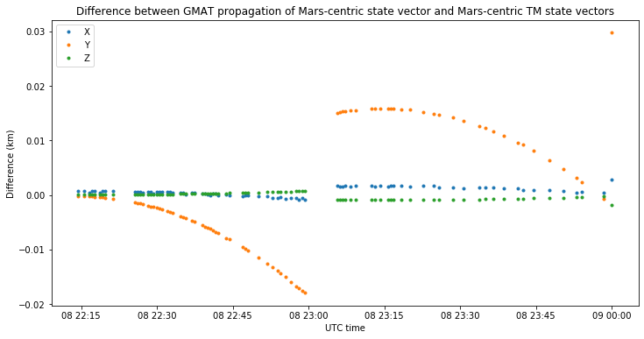
The difference is very small, of a few metres. There is something a bit weird going on with the Y variable, but since we see jumps in the spacecraft’s TM vector track, this suggests that the very small problem is with the TM vectors themselves, and not with the GMAT track diverging.
The Jupyter notebook where these calculations and plots have been made can be found here, together with the supporting data.
Spacecraft have been orbiting Mars since 1976, so I assume we have a very good model of Mars’ gravity field by now? We didn’t have a good one of our Moon until fairly recently (GRAIL) but that was probably a special case because of its tidal locking.
Hi Phil, that’s a very good question. I don’t know much about state-of-the-art gravity models for Mars. Now I wonder to what extent the distance to Mars makes precise orbit determination more difficult, impacting our ability to derive a good gravity field model.
All I can say is that GMAT, which is what I’m using for orbit propagation, ships with three models: Mars50c, GMM-1 and GMM-2B, and that I’m currently using a 10×10 subset of Mars50c (which is the default model). This seems good enough for propagating the orbit accurately for several days. In fact, for this high elliptical orbit the spacecraft is quite far from the planet, so that only the first few spherical harmonic coefficients would matter (except perhaps when passing periapsis).
An interesting experiment would be to wait until the spacecraft is on its remote sensing orbit (a circular polar orbit), gather state vector data for several days or weeks, and then compare the state vector trajectory with propagation using different gravity models and numbers of coefficients.