Last Thursday 2020-07-23 at 04:41 UTC, Tianwen-1, a Chinese mission to Mars consisting of an orbiter, a lander and a rover, launched from Wenchang. Usually, I would be posting an analysis of a recording of the telemetry signal, made by Paul Marsh M0EYT or another of my Amateur DSN contributors, as I did a few days ago for the Emirates Mars Mission. However, something amazing has happened that has kept me quite busy. Rest assured that the analysis of the signal will come in a future post, but here I’m going to tell a story about Tianwen-1’s orbit.
The Chinese DSN hasn’t published orbit information for Tianwen-1, making it difficult both for Amateurs and for other space agencies to track the spacecraft. In fact, Richard Stephenson from NASA DSN was wondering on Twitter if ESA was collaborating with the Chinese, and a bit of mystery has surrounded this mission, since people can’t go to NASA Horizons to get the spacecraft ephemerides as they’re used to.
Finding the signal shortly after launch is perhaps not so difficult. The signal is strong when the spacecraft is close to Earth, and since downlink frequencies are known, the spacecraft can be found just by searching with a small antenna. Once the spacecraft gets further from Earth, finding it is not so easy. Its signal will be weaker, and it will change its position in the sky from day to day, so that trying to find it without knowing where to look can be like finding a needle in a haystack.
As usual, Paul was able to make several recordings of X-band telemetry downlink shortly after launch, starting at 06:26 UTC, and other people such as Edgar Kaiser DF2MZ also received the spacecraft’s signal. However, before I could have a chance to look at these recordings, Paul contacted me on Thursday afternoon about a seemingly unrelated topic. He was asking about star trackers and what does their data typically look like. I mentioned quaternions and rotation matrices, showed Paul the star tracker telemetry from Longjiang-2 and suggested a look at openstartracker for further info.
Then Paul sent me these numbers and asked if they looked like they could be star tracker data of some sort. He also told me to keep this secret for now.
start at 20200723 064007z 77395324.623705 -120028596.942956 -52029631.885987 31.179136 15.128088 7.490056 77396322.143351 -120028112.790527 -52029392.206920 31.164092 15.130745 7.489563 77397319.187608 -120027628.552638 -52029152.543120 31.149230 15.133334 7.489055 77398315.752926 -120027144.235999 -52028912.897277 31.134548 15.135857 7.488534 77399311.882344 -120026659.824552 -52028673.260826 31.120041 15.138314 7.488001 77400307.522297 -120026175.349102 -52028433.648397 31.105707 15.140709 7.487454 77401302.706282 -120025690.798014 -52028194.053632 31.091543 15.143042 7.486897 77402297.436567 -120025206.174733 -52027954.477645 31.077545 15.145315 7.486328 77403291.727750 -120024721.476590 -52027714.918538 31.063711 15.147531 7.485748 77404285.603633 -120024236.696317 -52027475.372151 31.050037 15.149691 7.485159 77405279.016507 -120023751.861438 -52027235.851524 31.036520 15.151797 7.484559 77406271.999323 -120023266.960042 -52026996.350220 31.023158 15.153849 7.483951 77407264.556986 -120022781.993803 -52026756.868523 31.009948 15.155849 7.483334 77408256.694314 -120022296.964349 -52026517.406704 30.996887 15.157800 7.482709 77409248.443923 -120021811.859618 -52026277.958286 30.983973 15.159702 7.482076 77410239.751582 -120021326.709953 -52026038.537730 30.971202 15.161556 7.481435 77411230.659047 -120020841.498660 -52025799.136289 30.958574 15.163364 7.480788 77412221.158421 -120020356.233262 -52025559.757174 30.946084 15.165127 7.480133 77413211.266493 -120019870.909112 -52025320.397602 30.933731 15.166847 7.479473 77414201.006145 -120019385.518485 -52025081.053283 30.921512 15.168524 7.478806 77415190.329062 -120018900.088512 -52024841.737118 30.909425 15.170159 7.478134 77416179.267271 -120018414.606850 -52024602.442550 30.897468 15.171754 7.477456
I told him that I didn’t think so, since those numbers had 6 values per data point, while a star tracker would usually have 3 or 4, and the values didn’t look like angles or rotation quaternions.
However, on a second look I noticed that the first three values had more or less the same order of magnitude (and it was large indeed), and the second three values had the same much smaller order of magnitude. This reminded me a little of Cartesian state vectors, which we had used extensively in the Longjiang-2 mission to the point where I now have a folder filled with hundreds of MBs of this kind of data. I told Paul to hold on a second while I checked something.
A Cartesian state vector indicates the position and velocity of a spacecraft at a given instant. Since we can know all the forces acting on a spacecraft (mainly gravity, but also others), this is all the data we need to propagate the spacecraft’s trajectory. Cartesian state vectors are given either in km and km/s or in m and m/s, and as you can imagine, the position vector is often huge, while the velocity is not so large.
To check if these numbers could be a Cartesian state vector, I subtracted the first three numbers from the first couple of rows (which presumably were the positions), then divided the result by the second three numbers in the first row (presumably the velocity). The result was that the difference in positions was pretty close to 32 times the velocity. The same happened for all the data in the table, so my conclusion is that this was indeed Cartesian state vectors spaced 32 seconds apart.
I told Paul that I was pretty sure that this was no star tracker data, but Cartesian state vectors of some sort. He said that it would be great to know where the object in question was. I told him that perhaps that wouldn’t be too difficult, since to define a Cartesian state vector we only need a frame of reference, which consists of an origin that is usually placed on a celestial body, such as the Earth, the Sun or the Solar system barycentre (SSB), and directions for the coordinate axes. Since there are only a few usual choices, from the appearance of the numbers and some context it might be possible to guess the frame of reference.
I computed the magnitude of the position vector, and assuming the units where km I obtained 1.05 AU. This made me suspect that the origin was either the Sun or the SSB and the object was something close to Earth. Paul was following along with interest and telling me that indeed it should be close to Earth. To check if the object was in fact close to Earth, I needed to compute the Earth’s coordinates in this reference system.
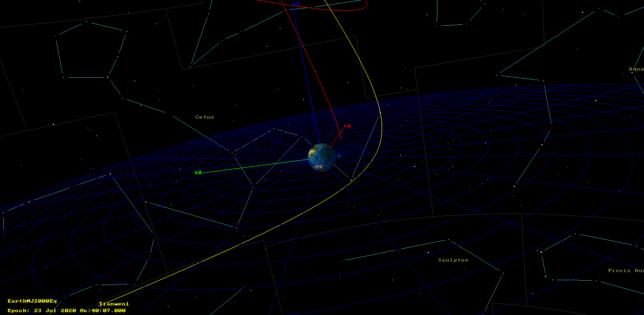
I was tempted to do it in Astropy, but decided to fire up GMAT instead, as I could also propagate the object’s orbit and get pretty pictures. My first try was to interpret the data as SSB ICRF coordinates. As shown below (click to view in full size), I got an object that started near Earth and went off to Mars, but not quite reached it.
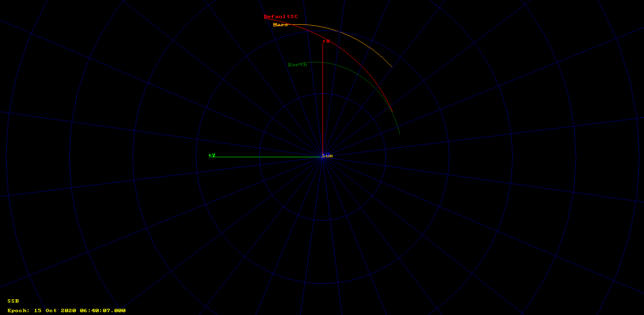
I tried other axes to see if they worked better. GMAT’s documentation webserver was down, so that wasn’t helping. By using the TODEq axes (which in fact I had never used before), I got something that started off 200000km away from Earth, which didn’t seem so bad. Still, the orbit was not right to reach Mars.
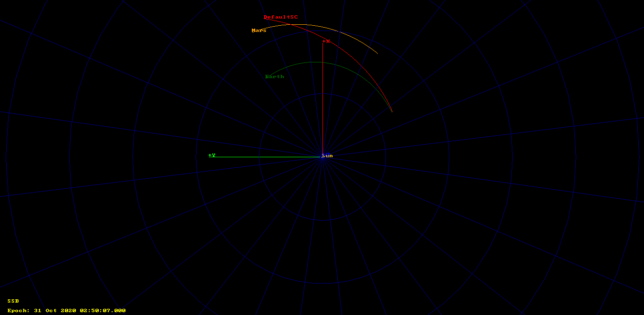
Paul also told me that 200000km seemed too far, since the object had been launched at 04:41 UTC. At some point I realised that the discussion had shifted from hypothetical star tracker questions to the actual orbit of Tianwen-1.
Then it occurred to me to try using the Sun as the origin instead of the SSB. This gave much better results. I got a trajectory that started off 29311 km away from Earth and arrived near Mars on 2021-01-24.
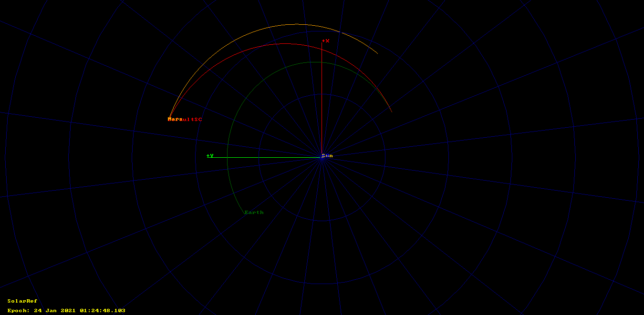
So all this seemed quite reasonable, but Paul still wanted us to check this orbit against the antenna pointing he used when tracking Tianwen-1 that Thursday morning. I generated azimuth/elevation data for his station with GMAT, and it turned out that it matched alright the antenna pointing.
Then Paul told me what I still find most amazing about this story: the Cartesian state data had come from the telemetry of the spacecraft itself. It turned out that r00t.cz had also been working with Paul’s recordings and managed to pull out from the telemetry frames the table of numbers I’ve listed above. r00t and Paul didn’t understand well the nature of this data, but for some reason they thought it might be related to the spacecraft’s trajectory.
Let me give some context for why I find this amazing. First, as you can see on some of my other posts about deep space probes, we can often find the modulation and FEC, and decode the frame headers (since they use CCSDS standards), but then we look at the contents of the frames and find ourselves lost, not knowing anything about what kind of data is transmitted, or which format is used to encode the data. So often we don’t get much further than that.
Now that we know what kind of numbers to look for, it’s not so difficult to find them in the telemetry frames, and in fact I’ll show all the details in a future post, but without knowing what to look for, it’s a daunting task. If I was checking these frames, I would probably get bored and move to another project before finding the state vector data. So I think that what r00t did is very impressive and would love hearing his story about how he noticed the presence of the state vector data in the telemetry frames.
Second, from what we can tell, the spacecraft continuously transmits its own real time state vector every 32 seconds. This is weird. The spacecraft’s state vector is estimated on ground by the Chinese DSN using ranging measurements. The spacecraft needs to know its own trajectory, in order to point its antennas to Earth, for example, but I guess that the spacecraft is preloaded with a predicted mission profile, and then this onboard data is updated by the DSN if necessary. The DSN might even need to check the validity of the onboard orbit data, and so might ask the spacecraft to downlink a copy of this data. But I can’t think of a reason to downlink this data continuously.
In any case, Paul and I made azimuth/elevation and right ascension/declination pointing data and distributed it to a few Amateur DSN stations. This would validate the orbit if they were able to find the spacecraft’s signal next morning using this pointing data.
On Friday, I spent most of the day away from home, so I couldn’t work with the orbit data. Edgar reported that our pointing data worked more or less fine, but was a few degrees off, so I planned to spend my Saturday assessing the quality of the orbit data, a task which Edgar made easier by taking care to collect pointing data from several Amateur stations.
On Saturday morning, Achim Volhardt DH2VA, James Miller G3RUH and the rest of the Bochum observatory team managed to use the 20m antenna at the observatory to track the spacecraft and perform a few recordings. The full story that shows the capabilities of Amateur radio operators to track deep space missions can be read in this news piece at AMSAT-DL.
The 20m antenna has a beamwidth of 0.1 degrees at X-band, so it is able to give much more accurate pointing data than the Amateur stations with smaller dishes. Therefore, the pointing data collected by Bochum would be very valuable to assess the orbit quality, since Achim also reported that he needed to tweak the pointing a few degrees.
During Saturday morning, r00t.cz and Paul were able to decode updated state vectors from the spacecraft’s telemetry. These are shown below.
[ 335 07:44:02.217 ] [ 335 07:44:00.558 ] = 82339427.525020 -117411231.235495 -50765981.325446 27.983074 15.464298 7.384547 [ 335 07:44:34.218 ] [ 335 07:44:32.559 ] = 82340322.999380 -117410736.368200 -50765745.015509 27.982950 15.464434 7.384601 [ 335 07:45:06.218 ] [ 335 07:45:04.560 ] = 82341218.489344 -117410241.485726 -50765508.698670 27.982825 15.464570 7.384655 [ 335 07:45:38.218 ] [ 335 07:45:36.560 ] = 82342113.952936 -117409746.611268 -50765272.386007 27.982701 15.464706 7.384709 [ 335 07:46:10.218 ] [ 335 07:46:08.561 ] = 82343009.409746 -117409251.734003 -50765036.072349 27.982576 15.464842 7.384763 [ 335 07:46:42.218 ] [ 335 07:46:40.561 ] = 82343904.870966 -117408756.847743 -50764799.754744 27.982452 15.464978 7.384817 [ 335 07:47:14.218 ] [ 335 07:47:12.562 ] = 82344800.322605 -117408261.960221 -50764563.436883 27.982327 15.465114 7.384872 [ 335 09:06:42.230 ] [ 335 09:06:40.662 ] = 82478178.937139 -117334474.639337 -50729332.489742 27.963857 15.485400 7.392959 [ 335 09:07:14.230 ] [ 335 09:07:12.663 ] = 82479073.796377 -117333979.096727 -50729095.910577 27.963733 15.485536 7.393013 [ 335 09:07:46.230 ] [ 335 09:07:44.664 ] = 82479968.671237 -117333483.538917 -50728859.324496 27.963610 15.485672 7.393068 [ 335 09:08:18.231 ] [ 335 09:08:16.665 ] = 82480863.519773 -117332987.989137 -50728622.742587 27.963486 15.485809 7.393122 [ 335 09:08:50.231 ] [ 335 09:08:48.665 ] = 82481758.364358 -117332492.434998 -50728386.158936 27.963363 15.485945 7.393177
I think that a story is never a complete success story. It always gives rise to questions or challenges. In this case, unfortunately the state vectors from Thursday (which I will call set1) and Saturday (which I will call set2) don’t match very well together.
To validate the consistency of each set of state vectors, and also to check if the timestamps are correctly calculated (which was one of my doubts), I have made a GMAT script that propagates from the first epoch in the set to the last one and checks the position error. I get small errors of around 1km. Especially in set1, if I change the timestamp slightly, the relative positions of Tianwen-1 and Earth change, which affects the orbit importantly, and produces a much larger error. Therefore, I am confident that we are assigning the timestamps correctly.
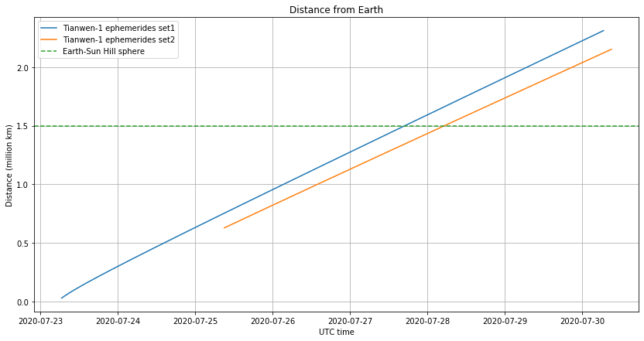
The distance between Tianwen-1 and Earth, as described by both ephemerides sets, is shown below. Here we can clearly see that the trajectories are noticeably different.
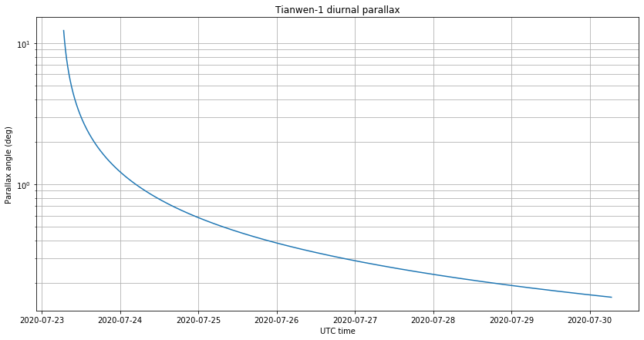
Regarding the distance from Earth, a word of caution is in order. Until the spacecraft is far enough from Earth, the location of a groundstation on Earth affects the pointing, so that right ascension and declination data can’t be used directly and need to be corrected. The maximum magnitude of this effect, called diurnal parallax, is shown below.
Smaller stations can start using right ascension and declination on Saturday 2020-07-25, since the parallax is already less than one degree. However, for accurate pointing of a large antenna such as Bochum’s, the parallax is still noticeable one week after launch.
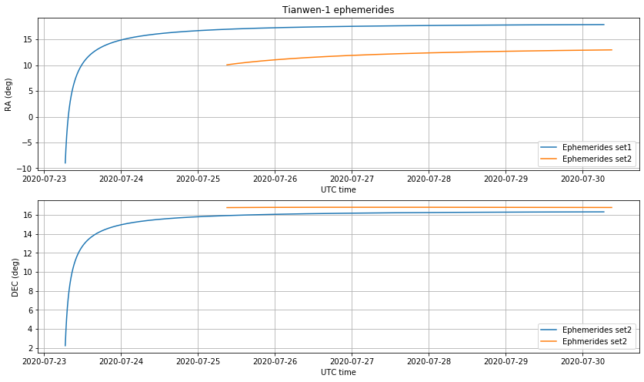
Below we show the right ascension and declination data for both sets of ephemerides. The declination is somewhat similar, but there is a large difference of around 5 degrees in right ascension.
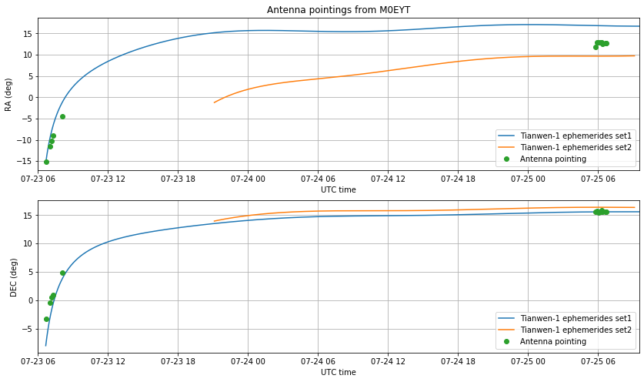
The figure below compares the antenna pointings measured at Bochum with the ephemerides sets, accounting correctly for parallax. We see that none of the sets is very accurate for right-ascension. Set1 has too large right ascension, while set2 has too small right ascension.

Using the data kindly collected and provided by Edgar, I have also compared the pointing data obtained by smaller Amateur stations. This is shown in the figures below. Note the small ripple, especially in the right ascension. This is due to the correction for parallax. The true right ascension is monotonically increasing, as shown above.
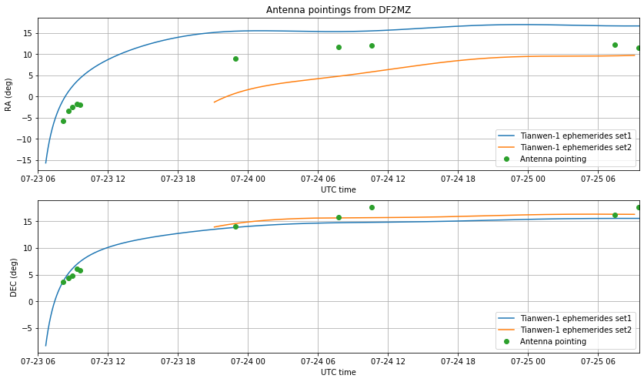
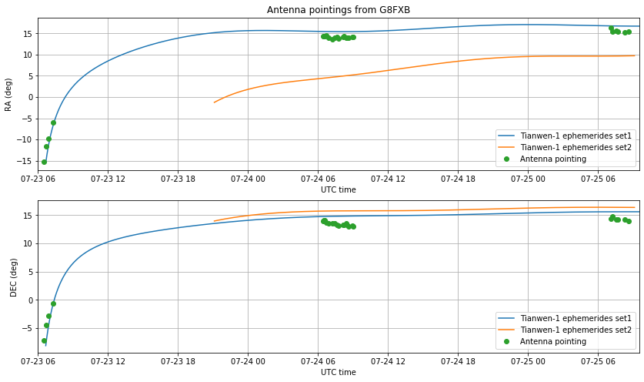
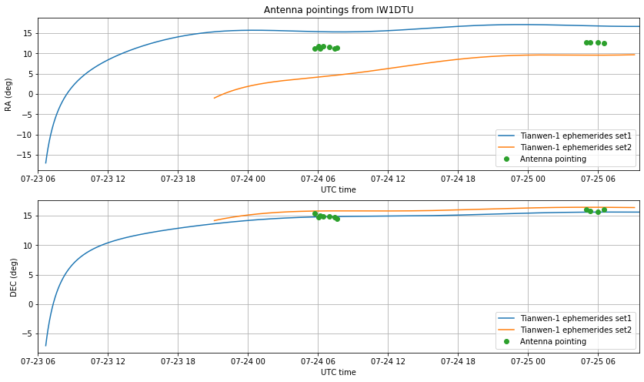
The data of all the stations is consistent with the measurements done at Bochum. The declination is more or less OK, but there is a problem in the right ascension. It also seems that set1 was OK right after launch, but then deviated significantly from the measurements.
I don’t have an explanation for these discrepancies. I am not sure that my interpretation of the the state vectors as being heliocentric ICRF coordinates is correct, but I have spent hours playing with other reference systems, and even making my own via small rotations of ICRF, and I can’t get anything that matches the observations better.
The comparison between the ephemerides and the observations has been made using this Jupyter notebook and this GMAT script.
The trajectory described by the two ephemerides sets starts off similar, but the diverges significantly, as shown in the figure below, where set1 is depicted in red and set2 in yellow.
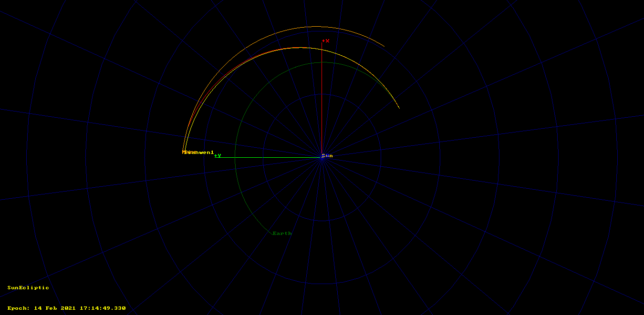
Set1 starts off 29311km away from Earth and gets within 1.25 million km of Mars on 2021-01-24, while set2 arrives within 3.7 million of km on 2021-02-14. Moreover, if we propagate backwards in time set2 to the epoch of set1, we see that their tracks are more or less parallel but set2 swings by past the Earth, which is impossible unless some manoeuvre was made after the epoch of set1.
The figures above have been obtained with this GMAT script.
Maybe it is worth to keep collecting telemetry from Tianwen-1 over the next few days, to study how the state vector transmitted by the spacecraft keeps changing. This might help us understand the data better. Still, all these inconsistencies might be explained by an appropriate choice of the reference frame and epochs, but so far I don’t see how.
Hello I may have photographed a plume from the departing spacecraft. Perhaps this ’round cloud’ I saw can be correlated with the known path of the departing Chinese probe.