10ghz – Daniel Estévez

Measuring the QO-100 beacons phase difference

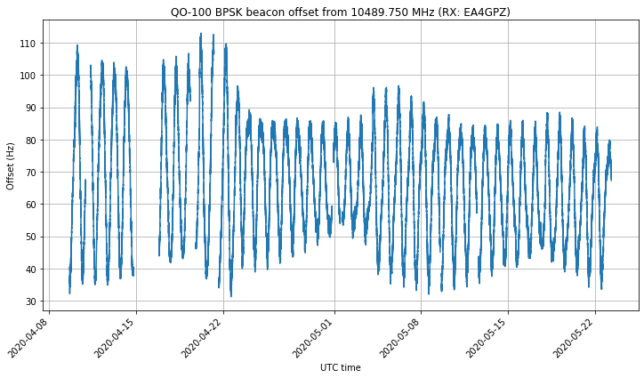
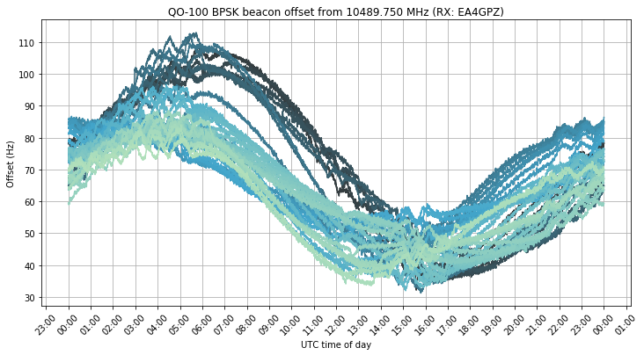
Since a couple months ago, the QO-100 NB transponder has now two digital beacons being transmitted continuously: the “traditional” 400 baud BPSK beacon, and the new 2.4 kbaud 8APSK multimedia beacon. This transponder is an amateur radio bent-pipe linear transponder on board the Es’hail 2 GEO satellite. It has an uplink at 2400.25 MHz, a downlink at 10489.75 MHz, and 500 kHz bandwidth. The two beacons are transmitted from the AMSAT-DL groundstation in Bochum, Germany, with a nominal frequency separation of 245 kHz.

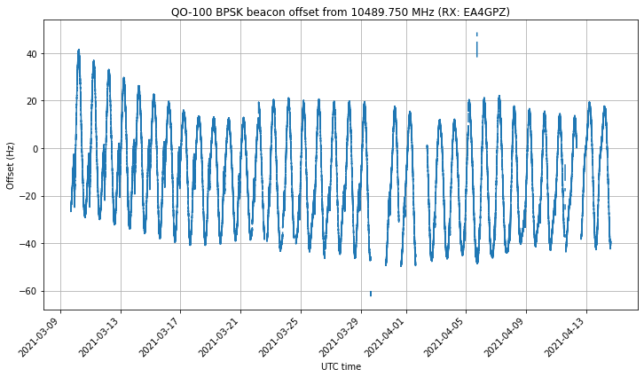
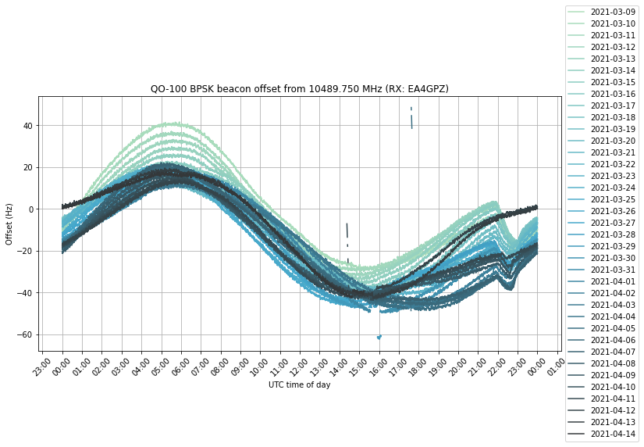
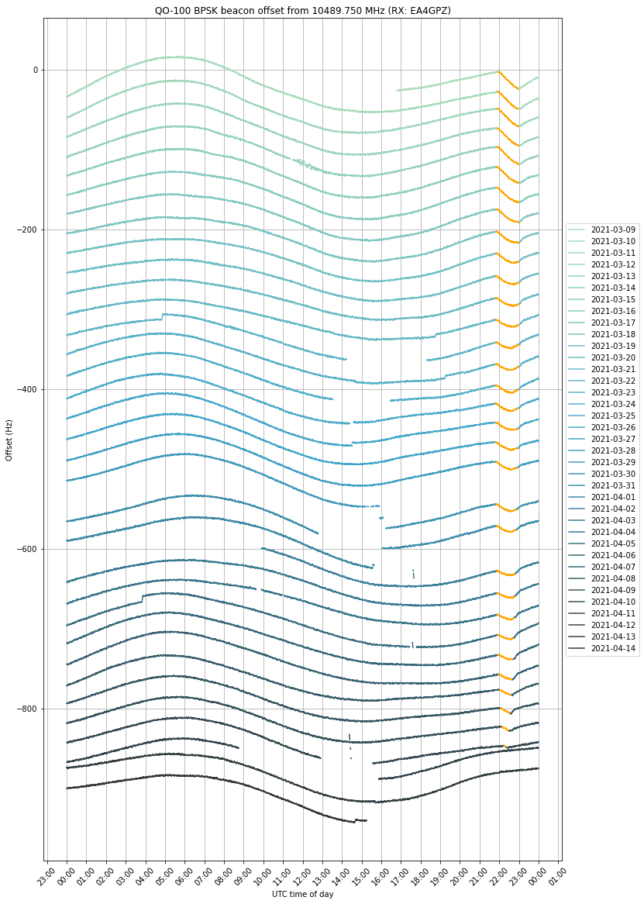
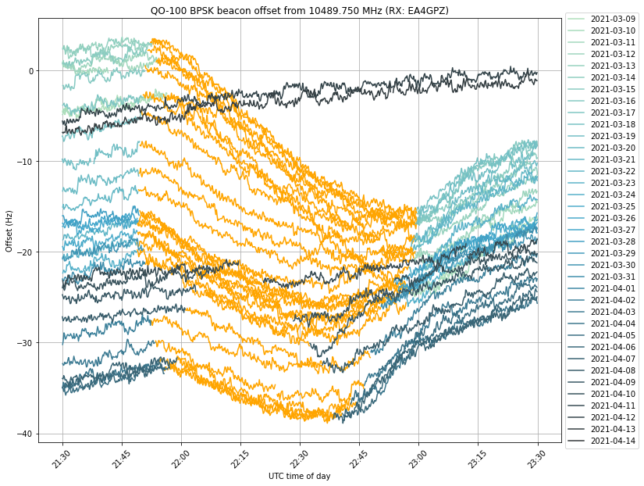
In some posts in the last few years (see this, for instance), I have been measuring the frequency of the BPSK beacon as received by my grounstation in Madrid, Spain. In these frequency measurements we can see the daily Doppler curve of the satellite, which is not completely stationary with respect to the surface of Earth. However, we can also see the frequency variations of the local oscillator of the transponder (including some weird effects called “the wiggles“). For this reason, the frequency of the BPSK beacon is not an ideal measurement for orbit determination, since it is contaminated by the onboard local oscillator.

If we measure the frequency (or phase) of the 8APSK and BPSK beacons and subtract the two measurements, the effects caused by the transponder local oscillator cancel out. The two beacons have slightly different Doppler, because they are not at the same frequency. The quantity that remains after the subtraction is only affected by the movement of the satellite.

Bochum and my station use both references locked to GPS. Therefore, the phase difference of the two beacons gives the group delay from Bochum through the transponder to my station. This indicates the propagation time of the signal, which is often known as three-way range. The three-way range is roughly the sum of distances between the satellite and each groundstation (roughly, but not exactly, due to the light-time delay). It is a quantity that is directly applicable in orbit determination.

In this post I present my first results measuring the phase difference of the beacons and the three-way range.

Rain backscatter on 10 GHz

Yesterday we had a strong storm in Madrid at around 16:30 UTC. The storm was rather short but intense. Seeing the heavy rain, it occurred to me that I might be able to receive the 10 GHz beacon ED4YAE at Alto del León using my QO-100 groundstation (without moving the antenna).

The 10 GHz beacon is 39.4 km away and the direct path to my station is obstructed by some hill in the middle, as shown in the link profile.

Link profile ED4YAE -> EA4GPZ (from HeyWhatsThat.com)

In the countryside just outside town it is possible to receive the beacon, probably because it diffracts on the hills. However, it is impossible for me to receive it directly from home, as there are too many tall buildings in the way.

In fact, when I fired up my receiver as the storm raged, I was able to see the beacon signal, with a huge Doppler spread of some 700 Hz (20 m/s). The CW ID of the beacon was easy to copy.

ED4YAE -> EA4GPZ at 10 GHz via rain backscatter

Then I started recording the signal. As the rain got weaker, it started disappearing, until it faded away completely. This post is a short analysis of the scatter geometry and the recording.

QO-100 spring eclipse season

A few days ago, the spring eclipse season for Es’hail 2 finished. I’ve been recording the frequency of the NB transponder BPSK beacon almost 24/7 since March 9 for this eclipse season. In the frequency data, we can see that, as the spacecraft enters the Earth shadow, there is a drop in the local oscillator frequency of the transponder. This is caused by a temperature change in the on-board frequency reference. When the satellite exits the Earth shadow again, the local oscillator frequency comes back up again.

The measurement setup I’ve used for this is the same that I used to measure the local oscillator “wiggles” a year ago. It is noteworthy that these wiggles have completely disappeared at some point later in 2020 or in the beginning of 2021. I can’t tell exactly when, since I haven’t been monitoring the beacon frequency (but other people may have been and could know this).

A Costas loop is used to lock to the BPSK beacon frequency and output phase measurements at a rate of 100 Hz. These are later processed in a Jupyter notebook to obtain frequency measurements with an averaging time of 10 seconds. Some very simple flagging of bad data (caused by PLL unlocks) is done by dropping points for which the derivative exceeds a certain threshold. This simple technique still leaves a few bad points undetected, but the main goal of it is to improve the quality of the plots.

The figure below shows the full time series of frequency measurements. Here we can see the daily sinusoidal Doppler pattern, and long term effects both in the orbit and in the local oscillator frequency.

If we plot all the days on top of each other, we get the following. The effect of the eclipse can be clearly seen between 22:00 and 23:00 UTC.

By adding an artificial vertical offset to each of the traces, we can prevent them from lying on top of each other. We have coloured in orange the measurements taken when the satellite was in eclipse. The eclipse can be seen getting shorter towards mid-April and eventually disappearing.

We see that the frequency drop starts exactly as soon as the eclipse starts. In many days, the drop ends at the same time as the eclipse, but in other days the drop ends earlier and we can see that the orange curve starts to increase again near the end of the eclipse. This can be seen better in the next figure, which shows a zoom to the time interval when the eclipse happens, and doesn’t apply a vertical offset to each trace. I don’t have an explanation for this increase in frequency before the end of the eclipse.

The plots in this post have been done in this Jupyter notebook. The frequency measurements have been stored in this netCDF4 file, which can be loaded with xarray.

Update on the QO-100 local oscillator wiggles

This post is a follow up to my study of the “wiggles” observed in the local oscillator of the QO-100 NB transponder. After writing that post, I have continued measuring the frequency of the BPSK beacon with my station almost without interruptions. Now I have some 44 days of measurements, spanning from April 9 to May 23. This data can be interesting to look at, so I’m doing this short post to share the data and look at it briefly.

The Jupyter notebook with all the data can be found here. The data is also linked in my jupyter_notebooks Github repository, which now uses git-annex to store the data in my home server. See the README for instructions on how to download some or all of the data files in the repository.

The whole time series can be seen in the figure below. We note that the typical Doppler sinusoidal curve varies slowly due to orbit perturbations and sometimes suddenly as a consequence of a station-keeping manoeuvre. I tweeted about one of the manoeuvres a while back.

There are now too many days in order to see things clearly when the frequency curves for each day are overlaid, but hopefully the figure below gives a good idea. We can see that the wiggles still happen approximately between 21:00 and 06:00 UTC, and between 11:00 and 17:00 UTC.

If we add an artificial offset of -15 Hz per day to the curves to prevent them from overlapping, we obtain the figure below. We see that the pattern of the wiggles keeps changing slightly, but also remains quite similar.

In my last post about this topic I said that it seemed that the wiggles repeated with a period of a sidereal day. Now it is clear that it is not the case. The wiggles seem to repeat roughly with a period of a solar day (24 hours). In fact, in 44 days sidereal time “advances” 2.88 hours with respect to solar time. However, it is clear that the wiggles haven’t shifted that much in time.

Wiggles in the QO-100 local oscillator

Some days ago, Hans Hartfuss DL2MDQ sent me an email about some frequency measurements of the QO-100 NB transponder BPSK beacon that he had been doing. The BPSK beacon is uplinked from Bochum (Germany) through the transponder, and as the beacon is generated using a very good Z3081A GPSDO as a reference, the frequency drift observed on the beacon downlink is caused by Doppler and the drift of the local oscillator of the transponder.

In his measurements, Hans observed some small oscillations or “wiggles” that didn’t seem to be caused by Doppler. Decided to investigate this, I started to do some measurements of my own. This post is an account of my measurements and findings so far.

Coherence and QO-100

My tweet about the AMSAT-BR QO-100 FT8 QRPp experiment has spawned a very interesting discussion with Phil Karn KA9Q, Marcus Müller and others about weak signal modes specifically designed for the QO-100 communications channel, which is AWGN albeit with some frequency drift (mainly due to the imperfect reference clocks used in the typical groundstations).

Roughly speaking, the conversation shifted from noting that FT8 is not so efficient in terms of EbN0 to the idea of using something like coherent BPSK with \(r=1/6\) CCSDS Turbo code, then to observing that maybe there was not enough SNR for a Costas loop to work, so a residual carrier should be used, and eventually to asking whether a residual carrier would work at all.

There are several different problems that can be framed in this context. For me, the most interesting and difficult one is how to transmit some data with the least CN0 possible. In an ideal world, you can always manage to transmit a weaker signal just by transmitting slower (thus maintaining the Eb/N0 constant). In the real world, however, there are some time-varying physical parameters of the signal that the receiver needs to track (be it phase, frequency, clock synchronization, etc.). In order to detect and track these parameters, some minimum signal power is needed at the receiver.

This means that, in practice, depending on the physical channel in question, there is a lower CN0 limit at which communication on that channel can be achieved. In many situations, designing a system that tries to approach to that limit is a hard and interesting question.

Another problem that can be posed is how to transmit some data with the least Eb/N0 possible, thus approaching the Shannon capacity of the channel. However, the people doing DVB-S2 over the wideband transponder are not doing it so bad at all in this respect. Indeed, by transmitting faster (and increasing power, to keep the Eb/N0 reasonable), the frequency drift problems become completely manageable.

In any case, if we’re going to discuss about these questions, it is important to characterize the typical frequency drift of signals through the QO-100 transponder. This post contains some brief experiments about this.

QO-100 BPSK beacon frequency measured at Bochum

The experiments about measuring the frequency stability of the local oscillator of the QO-100 NB transponder with a Vectron MD-011 GPSDO I made a few days ago indicated that the Allan deviation of the local oscillator was probably better than \(10^{-11}\) for \(\tau\) between 1 and 100 seconds. The next step in trying to characterize the stability of the local oscillator is to use a reference clock which is more stable than the Vectron.

I contacted Achim Vollhardt DH2VA asking him if it was possible to record the downlink of the BPSK beacon at Bochum, so as to have a recording referenced to the Z3801A GPSDO in Bochum, which is much more stable than the Vectron. He and Mario Lorenz DL5MLO have been very kind and they have taken the effort to make a recording for me. This post is an analysis of this recording made at Bochum.

More frequency measurements of the QO-100 NB transponder

This post is a follow up to my experiments about measuring the stability of the QO-100 NB transponder local oscillator. I am now using the Vectron MD-011 GPSDO that Carlos Cabezas EB4FBZ has lent me to reference all my QO-100 groundstation (see more information about the Vectron GPSDO in this post).

The Vectron MD-011 has an Allan deviation of \(10^{-11}\) at \(\tau = 1\,\mathrm{s}\) and \(2\cdot10^{-11}\) at \(\tau = 10\,\mathrm{s}\) according to the datasheet, so it is an improvement of an order of magnitude compared to my DF9NP TCXO-based GPSDO. I have made more measurements with the Vectron MD-011 as in my previous experiments, measuring the phase of the BPSK beacon transmitted from Bochum and a CW tone transmitted with my station. This post summarizes my results and conclusions.

Can my station measure the QO-100 NB transponder LO stability?

Following a long discussion with Bernd Zoelgert DL2BZ about the frequency stability of the local oscillator of the QO-100 narrowband transponder, I have decided to try to measure the Allan deviation of the transponder. The focus here is on short-term stability, so we are concerned with observation intervals around \(\tau = 1 \mathrm{s}\).

Of course, as with any measurement problem, the performance of the measurement equipment should be better than the “device under test”. In this case, to measure the QO-100 LO it is necessary to compare it against a reference clock which is more stable (ideally an order of magnitude better).

My whole station is locked to a DF9NP GPSDO, which is a 10MHz VCTCXO disciplined by a uBlox LEA-4S GPS receiver. That’s great to measure long-term stability, but for short-term measurements you are essentially relying on the stability of the VCTCXO, which is not so great. Therefore, the whole purpose of this experiment is first to determine whether my station is actually able to measure the QO-100 LO or not. Spoiler: it turns out the answer is “no”, as in most articles whose title is phrased as a question.

Sun observations at 10GHz

Around October 9 it was the sun outage season for Es’hail 2 as seen from Madrid. This means that the sun passed behind Es’hail 2, so it was the perfect occasion to observe the sun with my QO-100 groundstation, which has a 1.2m offset dish antenna pointing to Es’hail 2. This is an account of the measurements I made, and their use to evaluate the receiver performance.