The experiments about measuring the frequency stability of the local oscillator of the QO-100 NB transponder with a Vectron MD-011 GPSDO I made a few days ago indicated that the Allan deviation of the local oscillator was probably better than \(10^{-11}\) for \(\tau\) between 1 and 100 seconds. The next step in trying to characterize the stability of the local oscillator is to use a reference clock which is more stable than the Vectron.
I contacted Achim Vollhardt DH2VA asking him if it was possible to record the downlink of the BPSK beacon at Bochum, so as to have a recording referenced to the Z3801A GPSDO in Bochum, which is much more stable than the Vectron. He and Mario Lorenz DL5MLO have been very kind and they have taken the effort to make a recording for me. This post is an analysis of this recording made at Bochum.
The equipment used at Bochum is as follows. A HP Z3801A GPSDO is used as a 10MHz reference. An Octagon LNB is used for downlink reception with a 27MHz reference generated by a DF9NP PLL connected to the GPSDO. The IF from the LNB comes into an AMSAT-DL downconverter, also referenced to the 10MHz GPSDO, and the output of that comes into an Airspy.
The external clock input of the Airspy is connected to the 10MHz GPSDO, but Mario is not sure if this is enabled properly, as he can’t find an option in the software (it might be enabled automatically by the hardware). I couldn’t find anything helpful on the internet either. In any case, after seeing the results of the test, it seems that either the Airspy was indeed locked to the GPSDO or that at the IF it is running its stability doesn’t spoil the Allan deviation.
The recording was made on 2019-11-24 22:45:50 UTC and lasted for 956 seconds. The format was IQ at 39062sps, with the BPSK beacon centred near 0Hz.
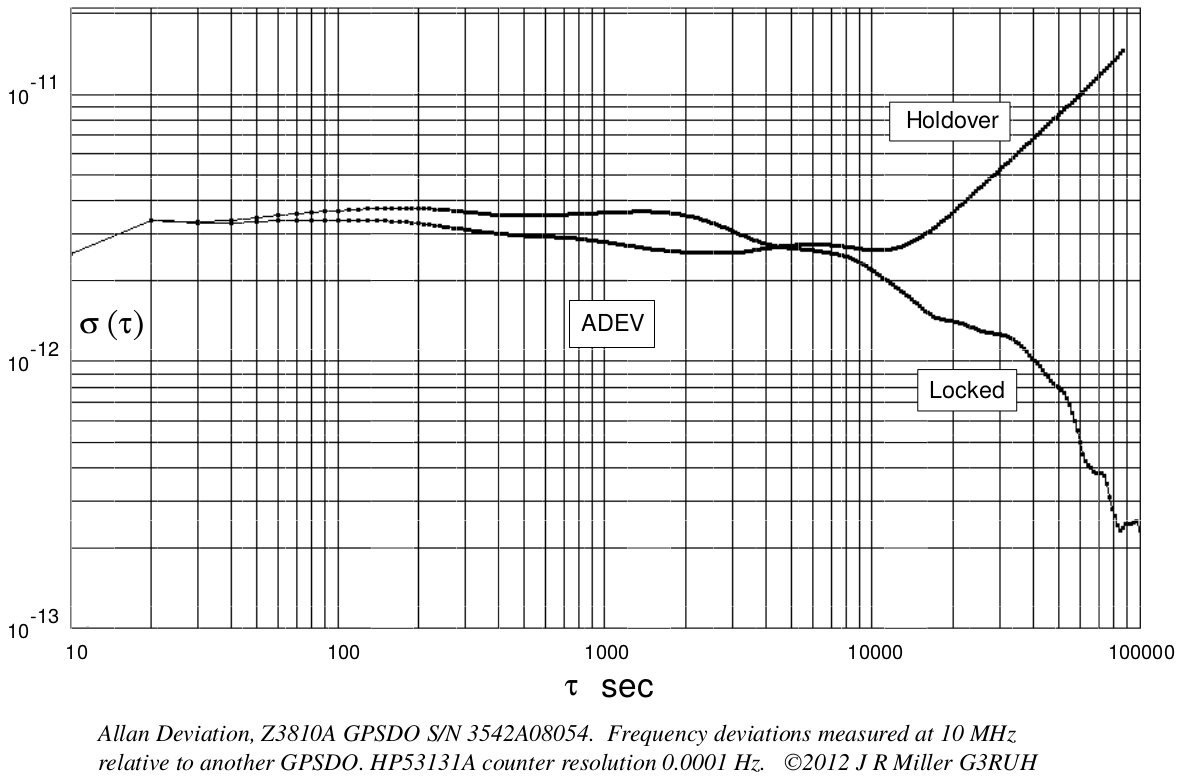
The Z3801A GPSDO used at Bochum was provided by James Miller G3RUH. He has sent me the figure shown below, which depicts the Allan deviation of the unit that is running in Bochum. We see that the deviation is around \(3\cdot 10^{-12}\) or \(4\cdot 10^{-12}\) for the range of \(\tau\)’s we are measuring in these experiments.
The recording has been processed with the GNU Radio companion flowgraph test_bochum.grc to obtain phase measurements. As usual, a Costas loop with a bandwidth of 10Hz is used to recover the suppressed carrier, and phase measurements at a rate of 100Hz are stored in a file. This file is then analysed with this Jupyter notebook.
Since in this experiment the transmitter and receiver of the BPSK beacon are both locked to the same clock, the interpretation of the results is simple: as explained in this post, it can be understood as a clock comparison between the Bochum GPSDO and the QO-100 NB transponder local oscillator at a frequency of 8089.5MHz.
The phase difference between the QO-100 local oscillator and the clock at Bochum after removing a linear trend due to frequency offset is shown in the figure below. The quadratic trend is caused by the movement of the satellite. The effects of Doppler in these kind of measurements were treated in my previous post.

Since the observation is short (slightly less than 1000 seconds), we can assume that the frequency drift due to Doppler is constant. Therefore, we can remove the Doppler by fitting a degree two polynomial to the phase difference shown above. The results are shown in the figure below. The frequency drift due to Doppler is \(4.5\cdot 10^{-14}\, 1/\mathrm{s}\). According to the theoretical study I did in the previous post, this is a typical value for the Doppler change rate. An improved measurement could be done at the moments when the Doppler change rate is zero, which happens twice a day.
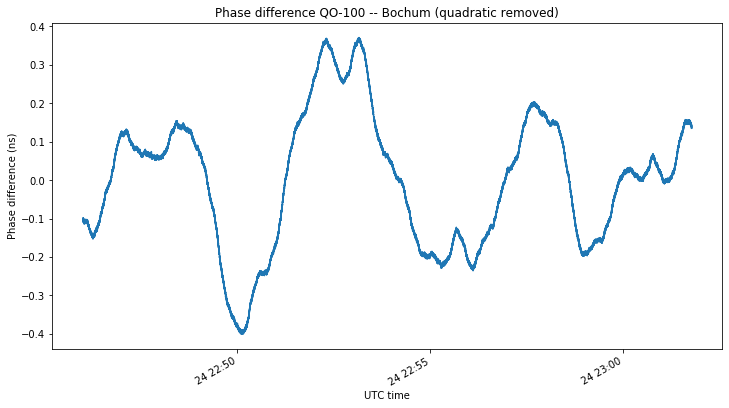
The phase differece only drifts to +/-0.4ns, which is much better than the results obtained with the Vectron MD-011 GPSDO, so we already see that the Z3801A is much more stable.
The Allan deviation both for the measurements without removing the quadratic term (blue) and with the quadratic term removed (orange) are shown below. We see that for \(\tau\) between 1 and 10 seconds the Allan deviation is between \(2\cdot 10^{-12}\) and \(3\cdot 10^{-12}\).
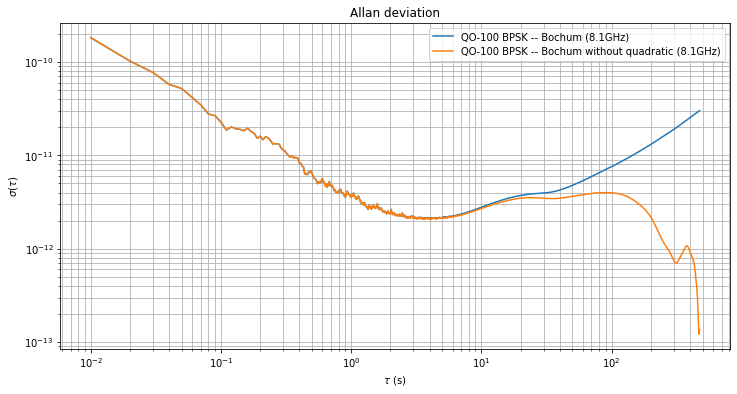
For the blue trace, the frequency drift due to Doppler starts playing a significant role for \(\tau > 30\,\mathrm{s}\). Indeed, a constant drift of \(a\) in units of 1/s contributes to the Allan deviation as \(a \tau / \sqrt{2}\). Here we have \(a = 4.5\cdot 10^{-14}\, 1/\mathrm{s}\), and we are concerned with stability on the order of \(10^{-12}\), so the Doppler drift starts playing a role for \(\tau\) on the order of 10 seconds.
In the orange trace we see some indication about what the deviation would look like if Doppler was not present. I wouldn’t trust the values for \(\tau > 200\,\mathrm{s}\), where the deviation falls very steeply, as it is likely they are too unrealistic due to the procedure used to remove the Doppler.
My interpretation of the results of these measurements is that the QO-100 local oscillator is at least as stable as the Z3801A, for \(\tau\) between 1 and 100 seconds, and possibly somewhat more stable. The Allan deviation we have measured matches the characterization of the Z3801A done by James rather well. Note that James’ plot only goes down to 10 seconds, where the deviation is around \(2.5 \cdot 10^{-12}\), and we got a deviation of \(2\cdot 10^{-12}\) at 10 seconds.
This means that the QO-100 local oscillator has a very good short-term stability. I think it would be hard to find an Amateur station having better stability, and in fact in my quest to measure the QO-100 LO Allan deviation I haven’t found any one yet. Achim points out that a good clock to measure the QO-100 LO would be the Oscilloquartz BV8607, which is below \(10^{-13}\). However these are rather hard and/or expensive to come by.
Many thanks to Achim, Mario, the rest of the AMSAT-DL team, and to James for their collaboration in this series of experiments.
One comment