A few weeks ago I posted how I make wideband recordings of bandscope data with my Hermes-Lite 2. In that post, I sort of promised to do a small analysis of the waterfall I showed. After being busy with other things (PicSat’s launch among them), I’ve finally had time to write something up.
Category: Amateur radio
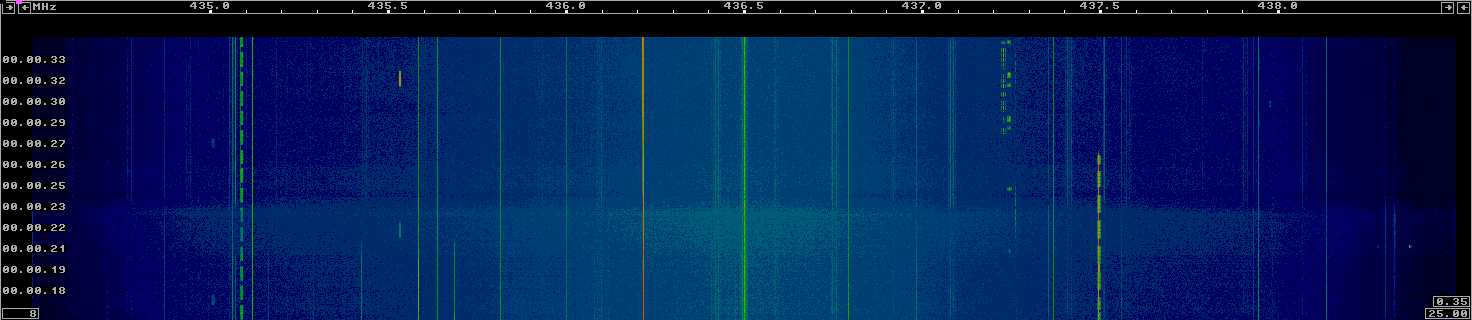
A first look at TY-2
TY-2 is a 6U Chinese cubesat that was launched on January 19th in a CZ-11 rocket from Jiuquan, together with several other small satellites, including TY-6. According to the IARU Satcoord, TY-2 and TY-6 transmit 9k6 GMSK telemetry in the 70cm Amateur satellite band (435.350MHz for TY-2 and 436.100MHz for TY-6).
Several Amateurs such as K4KDR and PD0OXW have tried to decode the packets from TY-2 and TY-6 without success. I have taken a look to an IQ recording of TY-2 that Scott K4KDR has sent me and at least I’ve managed to do something (though not much) with it. Here I describe my findings.
PicSat telemetry parser added to gr-satellites
PicSat is a recently launched cubesat from the Observatoire de Paris. It is designed to observe the Beta Pictoris star system, using a telescope based on an optical fibre. It transmits telemetry in the 70cm Amateur satellite band and it also carries a V/U FM Amateur transponder as a secondary payload. In my previous post, I decoded the 1k2 BPSK + G3RUH AX.25 packets from PicSat, and added a decoder to gr-satellites. Now I have added a telemetry parser to the gr-satellites decoder.
Decoding satellites from the PSLV 2018-004 launch
On Friday 12 at 03:59 UTC, a PSLV-CA launched from Satish Dawan Space Centre, India, to deliver Cartosat-2F, as well as some smaller satellites, into a Sun-synchronous polar orbit. Cartosat-2F is an Earth observation satellite for cartographic applications. The ride was shared by several Amateur satellites: FOX-1D, which is AMSAT-NA‘s third 1U FM cubesat, and the first one supporting the L/V mode (as well as the usual U/V mode); PicSat, a 3U cubesat from the Observatoire de Paris designed to observe the Beta Pictoris star system, which also carries a V/U FM transponder for Amateur use; CNUSail-1, a solar sail demonstrator 3U cubesat from Chungham National University, South Korea; CANYVAL-X 1 & 2, a system from Yonsei University, South Korea, consisting of a 1U and a 2U cubesat in formation flight which form a virtual telescope (with the light focusing unit in one cubesat and the detector in the other); KAUSAT-5, a 3U infrared Earth observation cubesat from Korea Aerospace University; and STEP Cube Lab, a 1U cubesat from Chosun University, Korea. There were also several non-Amateur small satellites in the launch.
On Saturday 13 morning, at 09:54:46 UTC, I did a recording of the 70cm Amateur satellite band to try to receive and decode all these satellites. I used a 7 element handheld yagi from Arrow and a LimeSDR directly connected to the antenna with a short coaxial cable. My location was approximately 40.5961º N, 3.6963º W, 700m ASL (locator IN80do). The recording is IQ at 4Msps, centred at 436.5MHz, and lasts 8 minutes and 4 seconds. Here I detail my analysis of the recording.
Saving and plotting bandscope data with the Hermes-Lite 2
The Hermes-Lite 2 and other SDR transceivers based on the openHPSDR protocol support sending bandscope data from the SDR to the PC. The bandscope data consists in fixed-length chunks of samples taken directly from the ADC. Since the ADC in a DDC receiver runs at a high sampling rate, by taking the Fourier transform of these chunks, the bandscope data can be used to display a spectrum or waterfall of a huge frequency range, covering all the HF bands. In the case of the Hermes-Lite 2, the ADC samples at 76.8MHz, so the bandscope data gives us a spectrum from 0 to 38.4MHz.
Note that the the chunks of the bandscope data are not contiguous. Streaming samples at 76.8MHz from the ADC into the PC continuously would be a lot of data. Thus, a chunk is taken and stored in the FPGA and then sent to the PC slowly. Therefore, bandscope data is only intended for wideband spectral analysis and probably has very little use outside of that.
By recording and processing the bandscope data, one can produce plots similar to the full day waterfall from the University of Twente WebSDR. Here I describe my first tests using Python.
Interfacing the Hardrock-50 HF amplifier to the Hermes-Lite 2
Since several months ago, I’m operating my HF station “remotely” from another room in the house. The station consists of a Hermes-Lite 2.0 beta2, a Hardrock-50 HF amplifier, and an outdoor MFJ-993BRT antenna tuner. My plan is to operate all of this from a laptop with ethernet connection from anywhere in the house.
The Hermes-Lite poses no problem, since it is always controlled by ethernet only. However, I need to be able to operate the Hardrock amplifier remotely: I need to change the bands, which is usually done via buttons on its front panel, and to check the output power and SWR, if only to be sure that the antenna tuner has found a tuning solution. This is usually done by looking at the Hardrock front panel display or by looking at a Diamond SX20C power/SWR meter that I also have installed in the shack.
I have taken advantage of the holidays to finish making all of this controllable by ethernet. Here I describe my solution.
A CODAR advent
Over the last few days, I have been recording CODAR on 4463kHz to produce images of the ionosphere. I started on Friday 15th and the plan was to leave the recording running until Christmas Day, thus producing some kind of “CODAR advent” images. Unfortunately, there seems to be a problem when the receiver runs for several days that results in the sudden loss of the CODAR signal. This problem can be seen at the bottom of the image below. Thus, I have finished the recording on the morning of the 24th. The equipment and software used is the same that I detailed in a previous post.
Respuesta al artículo “¿Por qué asociarse?” por EA1URA
English summary: This is an opinion post discussing the reasons given by EA1URA to join URE, the National Amateur Radio Spanish society. My main point is that the services offered by the society do not justify the fees and that the society doesn’t properly represent the interests of Amateurs with a profile similar to mine.
Normalmente no escribo artículos de opinión ni tampoco escribo en español en este blog, pero en este caso he creído conveniente hacer una excepción. Recientemente, EA1URA (URE Asturias) publicaba un artículo titulado “¿Por qué asociarse?” en el que da una lista de razones por las que merece la pena asociarse a URE. Ayer, en Twitter, @ea1ura me pasaba directamente el enlace del artículo. Tras una breve lectura, yo contestaba que ninguno de los puntos que exponen me parecen económicamente interesantes para un Radioaficionado de mi perfil y que no consideraba que URE defendiera adecuadamente mis intereses.
En este post intento extender y justificar mi respuesta, con la esperanza de que quizás sirva como crítica constructiva. Durante el artículo incluiré algunas comparaciones con la situación en Reino Unido: la RSGB y su normativa. Esto es simplemente porque es el único país extranjero donde conozco bien la situación, al haber residido allí. En general, considero que la situación en Reino Unido está bastante mejor que en España y deberíamos intentar copiar algunas cosas de allí. Imagino que cualquiera que tenga un buen conocimiento de la situación en otros países europeos como Alemania u Holanda puede tener una impresión similar.
Using CODAR for ionospheric sounding
CODAR is an HF radar used to measure surface ocean currents in coastal areas. Usually, it consists of a chirp which repeats every second. The chirp rate is usually on the order of 10kHz/s, and the signal is gated in small pulses so that the CODAR receiver can listen between pulses. The gating frequency can be on the order of 1kHz.
CODAR can be received by skywave many kilometers inland. Being a chirped signal, it is easy to extract the multipath information from the received signal. In this way, one can see the signal bouncing off the different layers of the ionosphere, and magnificent pictures showing the changes in the ionosphere (especially at dawn and dusk) can be obtained. For instance, see these images by Pieter Ibelings N4IP, or the image at the top of this post, which contains 48 hours worth of CODAR data.
Here I describe my approach to receiving CODAR. It uses GNU Radio for most of the signal processing, and Python with NumPy, SciPy and Matplotlib for plotting.
A brief study of TLE variation
During my research and experiments about using WSJT-X modes through linear transponder satellites, one of the questions I had is by how much do TLEs of different epochs for the same satellite vary. This was glimpsed in part II, where I plotted the “best delay” parameter for TLEs of different age.
The topic of accuracy in TLE computation and propagation is rather complex. A NORAD TLE is the result of an orbit determination after several radar measurements at different epochs, so the elements are in some sense “averaged” over time. Also, the SGP4 propagator is simple and doesn’t model many orbit perturbations. However, NORAD TLEs are specially crafted to give improved results when used with SGP4.
Nevertheless, here I present a simple way of studying the rate of change of NORAD TLEs at different epochs. This procedure might not be very meaningful or sophisticate, but still seems to yield some interesting results.