In a previous post I spoke about the images of the Moon and Earth taken by the Chinese lunar-orbiting satellite DSLWP-B between October 6 and 10. Some images taken during these days hadn’t been downloaded yet. The activities have continued during this week by downloading the remaining images and taking and downloading new images. This is a report of the images downloaded between October 14 and 19.
Category: Space
Spacecraft and space science
DSLWP-B Moonbounce cross-correlation analysis
In one of my latest posts I commented on the Moonbounce signal of the Chinese lunar satellite DSLWP-B, as received in Dwingeloo. In the observation made in 2018-10-07 Cees Bassa discovered a signal in the waterfall of the Dwingeloo recordings that seemed to be a reflection off the Moon of DSLWP-B’s 70cm signal. My analysis showed that the Doppler of this signal was compatible with a specular reflection on the lunar surface.
In this post I study the cross-correlation of the Moonbounce signal against the direct signal. This gives some information about how the radio signals behave when reflecting off the Moon. Essentially, we compute the Doppler spread and time delay of the Moonbounce channel.
Report of the DSLWP-B Amateur observations of the Moon and Earth
The Chinese microsatellite DSLWP-B has been in lunar orbit since 25 May 2018. This satellite carries an Amateur radio payload which includes a small 640×480 CCD camera. The JPEG images taken by the camera can be transmitted using the SSDV protocol at 125 bits per second in the 70cm Amateur satellite band.
Update 17:00 UTC: Wei comments that the camera sensor is CMOS, not CCD, and it has 2592×1944 pixels. The image is resampled to 640×480 to save memory and bandwidth.
The orientation of the camera is fixed: the camera is mounted looking in the opposite direction of the solar panel, which is usually kept pointing directly to the Sun. Therefore, the camera is usually looking directly away from the Sun. The possibility of imaging celestial bodies such as the Moon and the Earth depends on the relative positions of these and the Sun.
During the first week of October there was a new Moon, which implied that it was possible to take images of the Moon and the Earth, as I have described in this post and this other post. This is a report of all the images taken and downloaded during the observation window.
DSLWP-B Moonbounce
If you have been following my latest posts, you will know that a series of observations with the DSLWP-B Inory eye camera have been scheduled over the last few days to try to take and download images of the Moon and Earth (see my last post). In a future post I will do a chronicle of these observations.
On October 6 an image of the Moon was taken to calibrate the exposure of the camera. This image was downlinked on the UTC morning of October 7. The download was commanded by Reinhard Kuehn DK5LA and received by the Dwingeloo radiotelescope.
Cees Bassa observed that in the waterfalls of the recordings made in Dwingeloo a weak Doppler-shifted signal of the DSLWP-B GMSK signal could be seen. This signal was a reflection off the Moon.
As far as I know, this is the first reported case of satellite-Moon-Earth (or SME) propagation, at least in Amateur radio. Here I do a Doppler analysis confirming that the signal is indeed reflected on the Moon surface and do some general remarks about the possibility of receiving the SME signal from DSLWP-B. Further analysis will be done in future posts.
DSLWP-B upcoming observations of Moon and Earth
Yesterday I looked at the photo planning for DSLWP-B, studying the appropriate times to take images with the DSLWP-B Inory eye camera so that there is a chance of getting images of the Moon or Earth. As I remarked, the Earth will be in view of the camera over the next few days, so this is a good time to plan and take images.
I asked Wei Mingchuan BG2BHC to compare his calculations with mine and shortly after this he emailed me his planning for observations between October 8 and 10. After measuring the field of view of the camera as 37×28 degrees, we can plot the angular distances between the Moon or Earth and the centre of the camera to check if the celestial body will be in the field of view of the camera.
The image below shows the angular distance between these celestial bodies and the centre of the camera. As we did in the photo planning post, we assume that the camera points precisely away from the Sun. Since the Moon and Earth (especially the Moon) have an angular size of several degrees, we plot the centre of these objects with a dashed line and the edges which are nearest and furthest from the camera centre with a solid line.
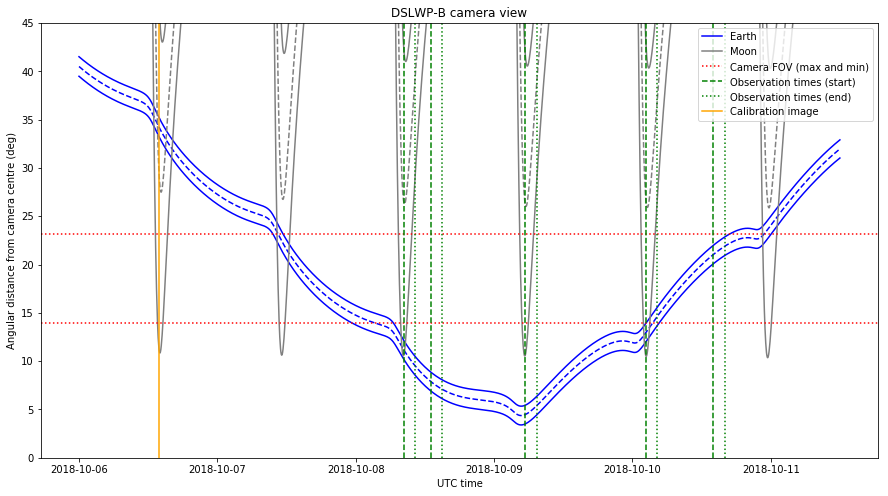
The field of view of the camera is represented with dotted red lines. Since the field of view is a rectangle, we have one mark for the minimum field of view, which is attained between the centre of the image and the centre of the top or bottom edge, and another mark for the maximum field of view, which is attained between the centre of the image and each of the corners.
The rotation of the spacecraft around the camera axis is not controlled precisely, so objects between the two red lines may or may not appear in the image depending on the rotation. Objects below the lower red line are guaranteed to appear if the pointing of the camera is correct and objects above the upper red line will not appear in the image, regardless of the rotation around the camera axis.
To calibrate the exposure of the camera, an image was taken yesterday on 2018-10-06 13:55 UTC. This time is marked in the figure above with an orange line. The image was downloaded this UTC morning. The download was commanded by Reinhard Kuehn DK5LA and received by Cees Bassa and the rest of the PI9CAM team in Dwingeloo. This image is shown below.

The image shows an over exposed Moon. Here we are interested in using the image to confirm the orientation of the camera. The distance between the centre of the image and the edge of the Moon is 240 pixels, which amounts to 14 degrees. The plot above gives a distance of 11 degrees between the edge of the Moon and the camera centre.
Thus, it seems that the camera is pointed off-axis by 3 degrees. This error is not important for scheduling camera photos, since an offset of a few degrees represents a small fraction of the total field of view and the largest error in predicting what will appear in the image is due to rotation of the spacecraft around the camera axis.
The observations planned by Wei for the upcoming days are shown in the plot above by green lines. The start of the observation is marked with a dashed line and the end of the observation (which is 2 hours later) is marked with a dotted line. The camera should take an image at the beginning of the observation and then we have 2 hours to download the image during the rest of the observation.
We see that Wei has taken care to schedule observations exactly on the next three times that the Moon will be closest to the camera centre. This gives the best chance of getting good images of the lunar surface (but the Moon will only fill the image partially, as in the picture shown above).
There are also two additional observations planned when the Moon is not in view. The first, on October 8 is guaranteed to give a good image of the Earth. The second, on October 10 will only give an image of the Earth if the rotation of the spacecraft is right.
The orbital calculations for the plot shown above have been done in GMAT. I have modified the photo_planning.script script to output a report with the coordinates of the Earth and the Moon in the Sun-pointing frame of reference (see the photo planning post).
The angle between the centre of the camera and the centre of the Earth of the Moon can be calculated as\[\arccos\left(\frac{x}{\sqrt{x^2+y^2+z^2}}\right),\]where \((x,y,z)\) are the coordinates of the celestial body in the Sun-pointing frame of reference. The apparent angular radius of the celestial body can be computed as\[\arcsin\left(\frac{r}{\sqrt{x^2+y^2+z^2}}\right),\]where \(r\) is the mean radius of the body.
These calculations and the plot have been made in this Jupyter notebook.
DSLWP-B camera field of view
In my previous post, I wondered about what was the field of view of the Inory eye camera in DSLWP-B. Wei Mingchuan BG2BHC has answered me on Twitter that the field of view of the camera is 14×18.5 degrees. However, he wasn’t clear about whether these figures are measured from the centre of the image to one side or between two opposite sides of the image. I guess that these values are measured from the centre to one side, since otherwise the total field of view of the camera seems too small.
Here I measure the field of view of the camera using the image of Mars and Capricornus taken on August 4, confirming that these numbers are measured from the centre of the image to one side, so the total field of view is 28×37 degrees.
DSLWP-B photo planning
As you may already know, most of the pictures taken so far by the DSLWP-B Inory eye camera have been over-exposed purple things. In order to take more interesting pictures, such as pictures of the Earth and the Moon, we have to plan ahead and know when these objects will be in view of the camera.
The picture below shows a diagram of DSLWP-B. The solar panel is behind the main body, pointing towards the back right. The Inory eye camera points in the opposite direction, towards the front left of the diagram. The camera is located in the front panel of the Amateur radio module, which is one of the pink modules.
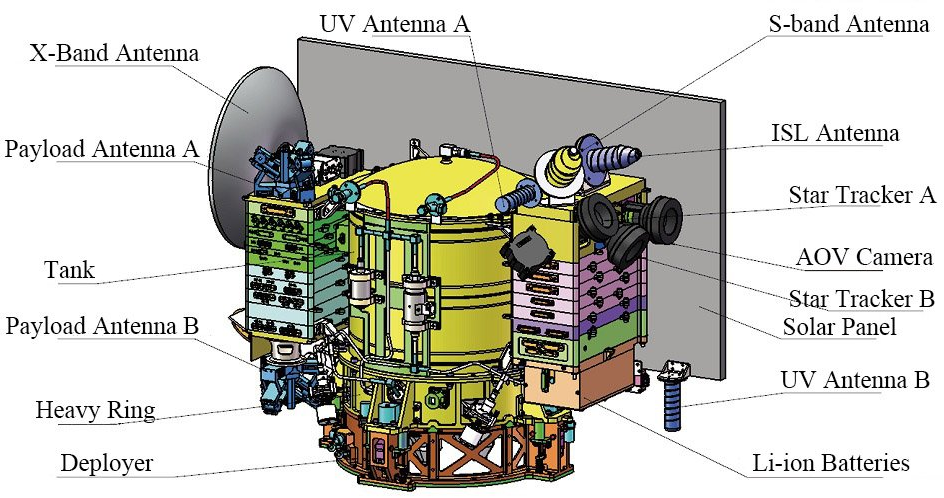
In the nominal flight configuration, the solar panel is pointed towards the Sun to gather the maximum amount of sunlight. Therefore, the camera should point opposite to the Sun. This is good, because objects in the field of view of the camera are guaranteed to be well illuminated and it also prevents the Sun from appearing in the image, causing lens flare.
In one of the images taken previously by the camera there is a very bright lens flare, possibly caused by the Sun hitting the camera directly. This seems to indicate that the spacecraft is not always in the nominal flight orientation. As the orientation is very important when doing photo planning, here we assume that the spacecraft is always oriented in the nominal flight configuration, with its camera pointing opposite to the Sun.
We use GMAT with the 20181006 tracking file from dswlp_dev for the orbital calculations. The GMAT script can be downloaded here.
To simulate the orientation of the camera in GMAT, I have used an ObjectReferenced coordinate system. The primary is the Sun, the secondary is DSLWP-B, and the axes are chosen as X = R, Z = N. Therefore, the X axis points away from the Sun, in the direction of the camera. The orbit view is centred on DSLWP-B and points towards +X, so it shows what the camera would see (except for the field of view, which is not simulated).
When propagating the orbit in GMAT we see that the Earth passes near the +X axis every Lunar month and that the Moon crosses the image every orbit.
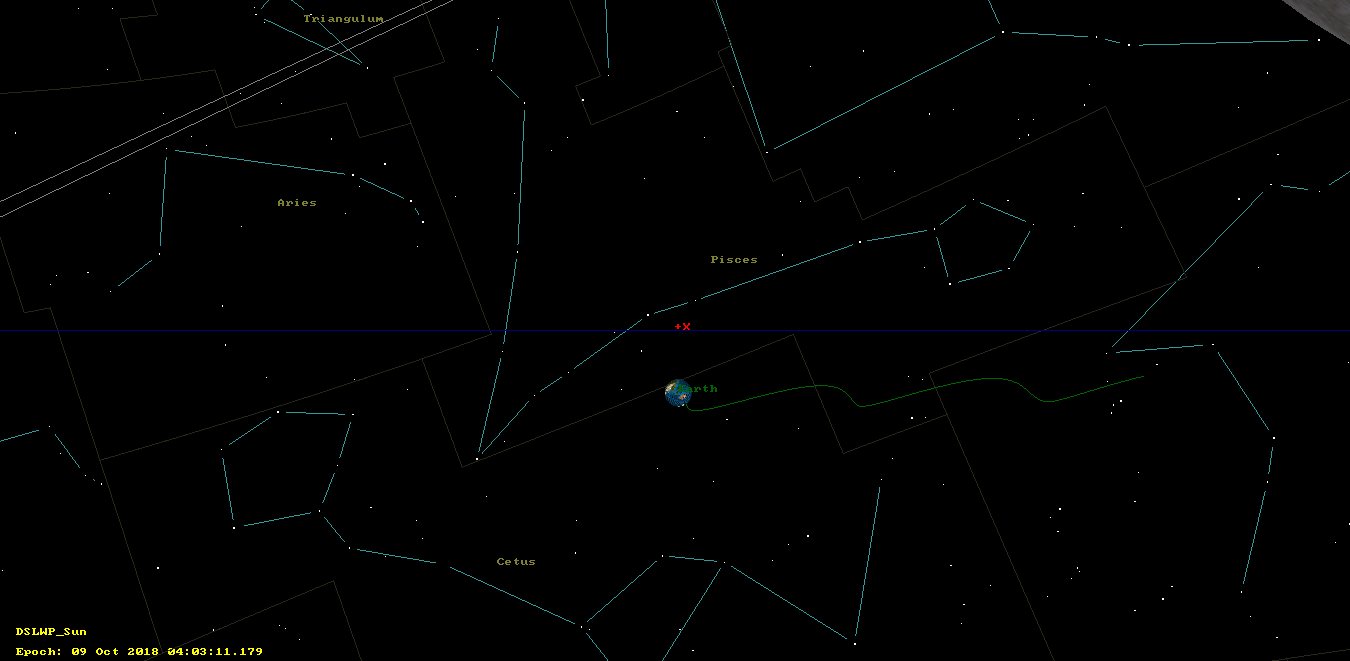
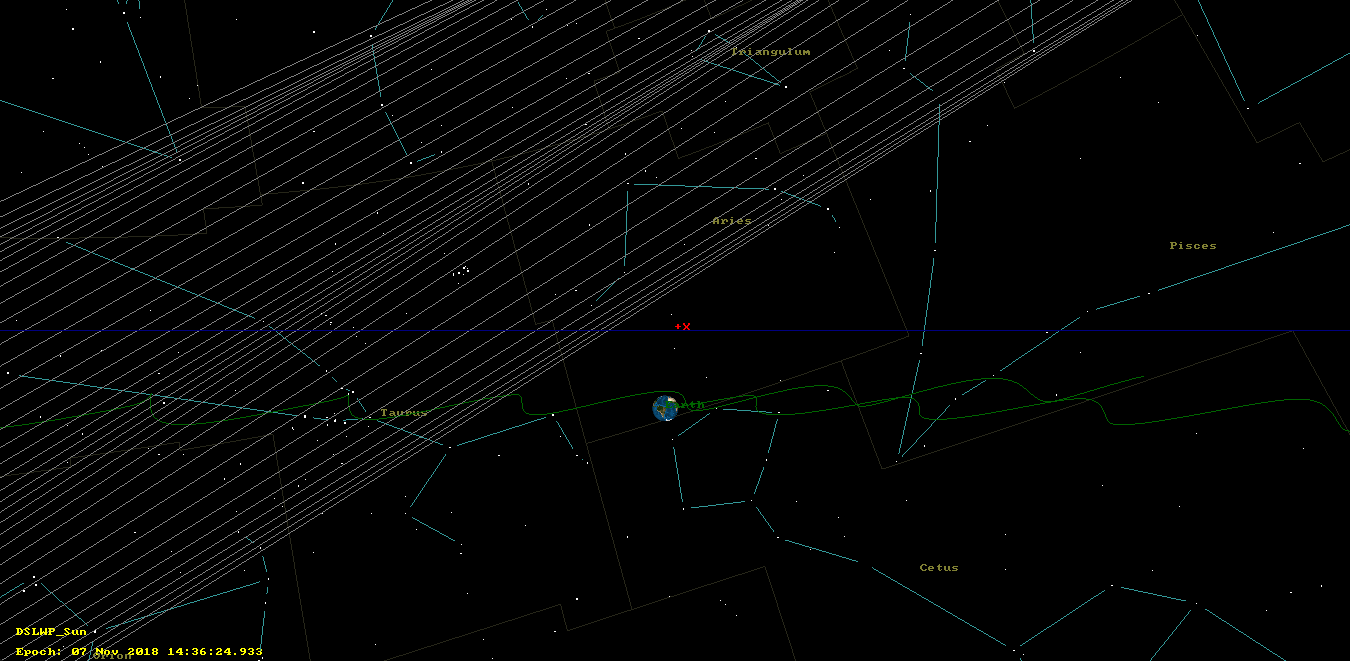
The two images below show the dates when the Earth will pass nearby the +X axis. These dates are good candidates for taking images of the Earth. From the point of view of the camera, the Earth seems to orbit slowly from right to left in these images. Therefore, there should be a tolerance of a couple of days as to when the images of the Earth could be taken.
Thus, we see that the next good dates for attempting to take images of the Earth are October 9 and November 7 (plus/minus a couple days of margin).
The Moon is much larger from the point of view of DSLWP-B and we have seen already that it fills the field of view of the camera completely. Thus, even though in this GMAT simulation the Moon crosses the screen every orbit, we need to wait until the path taken by the Moon is near the centre of the screen.
In the image below we see a good moment to take an image of the Moon. From the point of view of the camera, the Moon crosses from top to bottom of the screen every orbit and its path moves slightly to the right every time, taking it closer to the centre as we progress towards December.
Therefore, a good moment to attempt to take an image of the Moon is late October and all of November. However, the time when the picture is taken is critical, because the Moon crosses the screen quickly. It is near the +X axis only for one or two hours. Therefore, starting in late October, there will be a window of a couple hours each orbit (or each day, since the orbital period is close to one day) where photos of the Moon can be attempted.

Judging by one of Wei Mingchuan BG2BHC’s lasts tweets, he has also been thinking about dates to take good images with the camera. It would be interesting to know if his findings match what I have exposed here.
A good question when doing this sort of planning is what is the field of view of the camera. Probably this can be estimated from some of the existing images.
DSLWP-B talk in IberRadio
As you may already know if you follow me on Twitter, on Saturday September 15 I was in Ávila in the IberRadio Spanish Amateur Radio fair giving a talk about DSLWP-B. The talk was well received and I had quite a full room. I recorded my talk to upload it later to YouTube as I did last year.
Since I know that many international people would be interested in this talk and the talk was in Spanish, I wanted to prepare something in English. As I would be overlaying the slides on the video (since the video quality is quite poor and it is impossible to see the projected slides), I thought of overlaying the slides also in English and adding English subtitles.
Doing the subtitles has been a nightmare. I have been working on this non-stop since Sunday morning (as my free time allows me). I intended to use YouTube’s transcript and auto-sync feature, where you provide a transcript (in the video’s original language) and presumably an AI will auto-sync this to the video’s audio. I say presumably because in my case the auto-sync was a complete failure, so I had to resync everything by hand.
Also, since I have listened to the video over and over, I have gotten a bit bored of my own voice and noted some expressions and words that I tend to use a lot. I think this is good, because now I am more conscious when talking in public and can try to avoid using these expressions so much.
In any case, here is the final result. First you have the video with English slides:
And also you have the video with Spanish slides:
Remember that you can use either Spanish or English subtitles with any of the videos. Also, I have the translation contributions enabled, so feel free to provide subtitles in your own language if you wish.
The PDF slides for the talk can be downloaded in Spanish here and in English here.
DSLWP-B clock running late
This Wednesday, a DSLWP-B test was done between 04:00 and 06:00 UTC. During this test, a few stations reported on Twitter that they were able to receive the JT4G signal correctly (they saw the tones on the waterfall) but decoding failed.
It turns out that the cause of the decoding failures is that the DSLWP-B clock is running a few seconds late. Thus, the JT4G transmission starts several seconds after the start of the UTC minute and so the decoding fails, since WSJT-X only searchs for a time offset of a few seconds.
Lunar orbit perturbations and DSLWP-B
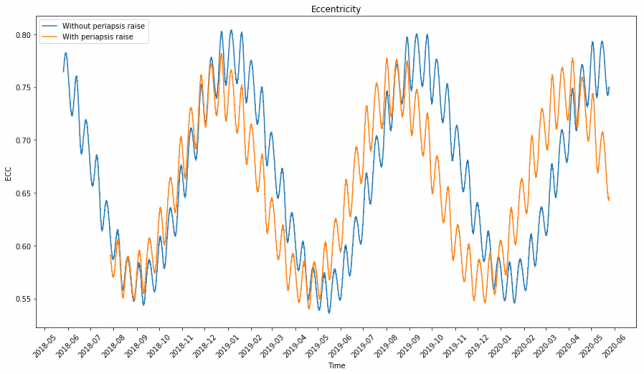
Ever since simulating DSLWP-B’s long term orbit with GMAT, I wanted to understand the cause of the periodic perturbations that occur in some Keplerian elements such as the eccentricity. As a reminder from that post, the eccentricity of DSLWP-B’s orbit shows two periodic perturbations (see the figure below). One of them has a period of half a sidereal lunar month, so it should be possible to explain this effect from the rotation of the Moon around the Earth. The other has a period on the order of 8 or 9 months, so explaining this could be more difficult.
In this post I look at how to model the perturbations of the orbit of a satellite in lunar orbit, explaining the behaviour of the long term orbit of DSLWP-B.