Yesterday I looked at the photo planning for DSLWP-B, studying the appropriate times to take images with the DSLWP-B Inory eye camera so that there is a chance of getting images of the Moon or Earth. As I remarked, the Earth will be in view of the camera over the next few days, so this is a good time to plan and take images.
I asked Wei Mingchuan BG2BHC to compare his calculations with mine and shortly after this he emailed me his planning for observations between October 8 and 10. After measuring the field of view of the camera as 37×28 degrees, we can plot the angular distances between the Moon or Earth and the centre of the camera to check if the celestial body will be in the field of view of the camera.
The image below shows the angular distance between these celestial bodies and the centre of the camera. As we did in the photo planning post, we assume that the camera points precisely away from the Sun. Since the Moon and Earth (especially the Moon) have an angular size of several degrees, we plot the centre of these objects with a dashed line and the edges which are nearest and furthest from the camera centre with a solid line.
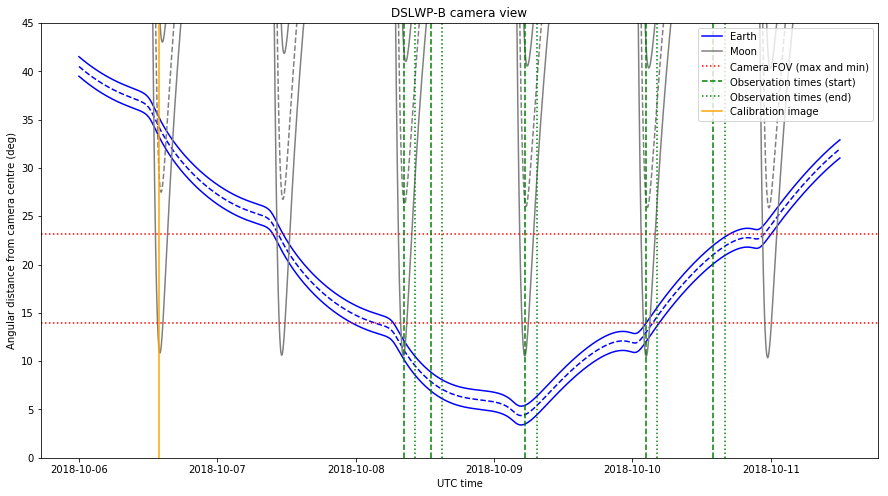
The field of view of the camera is represented with dotted red lines. Since the field of view is a rectangle, we have one mark for the minimum field of view, which is attained between the centre of the image and the centre of the top or bottom edge, and another mark for the maximum field of view, which is attained between the centre of the image and each of the corners.
The rotation of the spacecraft around the camera axis is not controlled precisely, so objects between the two red lines may or may not appear in the image depending on the rotation. Objects below the lower red line are guaranteed to appear if the pointing of the camera is correct and objects above the upper red line will not appear in the image, regardless of the rotation around the camera axis.
To calibrate the exposure of the camera, an image was taken yesterday on 2018-10-06 13:55 UTC. This time is marked in the figure above with an orange line. The image was downloaded this UTC morning. The download was commanded by Reinhard Kuehn DK5LA and received by Cees Bassa and the rest of the PI9CAM team in Dwingeloo. This image is shown below.

The image shows an over exposed Moon. Here we are interested in using the image to confirm the orientation of the camera. The distance between the centre of the image and the edge of the Moon is 240 pixels, which amounts to 14 degrees. The plot above gives a distance of 11 degrees between the edge of the Moon and the camera centre.
Thus, it seems that the camera is pointed off-axis by 3 degrees. This error is not important for scheduling camera photos, since an offset of a few degrees represents a small fraction of the total field of view and the largest error in predicting what will appear in the image is due to rotation of the spacecraft around the camera axis.
The observations planned by Wei for the upcoming days are shown in the plot above by green lines. The start of the observation is marked with a dashed line and the end of the observation (which is 2 hours later) is marked with a dotted line. The camera should take an image at the beginning of the observation and then we have 2 hours to download the image during the rest of the observation.
We see that Wei has taken care to schedule observations exactly on the next three times that the Moon will be closest to the camera centre. This gives the best chance of getting good images of the lunar surface (but the Moon will only fill the image partially, as in the picture shown above).
There are also two additional observations planned when the Moon is not in view. The first, on October 8 is guaranteed to give a good image of the Earth. The second, on October 10 will only give an image of the Earth if the rotation of the spacecraft is right.
The orbital calculations for the plot shown above have been done in GMAT. I have modified the photo_planning.script script to output a report with the coordinates of the Earth and the Moon in the Sun-pointing frame of reference (see the photo planning post).
The angle between the centre of the camera and the centre of the Earth of the Moon can be calculated as\[\arccos\left(\frac{x}{\sqrt{x^2+y^2+z^2}}\right),\]where \((x,y,z)\) are the coordinates of the celestial body in the Sun-pointing frame of reference. The apparent angular radius of the celestial body can be computed as\[\arcsin\left(\frac{r}{\sqrt{x^2+y^2+z^2}}\right),\]where \(r\) is the mean radius of the body.
These calculations and the plot have been made in this Jupyter notebook.
3 comments