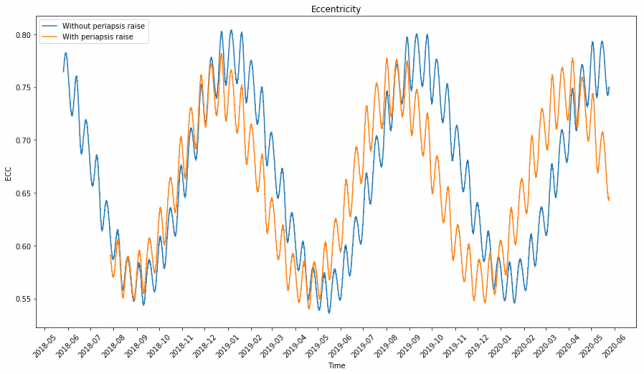
As you may already know if you follow me on Twitter, on Saturday September 15 I was in Ávila in the IberRadio Spanish Amateur Radio fair giving a talk about DSLWP-B. The talk was well received and I had quite a full room. I recorded my talk to upload it later to YouTube as I did last year.
Since I know that many international people would be interested in this talk and the talk was in Spanish, I wanted to prepare something in English. As I would be overlaying the slides on the video (since the video quality is quite poor and it is impossible to see the projected slides), I thought of overlaying the slides also in English and adding English subtitles.
Doing the subtitles has been a nightmare. I have been working on this non-stop since Sunday morning (as my free time allows me). I intended to use YouTube’s transcript and auto-sync feature, where you provide a transcript (in the video’s original language) and presumably an AI will auto-sync this to the video’s audio. I say presumably because in my case the auto-sync was a complete failure, so I had to resync everything by hand.
Also, since I have listened to the video over and over, I have gotten a bit bored of my own voice and noted some expressions and words that I tend to use a lot. I think this is good, because now I am more conscious when talking in public and can try to avoid using these expressions so much.
In any case, here is the final result. First you have the video with English slides:
And also you have the video with Spanish slides:
Remember that you can use either Spanish or English subtitles with any of the videos. Also, I have the translation contributions enabled, so feel free to provide subtitles in your own language if you wish.
The PDF slides for the talk can be downloaded in Spanish here and in English here.