In the QO-100 (Es’hail 2) narrow band transponder, the recommendation for the adjustment of your downlink signal power is not to be stronger than the beacon. This was also the recommended usage of the old AO-40. Since the transponder has two beacons marking the transponder edges: a CW beacon marking the lower edge and a 400baud BPSK beacon marking the upper edge, there has been some debate on Twitter about which beacon does this recommendation refer to and what does “stronger” mean.
Of course, more formally, signal strength means power, which is a well defined physical concept, so there should be no argument about what does power mean. However, there are two different power measurements used for RF: average power and peak envelope power. I will assume that the recommendation refers to average power, not to peak envelope power. This makes more sense from the point of view of the power budget of the satellite amplifier (The total average power it needs to deliver is just the sum of the average powers of the signals of all the users, while the behaviour of the peak envelope power is much more complicated).
Also, I think that using peak envelope power for this restriction would be a very strict requirement on high PAPR signals. Note that the PAPR of CW is 0dB and the PAPR of BPSK is between 2 and 3dB, depending on the pulse shaping, so these are rather low PAPRs. For comparison, a moderately compressed SSB voice signal has a PAPR of 6dB.
In my opinion, the main problem with these discussions about “signal strength” is that many people are trying to judge power by looking at their waterfall or spectrum display and seeing what signal looks “higher”. This kind of measurement is not any good, because it doesn’t take signal bandwidth into account, depends on the FFT size, the window function, etc. It doesn’t help that many popular SDR software don’t have a good signal meter displaying the average power of the signal tuned in the passband.
In any case, I was curious about whether the power of the two beacons is the same and whether there is any interesting change over time. I have made a GNU Radio flowgraph that measures the power of each of the two beacons and of the transponder noise, and saves them to a file for later analysis.
The measurement bandwidth is 2kHz, for each of the three signals. The transponder noise is measured 3kHz below the BPSK beacon. This frequency should usually be clean of any signals (in the transponder band plan there is a guard band of 5kHz surrounding each beacon).
The receiver is a LimeSDR and the dish is 95cm (but I’ve discovered that the dish is off focus, so the gain is comparable to a 60cm dish). Everything is frequency locked to a GPSDO. The GNU Radio flowgraph can be found here. I am also using gr-linrad to send the IQ signal to Linrad in order to listen to the stations in the transponder.
I have monitored the transponder for over 40 hours. The results are shown in the graph below. This shows the average power of the digital beacon, the CW beacon and the transponder noise (in 2kHz of bandwidth) over time. The power readings obtained from GNU Radio are averaged in windows of one minute. This is probably not what one would want to do for CW (shown in orange), since the result is affected by the duty cycle of the keying. Instead, we also take the maximum of each one minute window (shown in red), which is representative of the carrier power, ignoring keying. The vertical axis has been normalized to make the average power of the transponder noise 0dB.
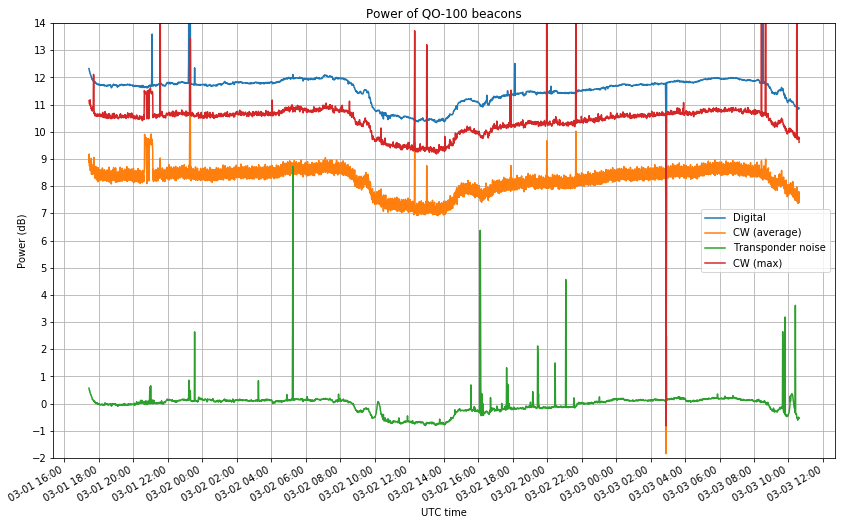
We see that the digital beacon is 1dB stronger than the CW beacon, even though in spectrum plots the CW beacon appears “higher” due to its narrower bandwidth. It is also interesting to see the variations in the power of all signals, in particular the dip between 09:00 and 15:00 UTC (which I think that happens every day).
While one should not trust the stability of the LNB gain (as it is known to change noticeably with temperature), if you look closely you will see that the transponder noise dips only 0.5dB, while the beacons dip 1.5dB, so there must be something going on at the satellite, not only at my receiver.
Another interesting measurement that can be obtained from this data is the carrier to noise density ratio (CN0) of the beacons. This is interesting, because the signals from the users are required not to exceed this CN0, so it puts an upper limit on the amount of information that a user may transmit using a digital signal through the narrowband transponder.
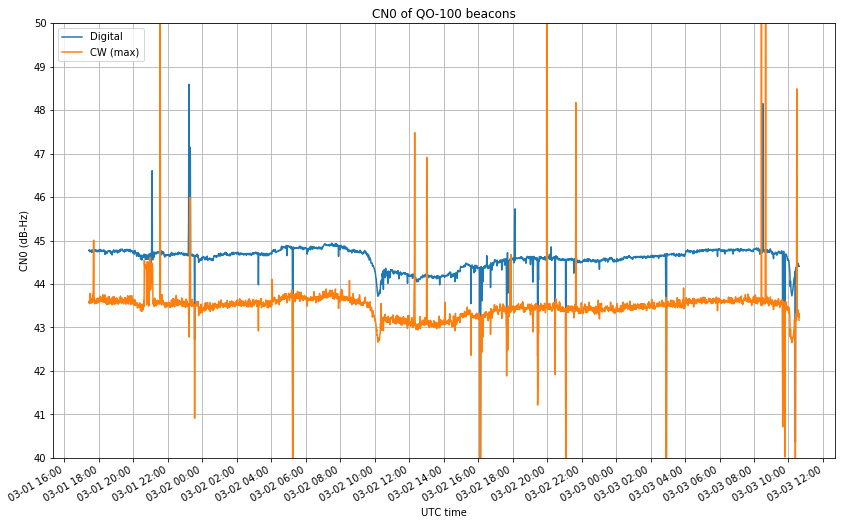
We see that the digital beacon has a CN0 of around 45dB-Hz, so we might take this value as the upper limit for user signals through the narrowband transponder. This is actually very good, allowing one to push really high bitrate signals through a typical SSB channel of 2.7kHz. Indeed, let us run some back-of-the-envelope calculations.
We aim for an Eb/N0 of 5dB. Even a simple \(r = 1/2\) Viterbi decoder has a BER smaller than \(10^{-4}\) at 5dB of Eb/N0 with BPSK or QPSK. At a CN0 of 45dB-Hz, we can push 10kbps at this Eb/N0. So we see that in an SSB channel, the more stringent requirement for pushing data is not the SNR but the bandwidth. If we think of a single carrier APSK or QAM signal at 2ksymbols/s, so as to fit nicely inside an SSB channel, with an \(r = 1/2\) FEC with need 10 bits per symbol. This is completely unreasonable, and it won’t work in practise. For comparison, the highest order DVB-S2 modulation is 32APSK, which fits 5 bits per symbol. The conclusion is clear: there is plenty of SNR to fit any reasonable digital signal we can think of in an SSB channel through the narrowband transponder.
Now, onto something more plausible, let’s say we use a 2ksps 8PSK signal, which gives a total of 6kbps. If we design for an \(r = 3/4\) FEC, we get 4.5kbps, and an Eb/N0 of 8.5dB. This should work at an acceptable BER. As a comparison, DVB-S2 with 8PSK at 3/4 needs 8dB of C/N. This would be very nice for a (rather high-fidelity) digital voice signal.
However, I am not sure that there is currently a good open source codec for digital voice at 4.5kbps. Opus only goes down to 8kbps, while Codec2 development is centred in 1.2kbps and lower. In any case, I think that the narrowband transponder of QO-100 opens up very interesting possibilities for digital voice. The AWGN channel that the satellite transponder presents is rather easy to work with (in comparison to the HF channels that the FreeDV developers try to cope with), and while SSB at 45dB-Hz of CN0 sounds good and is easy to copy, the noise is evident. Thus, I think that there is room for experimentation and that it should be possible to develop a digital voice modem that gives a more pleasant listening experience than SSB.
The graphs and calculations in this post have been done in this Jupyter notebook.
7 comments