If you’ve been following my posts about Es’hail 2, you’ll know that shortly after launch Es’hail 2 was stationed in a test slot at 24ºE. It remained in this slot until December 29, when it started to move to its operational slot at 26ºE. As of January 2, Es’hail is now stationed at 26ºE (25.8ºE, according to the TLEs).
The new GEO orbit at 26ºE is much more perfect than the orbit it had at 24ºE. This is to be expected for an operational orbit. Since December 30, I’ve been recording Doppler data of the satellite moving to its operational slot, and I have found some interesting effects of orbital dynamics in the data. This post is an account of these.
The figure below shows my Doppler measurements (corrected for transmitter frequency offset and averaged in intervals of 10 minutes). The TLE Doppler is constructed by taking the TLE whose epoch is nearest to each moment. In this way, we have large discontinuities at the point where we change from one TLE to the next one.
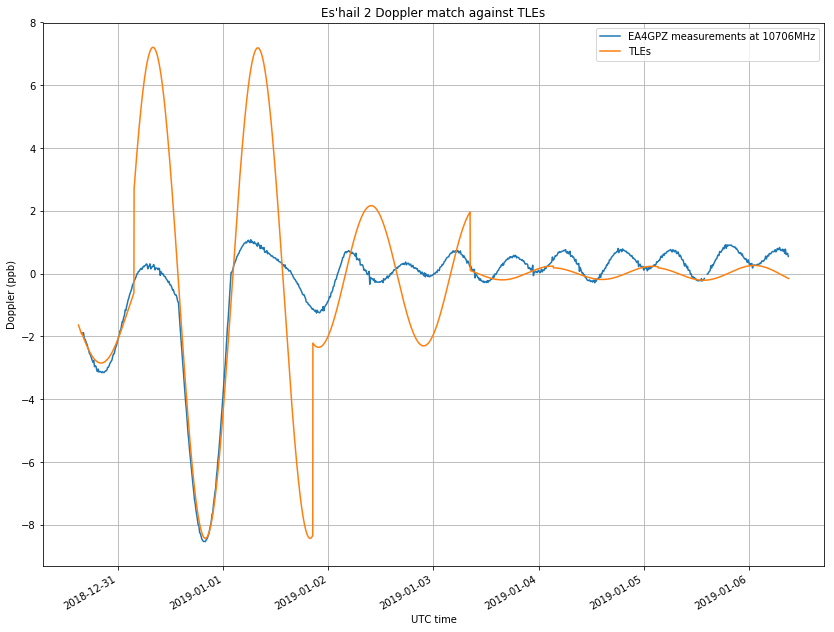
Since the spacecraft was manoeuvering during this period, the TLEs are not a very good match in general. Still, we have a rather good match during the second half of December 31. The large Doppler signal is caused by the relatively large eccentricity caused by a burn. This makes the satellite move up and down during each revolution.
The “kinks” that can be seen in the Doppler curve correspond to accelerations that happened when the rocket engines where fired. We have one on mid December 31, another just after the start of January 1, and perhaps another on the beginning of January 2.
After January 2, it seems that the spacecraft is on station and its Doppler curve shows a stable behaviour. The amplitude of the Doppler oscillations is around 0.25ppm. This is much less than the 2ppm that we found in the 24ºE test slot (see this post), indicating a more perfect GEO orbit. There is an interesting thing happening with the Doppler oscillations here: the period is half a sidereal day. In the test slot we could see oscillations whose period was one sidereal day. These were caused by a non-zero inclination or eccentricity. Any small deformation of the orbit that makes it non-GEO will manifest itself as something that has a period of one sidereal day, so at first I was left wondering about the cause of these oscillations with period equal to half a sidereal day. Also, note that the observed Doppler doesn’t match the TLE Doppler at all, and indeed the TLE Doppler is showing oscillations with a period of one sidereal day.
The answer to this will be explained later, but before, let us examine the position of Es’hail 2, as given by the TLEs, in the figure below.
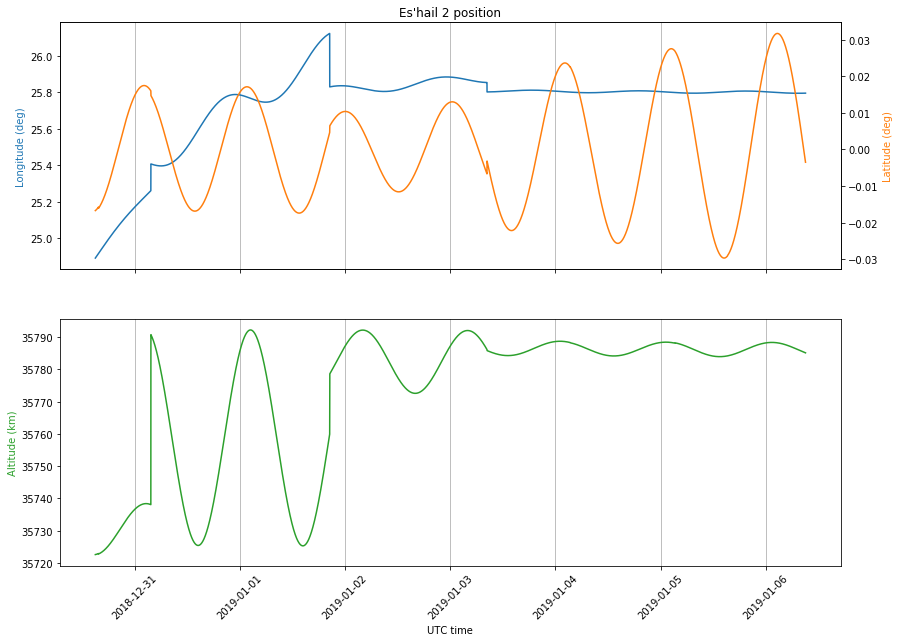
As we can see, the satellite finishes its travel to 25.8ºE and since that moment the eccentricity is close to zero, with oscillations in altitude of only a few kilometres. The inclination is also close to zero, with oscillations in a latitude of 0.03º (which corresponds to 21km). These give a very low Doppler signature.
Returning to the oscillations with period of half a sidereal day, Steen Jørgensen OZ1SEJ suggested that these may be caused by tidal forces. Actually, Steen meant solid tides, but since I knew that these have a very small (metric or sub-metric) effect, I thought of tidal effects on the satellite.
I couldn’t imagine well the effect of lunar forces on the satellite at each moment along the orbit, since most sources speak of what happens when one averages these effects over one complete revolution. Usually, this is all you care about: how the Keplerian parameters are perturbed after each revolution and how these perturbations add up over the course of many orbits to give raise to periodic and secular perturbations. However, what we care about here is how the lunar forces perturb each point of the Keplerian orbit.
To study these effects I have set up a simulation in GMAT using the following script file. This simulates one day of a satellite in a rather perfect GEO orbit near 26ºE. The force model uses only the Earth and Moon as point masses. The position of the satellite in ECEF coordinates and in a topocentric system centred on my station are stored in files for later analysis in this Jupyter notebook.
Although this is a qualitative study, the results obtained in the GMAT simulation match what I’m seeing in the Doppler measurements, so the conclusion is that these oscillations with a period of half a sidereal day are caused by the lunar forces acting on the satellite.
The figure below shows the distance between the satellite and my station. Note that this only varies around 2 or 3 kilometres.
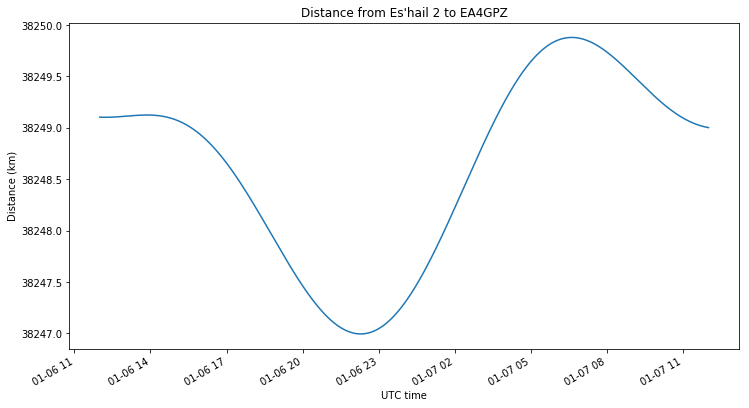
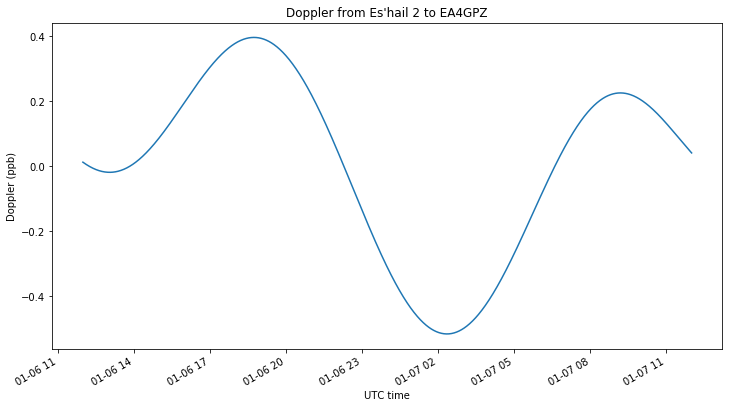
The derivative of the distance gives the Doppler curve. Note that this has a period of half a sidereal day. The amplitude of the variations is 0.4ppb, which matches more or less what we have observed in the Doppler measurements.
The figure below shows the variations in the ECEF z coordinate. These are very small, since the inclination of the orbit is set very close to zero. Note that the inclination in the MJ2000Eq coordinates used in GMAT is not zero, but near 0.1, because of precession.
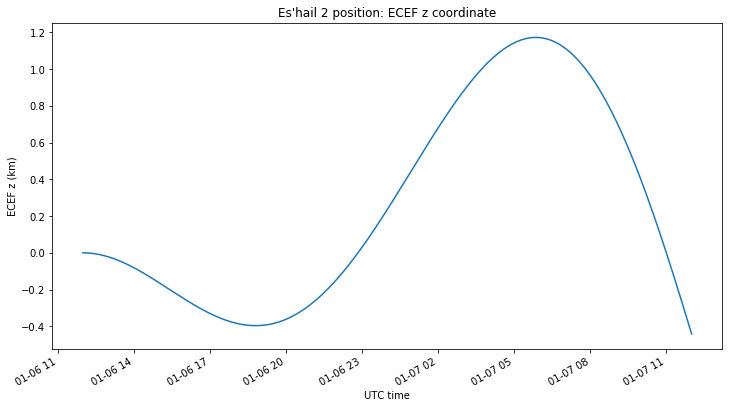
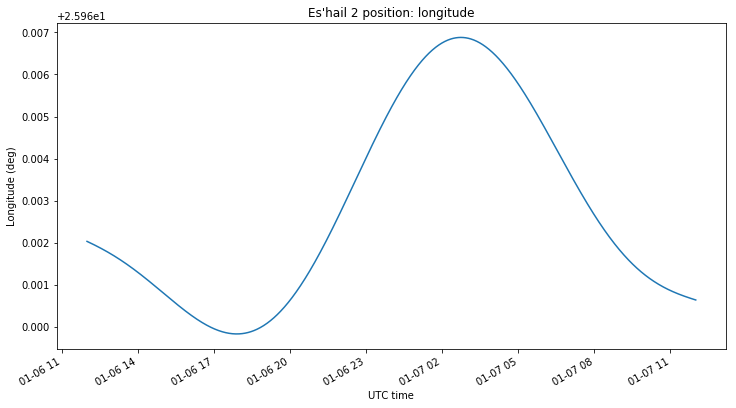
The figure below shows the longitude of Es’hail 2’s position. It only changes 0.007º over the course of the orbit, and after one revolution returns more or less to the same point, meaning that the orbital period is very close to one sidereal day.
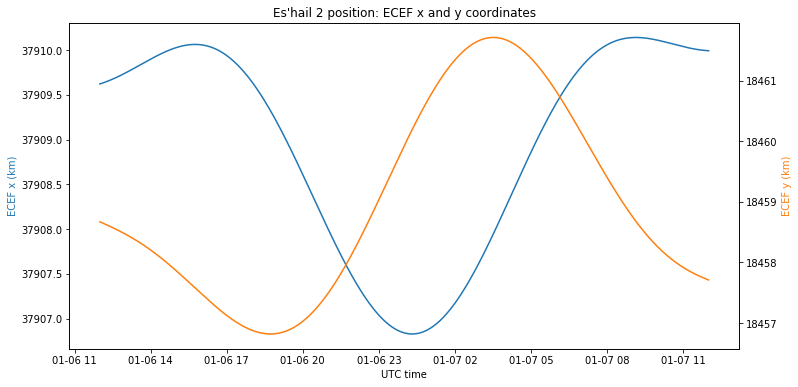
The next figure shows the variations in the ECEF x and y coordinates. These only change a few kilometres over the course of a revolution.
Finally, the next figure shows the radius of the orbit, which changes roughly 3km during the orbit. Note that this curve is very similar to the one given by the distance between the satellite and my station. As I have mentioned in this post, the movement that affects the distance to the satellite the most is the altitude changes. Therefore, the cause of the Doppler oscillations of period half a sidereal day is the change in orbital radius exerted by lunar forces.
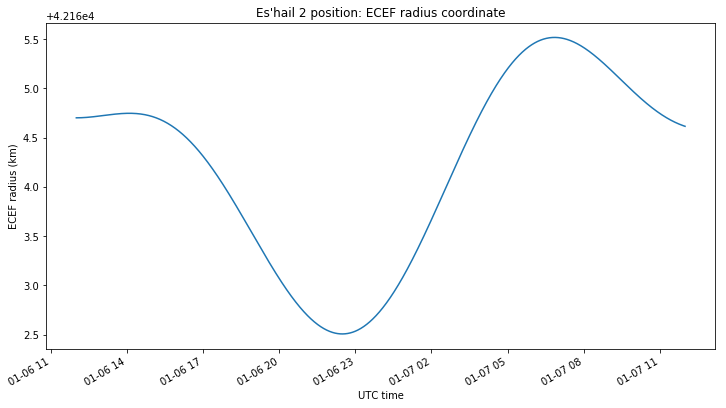
Intuitively, since the tidal forces follow the pattern given in this figure, we can divide one revolution into four quadrants and note that the effect of the tidal forces on the orbit is the same in each pair of opposite quadrants. This causes the period of half a sidereal day in the perturbations.
Also note that the perturbations caused by lunar forces are small. They cause a Doppler signal of only 0.3ppb. The larger Doppler signal caused by a non-zero inclination or eccentricity would completely swamp out this smaller signal. That is the reason why I didn’t observe any lunar perturbations when the satellite was stationed in 24ºE.
Also, it seems that these kinds of lunar perturbations are not included in the SDP4 propagator that the TLEs use, explaining their absence in the TLE Doppler curves.
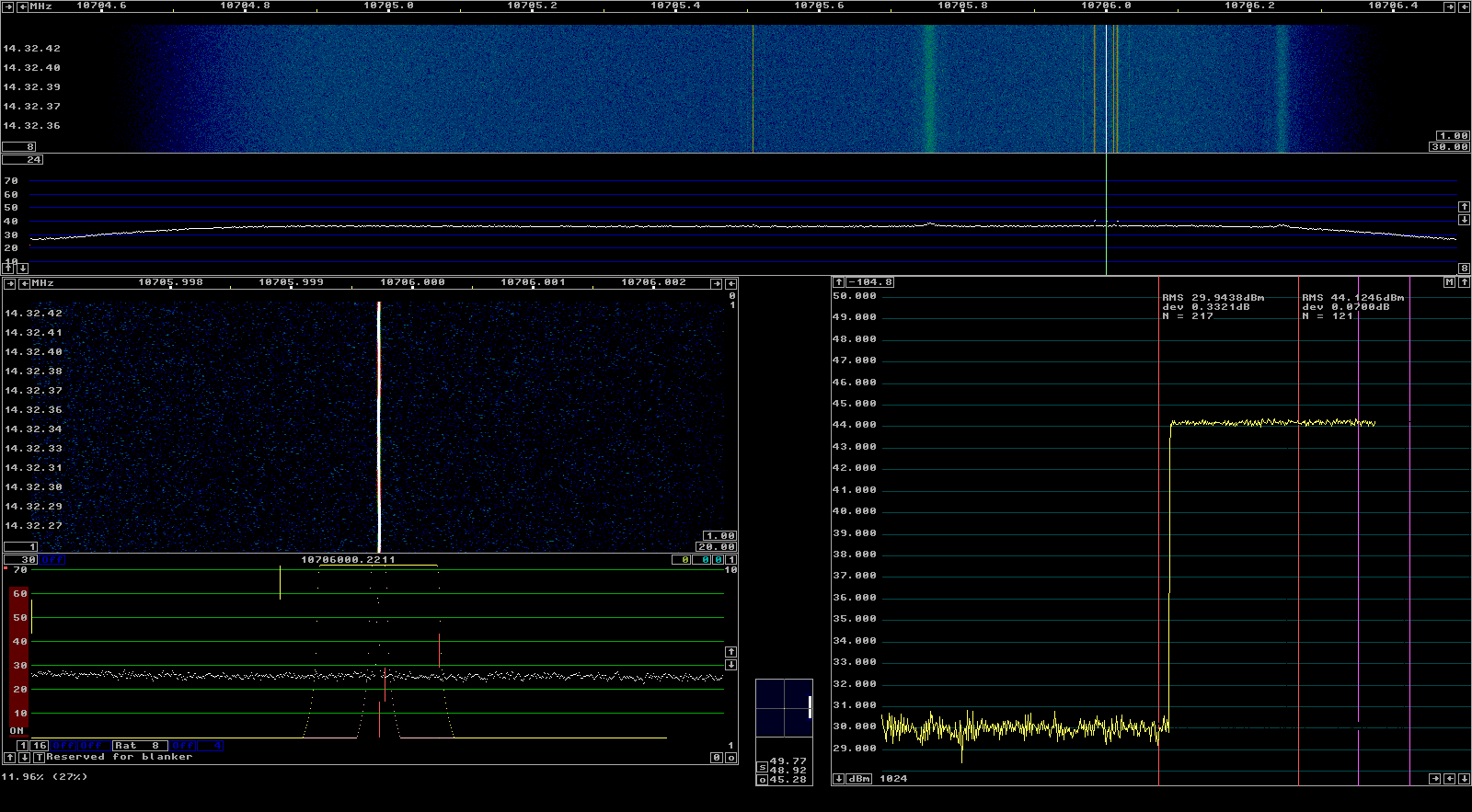
Now that Es’hail 2 is at its operational position, I have taken the time to realign my 95cm offset dish by peaking the signal of the 10706MHz engineering beacon. By doing so, I have gained 4.5dB of SNR and the SNR at which I currently receive the beacon carrier is 44dBHz. This has been measured using Linrad.
One comment