Tag: orbital dynamics

This forms parts of a series of posts showing how to use GMAT to track the DSLWP-B Chinese lunar satellite. In part I we looked at how to examine and validate the tracking files published by BG2BHC using GMAT. It is an easy exercise to use GMAT to perform orbit propagation and produce new tracking files. However, note that the available tracking files come from orbit planning and simulation, not from actual measurements. It seems that the elliptical lunar orbit achieved by DSWLP-B is at least slightly different from the published data. We are already working on using Doppler measurements to perform orbit determination (stay tuned for more information).

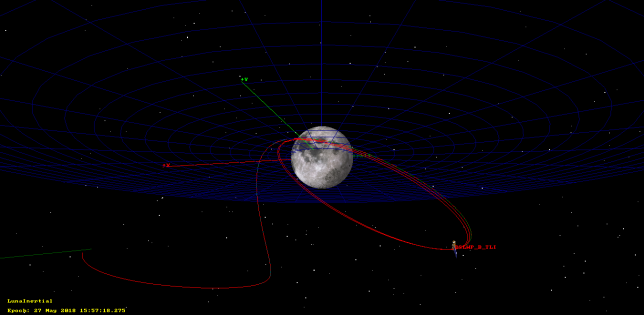
Recall that there are three published tracking files that can be taken as a rough guideline of DSLWP-B’s actual trajectory. Each file covers 48 hours. The first file starts just after trans-lunar injection, and the second and third files already show the lunar orbit. Therefore, there is a gap in the story: how DSLWP-B reached the Moon.

There are at least two manoeuvres (or burns) needed to get from trans-lunar injection into lunar orbit. The first is a mid-course correction, whose goal is to correct slightly the path of the spacecraft to make it reach the desired point for lunar orbit injection, which is usually the lunar orbit periapsis (the periapsis is the lowest part of the elliptical orbit). The second is the lunar orbit injection, a braking manoeuvre to get the spacecraft into the desired lunar orbit and adjust the orbit apoapsis (the highest part of the orbit). Without a lunar orbit injection, the satellite simply swings by the Moon and doesn’t enter lunar orbit.

In this post we will see how to use GMAT to calculate and simulate these two burns, so as to obtain a full trajectory that is consistent with the published tracking files. The final trajectory can be seen in the figure below.

As you may well know, on May 20 a CZ-4C rocket launched from Xichang, China, to deliver Queqiao, the Chang’e 4 relay satellite, to the Moon. Queqiao is a communications relay satellite designed to orbit the L2 point of the Earth-Moon system, supporting the future Chang’e 4 rover that will land on the far side of the Moon. From the L2 point, Queqiao has a good view of both the Earth and the far side of the Moon.

This launch was shared by the DSLWP-A and -B microsatellites, also called Longjiang 1 and 2. These two satellites are designed to be put on a 200 x 9000km lunar orbit and their main scientific mission is a proof of concept of the Discovering the Sky at Longest Wavelengths experiment, a radioastronomy HF interferometer that uses the Moon as a shield from Earth’s interferences.

The DSLWP satellites carry an Amateur radio payload which consists of a 250 baud (or 500 baud) GMSK transmitter which uses \(r=1/2\) or \(r=1/4\) turbo codes, a JT4G beacon, and a camera allowing open telecommand (such as the camera on BY70-1 and LilacSat-1). A year ago, while the radio system was being designed, I wrote a post about DSLWP’s SSDV downlink, which transmits the images taken by the camera.

Wei Mingchuan BG2BHC, who is part of the DSLWP team, has been posting updates on Twitter about the status of the mission. If you’ve been following these closely, you’ll already know that unfortunately radio contact with DSLWP-A was lost on the UTC afternoon of May 22. Since then, all tries to contact the spacecraft have failed (the team will publicly release more information about its fate soon). On the other hand, DSLWP-B has been successfully injected into lunar orbit and is now orbiting the Moon since the UTC afternoon of May 25.

More posts will follow about the radio communications of DSLWP, but this series of posts will deal with the orbital dynamics part of the mission. In this first post, I will look at the tracking files released so far by Wei, which can be used to compute the spacecraft’s position and Doppler.