dslwp – Page 6 – Daniel Estévez

First SSDV transmission from DSLWP-B

As some of you may know, DSLWP-B, the Chinese lunar-orbiting Amateur satellite carries a camera which is able to take pictures of the Moon and stars. The pictures can be downlinked through the 70cm 250bps GMSK telemetry channel using the SSDV protocol. Since an r=1/2 turbo code is used, this gives a net rate of 125bps, without taking into account overhead due to headers. Thus, even small 640×480 images can take many minutes to transfer, but that is the price one must pay for sending pictures over a distance of 400000km.

On Saturday August 3, at 01:27 UTC, the first SSDV downlink in the history of DSLWP-B was attempted. According to Wei Mingchuan BG2BHC, the groundstation at Harbin managed to command the picture download at 436.400MHz a few minutes before the GMSK transmitter went off at 01:30 UTC. A few SSDV frames were received by the PI9CAM radiotelescope at Dwingeloo.

The partial image that was received was quickly shared on Twitter and on the DSLWP-B camera webpage. The PI9CAM team has now published the IQ recording of this event in their recording repository. Here I analyze that recording and perform my own decoding of the image.

DSLWP-B long-term orbit evolution

In my last post I commented that one of the motivations for the periapsis raise manoeuvre of DSLWP-B on July 20 was to prevent the satellite from crashing into the Moon in a few months. When Wei Mingchuan BG2BHC told me this, I found it a bit surprising, since I had the impression that the periapsis had been raising naturally since the satellite was injected in lunar orbit on May 25. Thus, I decided to propagate the orbit for a period of 2 years using GMAT and study the long-term effects in the Keplerian elements.

Update on DSLWP-B eclipse manoeuvre

A few days ago I discussed the manoeuvre performed by DSLWP-B in preparation for the lunar eclipse. The manoueuvre raised the periapsis of DSLWP-B by around 385km. Wei Mingchuan BG2BHC has now informed me that the manoeuvre was performed on 20 Jul 2018 10:47:09.657. There were two motivations for this manoeuvre: first, to avoid eclipse, as I showed in the previous post; second, as Wei tells me, to prevent DSLWP-B from crashing into the Moon in a few months (more on this in a future post).

Wei doesn’t know the delta-v used for the manoeuvre, but estimating it is an easy exercise using GMAT, which is what I will do in this short post. In this simulation I am taking the orbital state for DSLWP-B from the first line of the 20180714 tracking file published in dslwp_dev. I will assume that the manoeuvre was a prograde burn performed at apoapsis that raised the periapsis by 385km. The GMAT script I have used is lunar_eclipse_manoeuvre.script.

First I propagte the orbit to the date mentioned by Wei. I note that the spacecraft is a little short of apoapsis, so I propagate to apoapsis, which happens at 20 Jul 2018 10:49:33.178 UTC. Then I propagate to periapsis and take note of the periapsis radius, which is 3030.91km. Finally, I use GMAT to estimate a burn that will achieve a periapsis radius of 3415.91km using a differential corrector.

The differential corrector finds a delta-v of 17.2m/s. The iterations of the differential corrector can be seen in the figure and text below. A more difficult exercise is to find a burn that stitches together the orbits described by the 20180714 and 20180727a tracking files. I will leave this as an exercise for the reader. Something very similar was done in DSLWP-B’s journey to the Moon: part II.

Differential corrector solving for the periapsis raise burn

DSLWP-B and the lunar eclipse

As you may well know, last Friday 27th July there was a total lunar eclipse. This is an interesting event for lunar-orbiting spacecraft such as DSLWP-B. In fact, depending on the spacecraft’s orbit, it may also pass through the Earth’s umbra or penumbra. Here I look at the trajectory taken by DSLWP-B during the eclipse.

Comparison of DSLWP-B orbit determination with tracking files

In the last post I compared the results of my orbit determination for DSLWP-B using one lunar month of Doppler data with the observations in the VLBI experiment done on June 10. In this post I will compare my orbit determination with the tracking files published by Wei Mingchuan BG2BHC in gr-dslwp. These tracking files are produced from the orbit determination performed by the Chinese Deep Space Network using two-way S-band Doppler measurements.

The tracking files contain a listing of the position \(x\) and velocity \(v\) vectors for DSLWP-B in ECEF coordinates. The entries are given at intervals of one second. The tracking files can be used directly to compute Doppler as received in a groundstation. In fact, if the ECEF coordinates of the groundstation are \(x_0\), then \(R = \langle x – x_0, v\rangle/\|x-x_0\|\) is the range-rate, and so the Doppler can be computed as \(D=-fR/c\), where \(f\) is the downlink frequency and \(c\) is the speed of light in vacuum. Here I have used this method to compute the Doppler according to the tracking files.

All the tracking files published so far have been considered in this study, except for the first two, which contained an incorrect anomaly at epoch. The figure below shows the residuals between the Doppler measurements made by Scott Tilley VE7TIL and my orbit determination (called “new elements”) and each of the tracking files. It seems that the residuals are quite similar.

The figure below shows the difference between the Doppler according to each of the tracking files and the Doppler predicted by my orbit determination.

It seems that the match is quite good for the central days, but not so good towards the edges. My orbit determination is numerically propagated from a single set of elements at MJD 28264.5 for the whole period, while the tracking files probably use different sets of elements that are propagated numerically over a few days only. Therefore it might happen that my orbit determination is affected by some accumulative error due to numerical integration or an inaccuracy in the force model.

Validation of DSLWP-B orbit determination using VLBI observations

In my last post I presented my orbit determination of DLSWP-B using one lunar month of S-band Doppler measurements made by Scott Tilley VE7TIL. In this post, I will use the delta-velocity measurements from the VLBI experiment on 2018-06-10 to validate my orbital elements.

In the figures below, I compare between the sets of data: The old elements, obtained in this post:

DSLWP_B.SMA = 8762.40279943
DSLWP_B.ECC = 0.764697135746
DSLWP_B.INC = 18.6101083906
DSLWP_B.RAAN = 297.248156986
DSLWP_B.AOP = 130.40460851
DSLWP_B.TA = 178.09494681

The new elements obtained in my last post:

DSLWP_B.SMA = 8765.95638789
DSLWP_B.ECC = 0.764479041563
DSLWP_B.INC = 23.0301858287
DSLWP_B.RAAN = 313.64185464
DSLWP_B.AOP = 113.462338342
DSLWP_B.TA = 178.5519212

The elements obtained from the 20180610 tracking file published by Wei Mingchuan BG2BHC in dslwp_dev. This tracking file contains a list of ECEF position and velocity vectors for DSLWP-B. The first entry is taken as the orbital state and the orbit is propagated in GMAT, as done in this post. It would also be possible to calculate the delta-velocity directly from the ECEF data, but the results would be fairly similar and I already have a script to do it with GMAT orbit propagation.

A degree 2 polynomial fit to the VLBI observations. It turns out that the delta-velocity during the VLBI experiment can be approximated fairly well by a parabola, so it makes sense to use this as a reference. Note that this also implies that this set of delta-velocity measurements alone would be insufficient to perform orbit determination, as a degree 2 polynomial gives us 3 coefficients, while we would need to determine 6 parameters for the orbital state. Adding delta-range would only give us an extra variable, so orbit determination using VLBI would need several sets of measurements well space in time so that the orbit can be observed at different anomalies.

The figures below show a comparison between the four sets of data and the VLBI measurements.

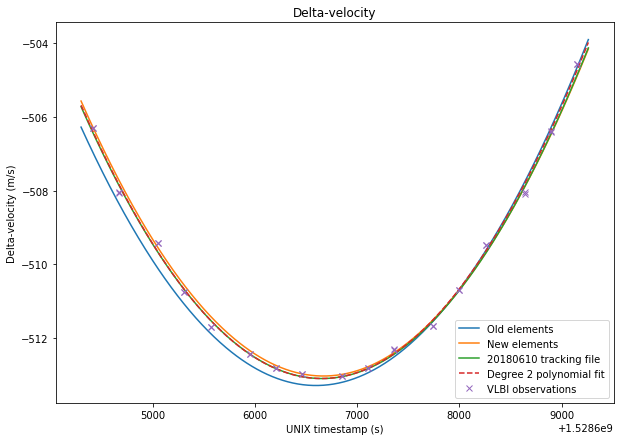
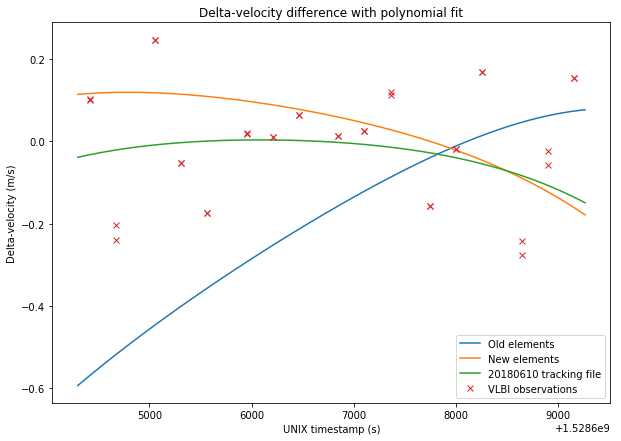
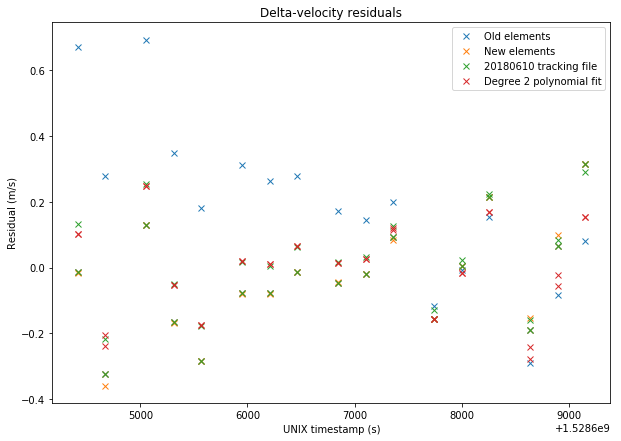
The RMS errors are respectively 0.248m/s for the old elements, 0.167m/s for the new elements, 0.156m/s for the tracking file, and 0.137m/s for the polynomial fit. Thus, we see that the newer elements represent a good improvement over the older elements. The tracking file gives a slightly better result than the new elements. However, the new elements should give good results over a long time span of over 20 days, as we have seen in the previous post, while the orbital parameters derived from the tracking files tend to change often.

The Jupyter notebook used to make these calculations has been updated in here.

DSLWP-B first month in orbit

DSLWP-B has now been for more than a month in lunar orbit, since the orbital injection was made on May 25. Scott Tilley VE7TIL has sent me his latest batch of S-band Doppler measurements, including data for all this first lunar month. Having a complete lunar month of data is interesting for orbit determination purposes, since it gives observability of the orbit from all possible right ascension angles.
I have run my orbit determination with the new data.

DSLWP-B GMSK detector

Following the success of my JT4G detector, which I used to detect very weak signals from DSWLP-B and was also tested by other people, I have made a similar detector for the 250baud GMSK telemetry transmissions.

The coding used by the DSLWP-B GMSK telemetry follows the CCSDS standards for turbo-encoded GMSK/OQPSK. The relevant documentation can be found in the TM Synchronization and Channel Coding and Radio Frequency and Modulation Systems–Part 1: Earth Stations and Spacecraft blue books.

The CCSDS standards specify that a 64bit ASM shall be attached to each \(r=1/2\) turbo codeword. The idea of this algorithm is to correlate against the ASM (adequately precoded and modulated in GMSK). The ASM spans 256ms and the correlation is done as a single coherent integration. As a rule of thumb, this should achieve a reliable detection of signals down to around 12dB C/N0, which is equivalent to -12dB Eb/N0 or -22dB SNR in 2500Hz. Note that the decoding threshold for the \(r=1/2\) turbo code is around 1.5dB Eb/N0, so it is much easier to detect the GMSK beacon using this algorithm than to decode it. The difficulty of GMSK detection is comparable to the difficulty of JT4G decoding, which has a decoding threshold of around -23dB SNR in 2500Hz.

Here I explain the details of this GMSK ASM detector. The Python script for the detector is dslwp_gmsk.py.

DSLWP-B detected with 7 element yagi

Yesterday I tried to detect DSLWP-B using my 7 element Arrow satellite yagi. The test schedule for DSLWP-B was as follows: active between 21:00 and 23:00 UTC on 2018-06-22. GMSK telemetry transmitted both on 435.4MHz and 436.4MHz. JT4G only on 435.4MHz every 10 minutes starting at 21:10. The idea was to record the tests with my equipment and the run my JT4G detector, which should be able to detect very weak signals. Today I have processed the recorded data and I have obtained a clear detection of one of the JT4G transmissions (albeit with a small SNR margin). This shows that it is possible to detect DSLWP-B with very modest equipment.

DSLWP-B first JT4G test

Yesterday, between 9:00 and 11:00, DSLWP-B made its first JT4G 70cm transmissions from lunar orbit. Several stations such as Cees Bassa and the rest of the PI9CAM team at Dwingeloo, the Netherlands, Fer IW1DTU in Italy, Tetsu JA0CAW and Yasuo JA5BLZ in Japan, Mike DK3WN in Germany, Jiang Lei BG6LQV in China, Dave G4RGK in the UK, and others exchanged reception reports on Twitter. Some of them have also shared their recordings of the signals.

Last week I presented a JT4G detection algorithm intended to detect very weak signals from DSLWP-B, down to -25dB SNR in 2500Hz. I have now processed the recordings of yesterday’s transmissions with this algorithm and here I look at the results. I have also made a Python script with the algorithm so that people can process their recordings easily. Instructions are included in this post.