Yesterday I did an analysis of the image taken and downloaded during the test run for the imaging of the solar eclipse shadow on the Earth with DSLWP-B on July 2. Only one of the six images taken to validate the camera exposure and pointing and orbit errors was downloaded yesterday. The window to download the remaining images was during today’s activation of the Amateur payload between 05:30 and 07:30 UTC.
Three images were downloaded today, with a few missing chunks. Moreover, Wei Mingchuan BG2BHC has sent me better ephemeris, which give a more accurate prediction of the orbit both on the June 30 test run and on the eclipse imaging run on July 2. This post is an analysis of the images downloaded today.
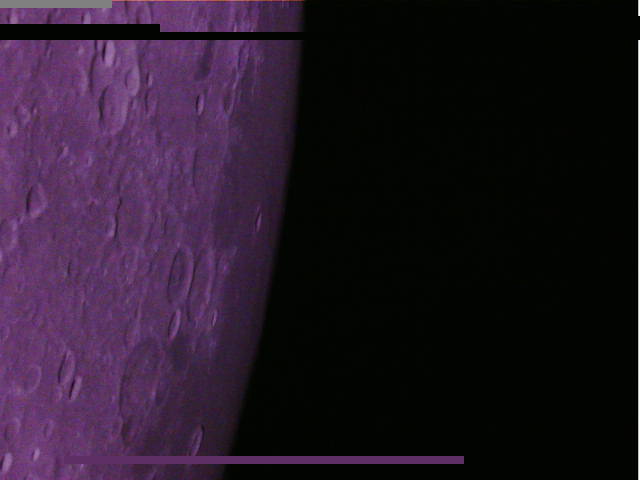
Images 0xDD, 0xDE and 0xDB from the series of six test run images (0xD9 – 0xDE) were downloaded from DSLWP-B, using the groundstation at Dwingeloo. These are shown below. As it can be seen in the captions, most of the time the satellite was kept transmitting an image, so an efficient use was made of the two hour activation window.


In parallel, the GMSK to JT4G repeater onboard DSLWP-B was used to make a QSO between BY2HIT, the Harbin Institute of Technology Amateur radio club, and Reinhard Kuehn DK5LA. This is the first ever Amateur radio QSO made through a lunar orbiting repeater. It was reported by Wei in the tweet shown below.
Using the GMSK to JT4G repeater is not easy, in terms of the signal power needed for the uplink. There were plans to make a QSO between BY2HIT and Reinhard since many months ago, but previous attempts didn’t work out. My congratulations to the people at both sides of the QSO, who have achieved it a month before DSLWP-B crashes against the lunar surface.
The GMSK to JT4G repeater works by sending commands to the satellite which embed a 13 character message, using the same frequency and a similar protocol to the one used to command the camera and other satellite functions. The precise definition of this mode is a 7.8125 baud FSK modulation with a shift of 394.53125Hz. Each FSK tone is “spread” with a 250 baud GMSK 32 bit syncword. The CCSDS 32 bit syncword is used to mark the beginning of a packet, and a Reed-Solomon (64,32) code is used for FEC, together with CCSDS scrambling. Such a message takes a bit longer than one minute to transmit. The uplink is in the 2m Amateur satellite band.
The repeater downlink is the usual JT4G downlink of DSLWP-B in the 70cm Amateur satellite band. The 13 character messages sent in the uplink command replace the usual JT4G telemetry, being repeated as a free-form JT4G message. In the case of this QSO, the B1 radio at 436.400MHz was used. This radio was also used to transmit the images using GMSK SSDV.
I have updated my Jupyter notebook to measure the angle between the centre of the image and the rim of the Moon in each of the images downloaded today. Angles of -1.33º, 1.31º and 4.70º have been obtained for images 0xDD, 0xDE and 0xDA respectively.
Since I suspected that the usual ECEF cartesian ephemeris that Wei computes with STK could be giving some problems, he has been kind enough to share Moon centred ICRF Keplerian ephemeris. These are shown below in GMAT. The only difference from the ephemeris that Wei sent me is that Wei uses a mean anomaly of 164.619 degrees, whereas GMAT needs the true anomaly. The true anomaly below has been computed from this mean anomaly and the eccentricity.
DSLWP_B.DateFormat = UTCGregorian; DSLWP_B.Epoch = '28 Jun 2019 03:00:00.000'; DSLWP_B.CoordinateSystem = LunaICRF; DSLWP_B.DisplayStateType = Keplerian; DSLWP_B.SMA = 8704.163; DSLWP_B.ECC = 0.690187; DSLWP_B.INC = 44.672; DSLWP_B.RAAN = 71.711; DSLWP_B.AOP = 68.006; DSLWP_B.TA = 176.09042928330206;
I have redone the graphs in this post using these ephemeris. The results are shown below.
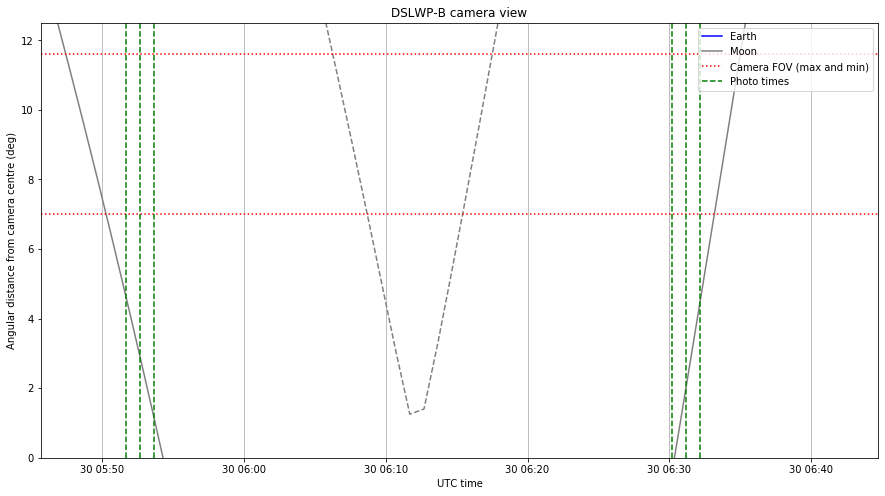
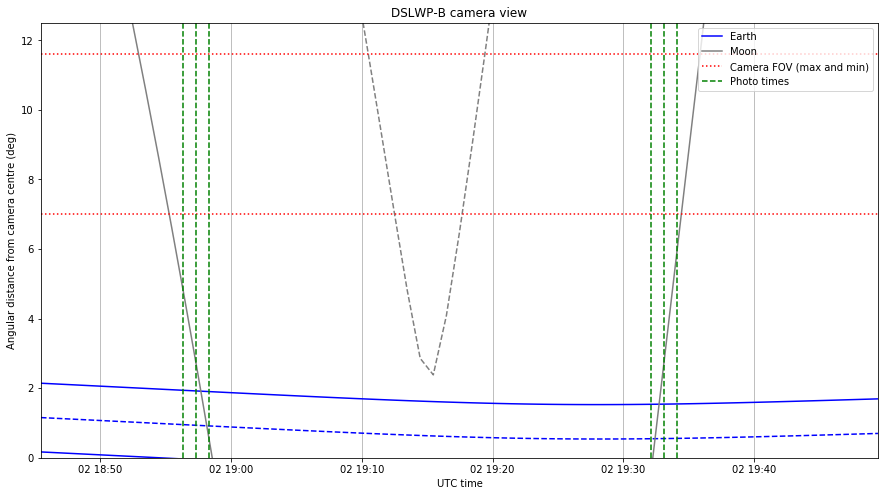
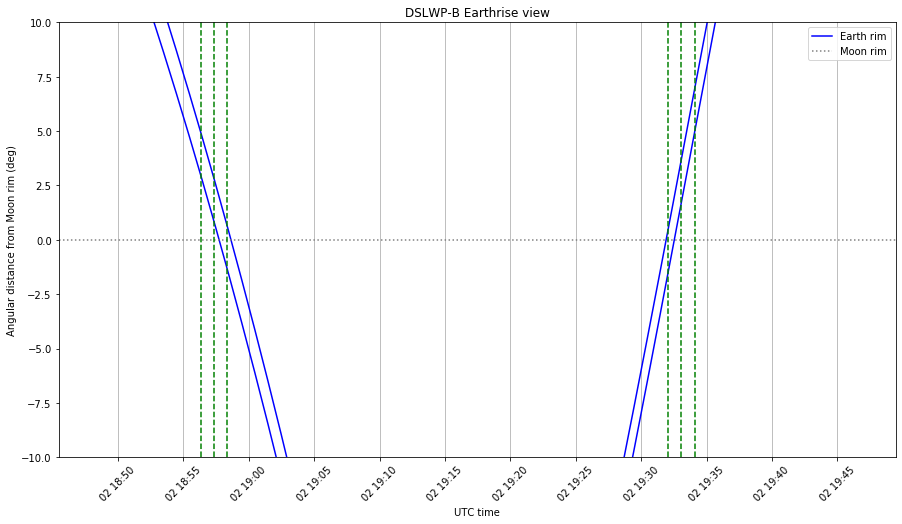
It is interesting to compare these figures with the figures computed with the ECEF ephemeris. The times when the Moon passes through the centre of the image have changed slightly, and now match much better the times that Wei proposed for taking the images. Therefore, I think that using the ICRF ephemeris in GMAT we get results that are very similar to what Wei is getting in STK.
Using this data, we can compute the difference in the separation of the Moon rim from the centre of the image as measured in the images and as predicted by the ephemeris. This is done in the camera view Jupyter notebook. We obtain values of 3.53º and 3.54º for images 0xDB and 0xDC, which were taken as the Moon hid the centre of the image, and -3.34º and -3.19º for images 0xDD and 0xDE, which were taken as the Moon moved again out of the centre of the image.
Note the different signs in these values. As the Moon was moving towards the centre of the image, we have positive differences, meaning that the Moon was further from the centre of the image than what predicted by the ephemeris. As the Moon was moving away from the centre of the image, the Moon was closer to the centre of the image than what predicted.
These results are consistent with the idea I introduced in the previous post that the satellite is somewhat earlier on its orbit than what is predicted by the ephemeris. On the other hand, the difference between the ephemeris prediction and the images could be caused by a pointing error. However, assuming that the satellite didn’t change its attitude noticeably throughout the test run, a pointing error would contribute with the same sign to all the images.
Taking into account the speed at which the Moon moves through the field of view, as predicted by the ephemeris, and assuming no pointing error, we get a temporal error in the along-track component of the orbit of -120, -118, -81 and -77 seconds on each of the images.
Even though we have assumed that there can be a pointing error of up to 3.25º, which represents a temporal error between 78 and 113 seconds, the data seems to suggest that most of the discrepancy between the images and the ephemeris prediction is caused by an along-track error in the orbit. A pointing error of around 1.4º towards the left of the image could explain the relatively large difference of along-track errors seen when the Moon moves into the image (around -120 seconds) and when the Moon moves away from the image (around -80 seconds). In this case, the real along-track error would be on the order of -100 seconds.
Even though I reckon that these images are not a very precise tool for measuring the orbit, my guess is that DSLWP-B is between one and two minutes earlier on its orbit than what predicted by the ephemeris. This is not much of a problem for tomorrow’s eclipse imaging, because several images will be taken and there is some margin for error. The only risk is that in some of the three images taken as the satellite reappears from behind the Moon, the Earth might still be hidden. Additionally, Wei tells us that it is not so easy to change the programmed imaging times at this point, so let’s hope for the best tomorrow.
Update 2019-07-02: Actually there is an important mistake in my reasoning above. A pointing error wouldn’t give the same sign to the error in all the images. In fact, the differences we are seeing between the images and the ephemeris prediction can be explained by a pointing error of approximately 3º towards the left of the image (so that the satellite looks slightly to the retrograde direction). It is not easy to distinguish such a pointing error from the satellite being slightly early on its orbit. The radio occulation measurements done by Scott Tilley on 2019-07-01 22:29 UTC suggest that the ephemeris I have used here match the orbit of the satellite well, only allowing an error on the order of 10 seconds in the along-track component of the orbit. Thus, I withdraw my conclusion that the satellite is approximately 100 seconds earlier on its orbit and conclude that most of the error seen in the images studied in this post must be caused by a pointing error, rather than an ephemeris error.
6 comments