JT4G detection algorithm for DSLWP-B

Now that DSLWP-B has already been for 17 days in lunar orbit, there have been several tests of the 70cm Amateur Radio payload, using 250bps GMSK with an r=1/2 turbo code. Several stations have received and decoded these transmissions successfully, ranging from the 25m radiotelescope at PI9CAM in Dwingeloo, the Netherlands (see recordings here) and the old 12m Inmarsat C-band dish in Shahe, Beijing, to much more modest stations such as DK3WN‘s, with a 15.4dBic 20-element crossed yagi in RHCP. The notices for future tests are published in Wei Mingchuan BG2BHC’s twitter account.

As far as I know, there have been no tests using JT4G yet. According to the documentation of WSJT-X 1.9.0, JT4G can be decoded down to -17dB SNR measured in 2.5kHz bandwidth. However, if we don’t insist on decoding the data, but only detecting the signal, much weaker signals can be detected. The algorithm presented here achieves reliable detections down to about -25dB SNR, or 9dB C/N0.

This possibility is very interesting, because it enables very modest stations to detect signals from DSLWP-B. In comparison, the r=1/2 turbo code can achieve decodes down to 1dB Eb/N0, or 25dB C/N0. In theory, this makes detection of JT4G signals 16dB easier than decoding the GMSK telemetry. Thus, very small stations should be able to detect JT4G signals from DSLWP-B.

As described in the WSJT-X documentation, the JT4 family uses 4FSK at 4.375baud. A total of 206 symbols are transmitted over the 47.09s that a complete message lasts. A pseudo-random 206 bit sync vector is used for time and frequency synchronization. The sync vector is the following (note that there is an error in the WSJT-X documentation):

000110001101100101000000011000000000000101101101011111010001
001001111100010100011110110010001101010101011111010101101010
111001011011110000110110001110111011100100011011001000111111
00110000110001011011110101

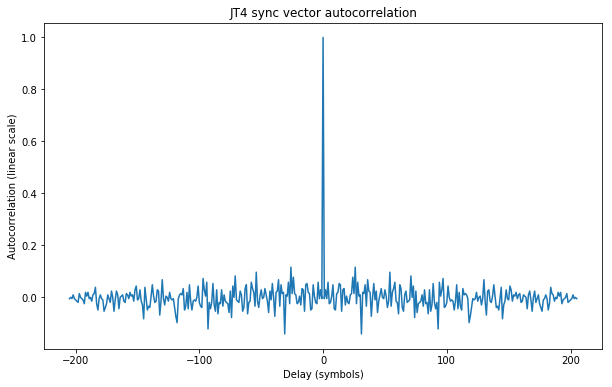
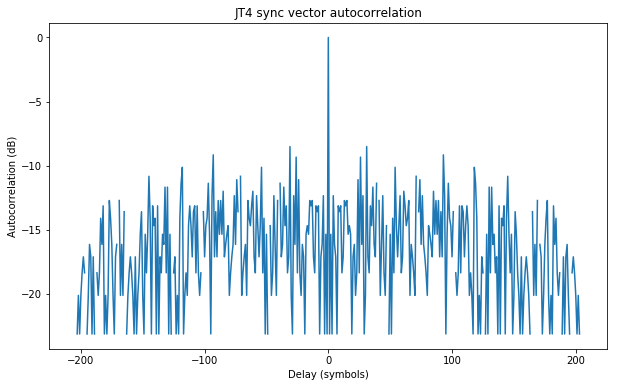
The autocorrelation function of this sequence is shown below, both in a linear scale and in dB units.

The autocorrelation function has rather strong sidelobes of around -8dB. These could be reduced by using a well designed sync vector. However, the strength of the sidelobes is not important for any reasonable use of the JT4 or other similar modes.

A JT4 message contains 72 information bits, encoded using a k=32, r=1/2 convolutional code with zero-tailing, yielding 206 FEC symbols. These FEC symbols are transmitted together with the sync vector as follows: the sync vector symbol is encoded as the least significant bit of the 4FSK symbol and the FEC symbol is encoded as the most significant bit of the 4FSK symbol. In other words, if we number the four FSK tones as \(T_0\), \(T_1\), \(T_2\), \(T_3\), then the sync vector symbol chooses between \(\{T_0, T_2\}\) and \(\{T_1, T_3\}\), and the FEC symbol chooses between \(\{T_0, T_2\}\) and \(\{T_1, T_3\}\). Therefore, 50% of the message power is devoted to synchronization. This enables us to perform detections at a very low SNR.

The idea of the synchronization algorithm is to compute, for each symbol \(n\) and each tone \(j\) the corresponding power \(P(T_{j,n})\) and compute the sequence\[x_n = P(T_{1,n}) + P(T_{3,n}) – P(T_{0,n}) – P(T_{2,n}).\]
Then the sequence \(x_n\) is correlated against the bipolar sequence \(s_n\) obtained from the sync vector. This correlation gives a strong peak at the correct delay, regardless of what data has been transmitted.

This is the algorithm idea. To transform it into a complete algorithm, we must perform some form of frequency and time synchronization. First, an FFT is applied to the signal. The FFT size is chosen to yield a frequency resolution of 4.375Hz, so that a single 4FSK symbol fits exactly in a Fourier transform. This limits the choice of the the sample rate to multiples of 35Hz. To provide finer time synchronization, overlapping FFT transforms are made, using a 50% of overlap. We denote as \(f_{k,n}\) the \(k\)-th frequency bin of the \(n\)-th FFT.

The tone separation for JT4G is \(S=72\) bins. We compute\[x_{k,n} = |f_{k+S,n}|^2 + |f_{k+3S,n}|^2 – |f_{k,n}|^2 + |f_{k+2S,n}|^2.\] Finally, for each \(k\), the sequences \(x_{k,2j}\) and \(x_{k,2j+1}\) are correlated against \(s_j\). This yields a correlation peak for the \(k\) corresponding to the frequency of the lowest tone \(T_0\) and the delay \(j\) corresponding to the start of the JT4G message.

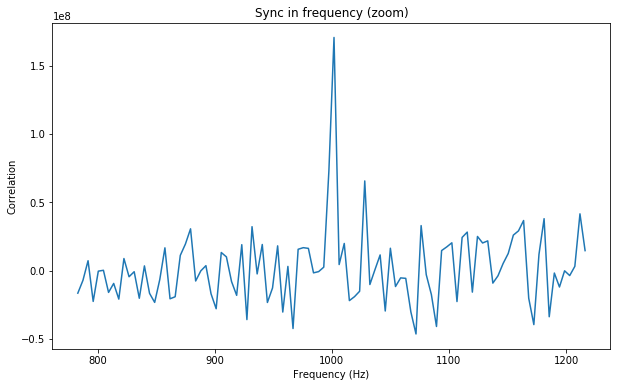
The figures below show the correlations for a -25dB SNR signal generated with jt4sim (see this post for more information on simulating WSJT-X signals).

The calculations used in this post have been performed in this Jupyter notebook. Let’s stay tuned for the first DSLWP-B JT4G tests to check the performance of this algorithm with real recordings.

The algorithm presented here assumes no previous knowledge of the data transmitted in the JT4G message. Perhaps DSLWP-B transmits always the same data and this can be used to improve even further the sensitivity of this detection algorithm.