In my last post about Tianwen-1, I explained how on 2021-02-23 the spacecraft would enter an orbit with a period of 2 Mars sidereal days. This would give a repeating ground track with periapsis passages over the intended landing site in Utopia Planitia. Almost one month has passed since then and AMSAT-DL has continued to receive telemetry state vectors every day with the Bochum 20 meter antenna. This data allows us to study the orbit in detail, including orbit perturbations and any station-keeping manoeuvres that are done to maintain the orbit. This post is my first analysis of the current orbit.
For this study, the main idea is to load up the state vector data in Python and use GMAT’s Python API to propagate the trajectory to fill in the gaps in the data, so as to obtain a continuous trajectory. This is my first time using GMAT’s API, but besides the documentation, which is perhaps a bit hard to read, there are several good example Python scripts and Jupyter notebooks in the api/ folder of GMAT-R2020a, so by taking these as a reference, I’ve been able to quickly put together the code to do what I wanted.
By using GMAT’s propagator only to fill in the gaps between the state vectors, we don’t need to take much care about whether the GMAT force model accurately captures all the orbit perturbations, or whether the numerical integrator errors tend to accumulate. The trajectory will always snap back to the state vectors, and the largest gap we have to fill in is on the order of one day. This is a task where the API is ideal. We are going to iterate over the list of state vectors, adding new elements obtained by propagation to fill in the gaps. Making a GMAT script and calling GMAT on the fly for each of these gaps would be very cumbersome. Besides propagation, the GMAT API is used to convert the Mars inertial coordinates into Mars body fixed coordinates, since we’re mainly interested in studying the ground track.
The figure below shows the ground track obtained by this method. In blue we show the state vector data that was received by Bochum, while the propagated data to fill in the gaps is depicted in grey. The periapsis passage is the vertical trace around 110ºE. We see that Bochum hasn’t ever collected data around periapsis, so propagation is essential to study what happens.
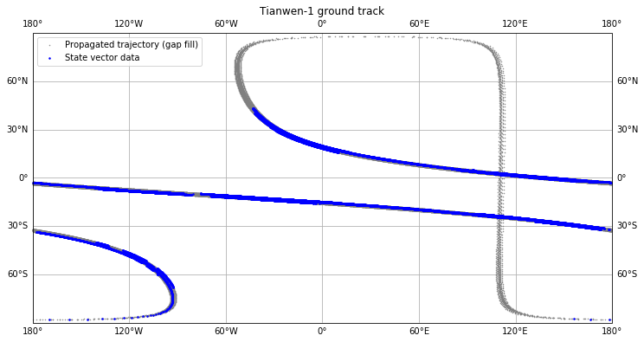
Here we see a better look at which data has been received as telemetry state vectors and which data has been propagated. The periapsis and apoapsis passages are also detected and marked, since we will be using these later.
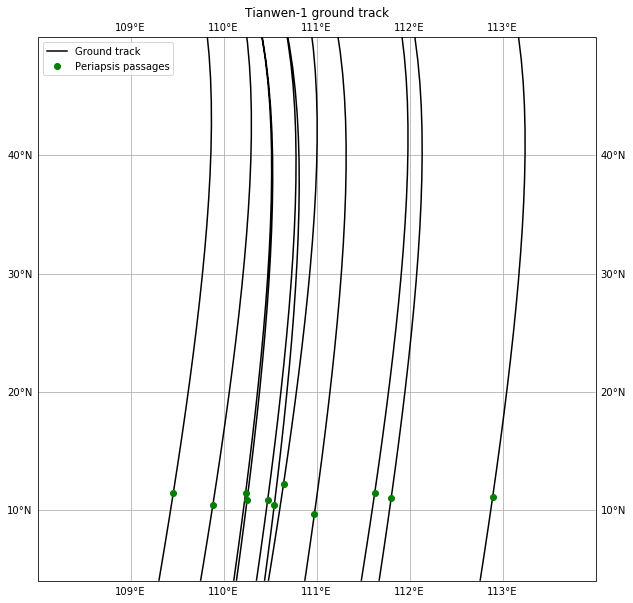
The following shows a zoom to the periapsis passages of the ground track. Note that the aspect ratio of this map is not 1:1, since only a few degrees of longitude are shown to exaggerate the east-west drift of the ground track, which is nearly 4 degrees.
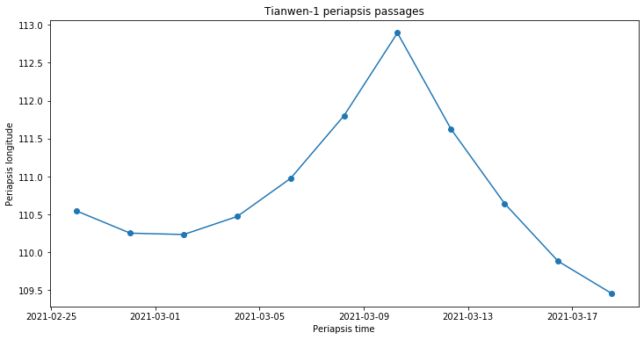
The next figure shows more clearly the drift of the ground track by plotting the longitude of each periapsis passage versus time. The curve looks like a parabola. At some time around 2021-03-10 there is a station-keeping manoeuvre to prevent the orbit from drifting too far east and the orbit starts drifting back west in a parabolic manner.
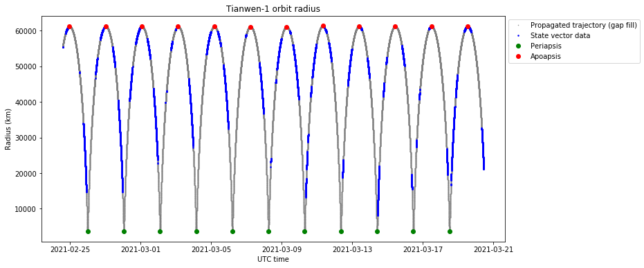
The reason for this parabolic drift is the change in orbit period, which is plotted below by showing the interval between successive periapsis passages. This is represented as the excess in seconds from the nominal orbital period of 2 Mars sidereal days.
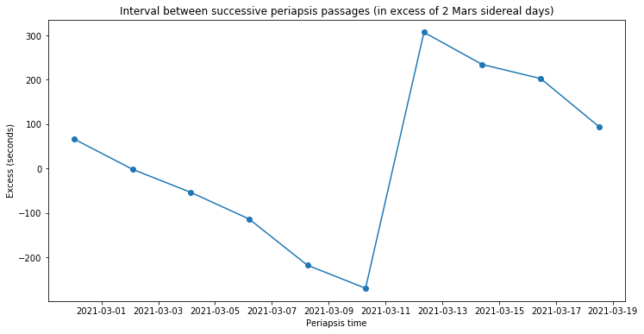
We see that the orbit period decreases linearly with time until the station-keeping manoeuvre, which is a small burn at periapsis to raise the apoapsis and make the orbit period larger than nominal again. The longitude drift of the ground track is basically the integral of this period excess, with the correct sign: if the period is larger than nominal, the orbit will drift west. Karl Meinzer DJ4ZC says that the reason for the decrease in the orbit period is probably the atmospheric drag during the periapsis passages. In fact he’s been doing some calculations to estimate this effect, but we lack a good model for the Mars high-altitude atmosphere.
The next figure shows the evolution of the apoapsis radius, where we see the same linear decrease over time. The first apoapsis after the station-keeping manoeuvre seems to be too high. This is probably caused by the state vectors not being too accurate after a manoeuvre has been performed. They would contain the trajectory resulting from a prediction of the burn performance, rather than the burn itself. After one or two days, the achieved orbit is computed and uploaded by the Chinese DSN.
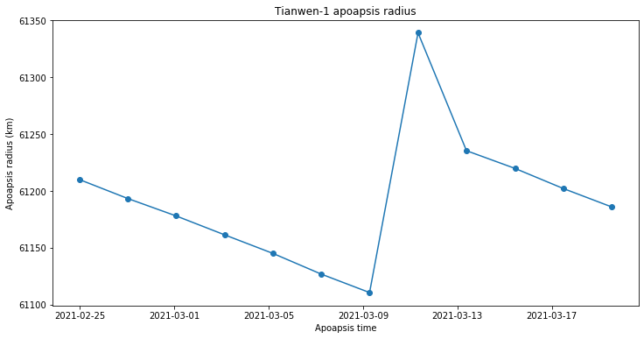
In summary, we’ve seen that the period of the reconnaissance orbit of Tianwen-1 tends to decrease over time, most likely due to atmospheric drag at periapsis. This makes the orbit’s ground track drift east. As a consequence, a station-keeping manoeuvre is needed every 2 or 3 weeks to increase the orbit period and make the ground track drift back west.
The calculations and plots for this post were done in this Jupyter notebook.
4 comments