In my last post, I detailed the DSLWP-B camera planning for the beginning of November. There, I used orbital state taken from the 20181027 tracking file to compute good times to take images of the Moon and the Earth, especially looking for an Earthrise-like image.
Now that the planned dates are closer, it is good to rerun the calculations with a newer orbital state. It turns out that there has been an important change in the mean anomaly, which shifts all the predictions by a few hours.
Wei Mingchuan BG2BHC has shared with me the following orbital state:
1 Nov 2018 01:00:00.000 UTCG 8944.73 km 0.693093 25.436 deg 275.829 deg 182.432 deg 341.22 deg
This is a Keplerian state in a Moon-centred ICRF system. The order of the parameters is semimajor axis, eccentricity, inclination, right-ascension of ascending node, argument of perigee, and mean anomaly at epoch.
The first I did to validate this orbital state and compare it with the 20181027 tracking file was to propagate the state from the tracking file until the epoch of the Moon-centred state, obtaining the following Keplerian parameters in GMAT:
SMA = 8967.6642920312 km
ECC = 0.6916035872391
INC = 25.355035586614 deg
RAAN = 275.99883173444 deg
AOP = 182.19446134707 deg
TA = 218.41134738746 deg
MA = 297.23739933521 deg
EA = 258.41824752311 deg
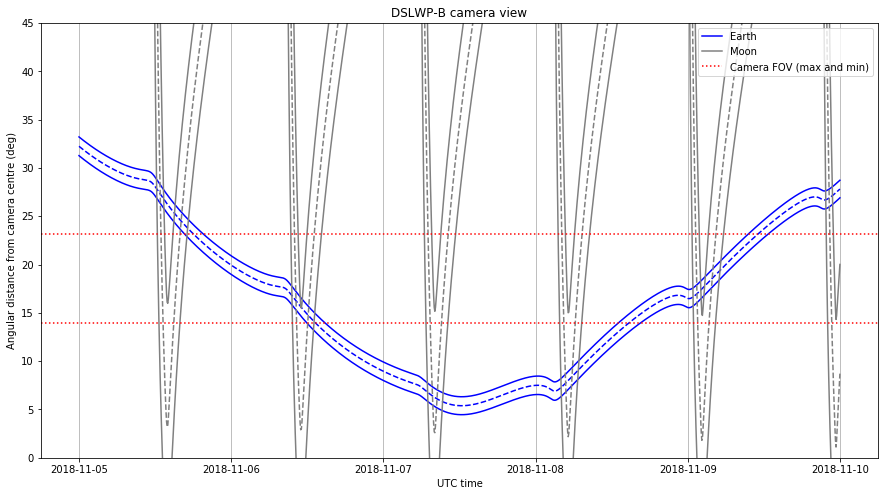
We see that most of the orbital parameters are very similar. The SMA however is 23km smaller in Wei’s state. Accordingly, the MA in Wei’s state is larger. Indeed, it is 83 degrees larger, which at an orbital period of 21.17 hours, corresponds to 4.9 hours. Thus, we expect that all the events that we predicted in the previous post will happen a few hours earlier according to Wei’s state.
After validating Wei’s state, I have rerun my GMAT simulation using it. It is important to note that GMAT needs true anomaly instead of mean anomaly when specifying a Keplerian state, so I have made a small Python function to convert MA to TA.
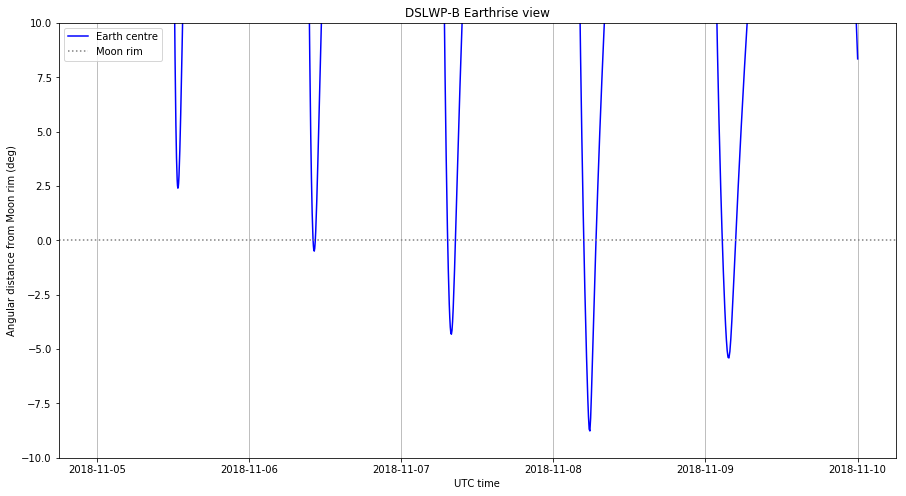
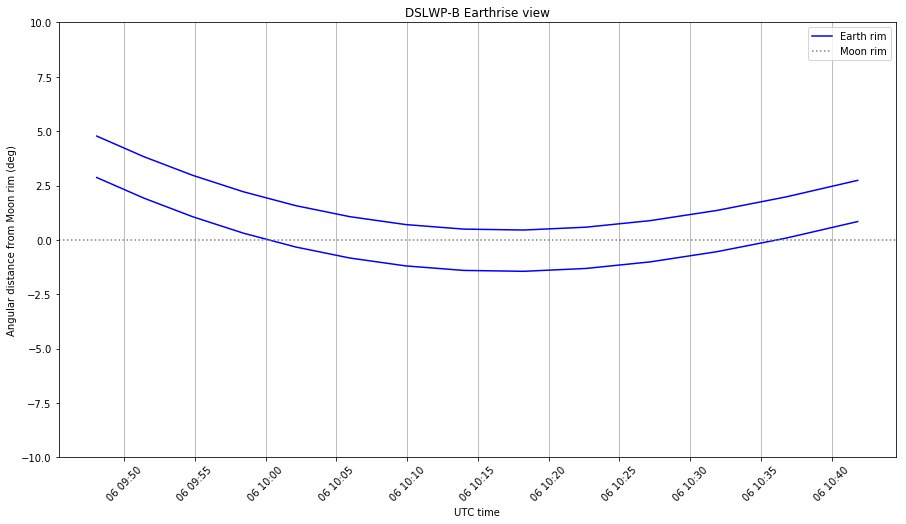
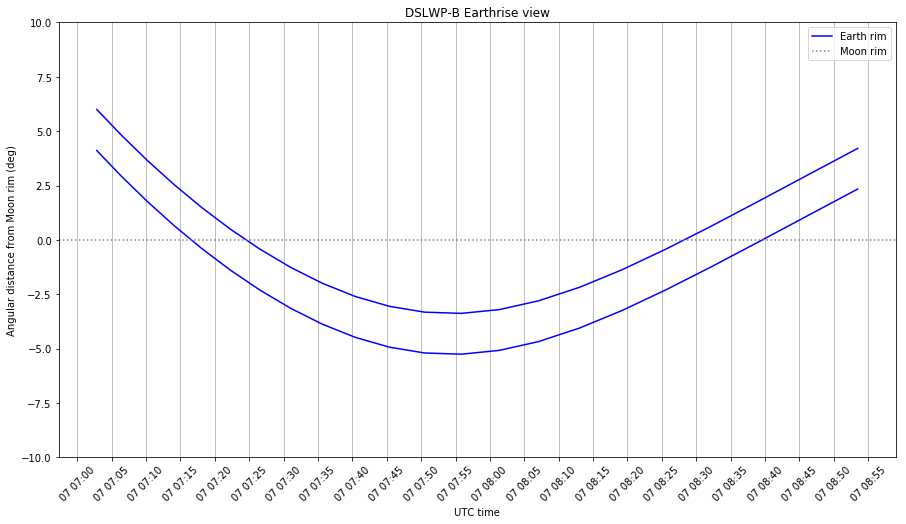
The updated Jupyter notebook is here. These are the graphs it produces. Note that the Earthrise events happen approximately 3 hours earlier than what I predicted in the previous post.
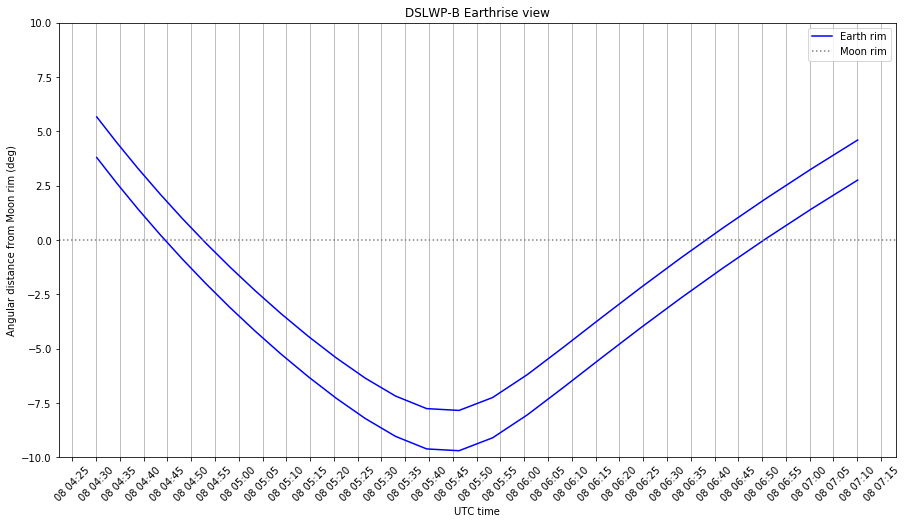
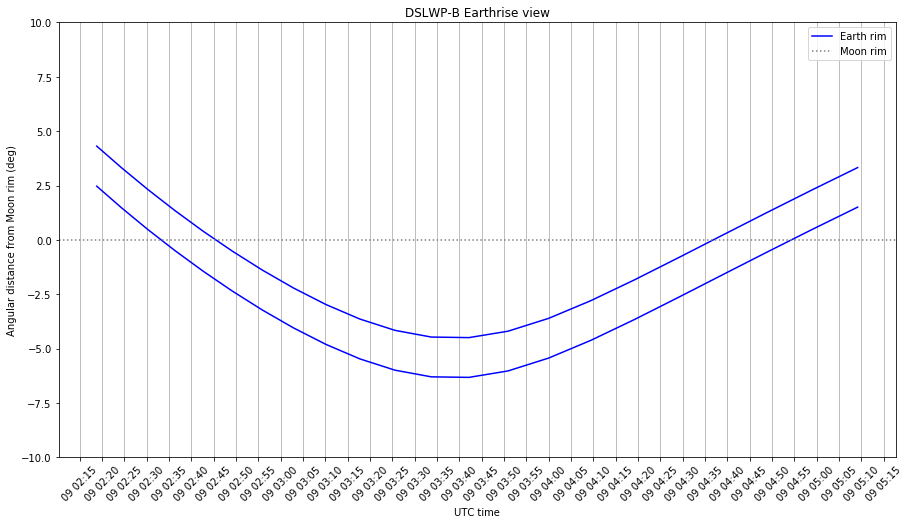
2 comments