Today at 9:00 UTC Tianwen-1 made its plane change manoeuvre, as reported by Xinhua. Yesterday I showed my planning for this manoeuvre. Shortly after the spacecraft returned to the high gain antenna after the manoeuvre, the Bochum 20m antenna operated by AMSAT-DL received state vectors with the new trajectory. These state vectors allow us to calculate the timestamp of the burn and the delta-V vector, as I have done in other occasions. It is convenient to remark that the state vectors that we are seeing right now are probably a prediction. In the next few days we will see updates in the trajectory as the Chinese DSN measures the effects of the actual burn and updates the onboard ephemerides.
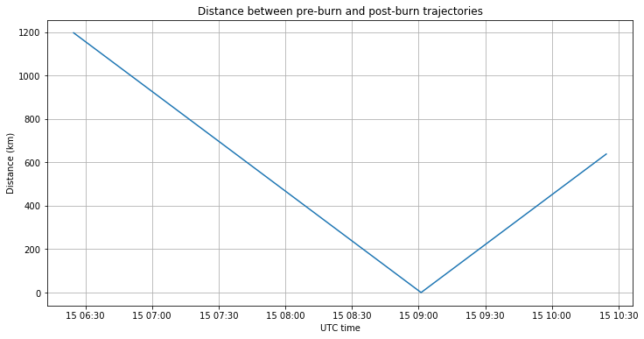
The figure below shows the distances between the pre-burn and post-burn trajectories. Finding the minimum of this curve is the method that I use to find the time of the burn. The minimum is attained at 09:01:05 UTC. Since the burn duration was slightly longer than 2 minutes, the report of the burn start at 09:00 UTC seems quite right.
The delta-V vector was, in Mars body inertial coordinates and m/s,
[86.471, 28.957, 89.190]
The magnitude of this vector is 127.556 m/s.
As I remarked in the update at the end of my previous post, it turns out that we had underestimated the initial fuel of Tianwen-1 by some 900 kg. In that post the plane change took 146 kg of fuel, leaving 45 kg of remaining fuel. Therefore, I have now estimated that the amount of fuel before the plane change was 1100 kg, and that the spacecraft’s dry mass is 2500 kg. This gives a burn time of 150 seconds with the 3 kN thrusters, and a fuel consumption of 142.7 kg.
To understand the burn better, and compare with my planning calculations, it is useful to consider a reference frame formed by the following vectors: the unit radial vector \(\widehat{r}\), the unit vector \(\widehat{v}_u\) that points along the vector \(v_u\) that is the projection of the velocity \(v\) onto the plane orthogonal to \(r\), and the orbit normal \(n = \widehat{r} \times \widehat{v}_u\).
The velocity before the burn in this frame was
[23.303, 95.900, 0].
Note that the first component is the radial velocity \(\|v_r\|\). The delta-V written in this frame was
[-20.501, -83.515, 94.210].
This shows that the burn didn’t happen in the plane orthogonal to \(r\), and in fact most of the radial velocity was cancelled out, thus lowering and advancing in time the apoapsis of the orbit. With the pre-burn orbit, the apoapsis radius was 185153 km, and its time would have been 14:24:17 UTC. With the post-burn orbit, the apoapsis radius is 184930 km, and apoapsis passage was at 09:39:51 UTC, shortly after the burn.
The components of the delta-V in the \(\widehat{v}_u\) and \(n\) coordinates are quite similar to the VNB coordinates that I computed in my planning.
The angular momentum of the pre-burn orbit was 17735 km²/s, and the angular momentum of the post-burn orbit is 17572 km²/s, so it has been reduced by 1% in order to lower the periapsis altitude to 280 km. The angle between the angular momentum vectors, which I denoted by \(\alpha\) in my previous post, is 82.5 degrees, and the inclination of the new orbit is 87.3 degrees. This is very close to the 86.9 degrees given in the mission plan shown in Wikipedia.
The calculations for this post have been done in this Jupyter notebook and this GMAT script.
280 km seems low. Are they planning aerobraking?
I guess not, since they seem to have plenty of fuel. Wikipedia gives a periapsis of 265 km for all the future orbits of the mission.