Yesterday I published a post explaining how Tianwen-1 is transmitting real time state vectors for its own orbit in its telemetry and how we’ve used those to propagate its orbit and track the spacecraft with the Bochum observatory 20m dish. However, there seemed to be some problem in the way we were interpreting the state vectors, since the ephemerides derived from these had a pointing error of a few degrees when compared with observations from Bochum and other smaller Amateur stations.
As of writing that post, I believe I have found the problem. It has to do with the way that the timestamps from the state vectors are interpreted. After correcting this problem I am getting an orbit that matches the observations well. Here I explain this problem and show some more details about the corrected ephemerides.
Correction of the timestamps
I will write a post in a few days explaining in detail what we have been able to find about the telemetry of Tianwen-1. In the mean time, interested readers can refer to this very nice post by r00t.cz. For the purposes of this post it suffices to say that state vectors are transmitted as 6 double precision floating point numbers plus a timestamp. The timestamp consists of a 32 bit counter. The LSB of this counter corresponds to 100us, but we don’t know the epoch of this counter (i.e., what is the time that corresponds to the value zero of this counter).
By looking at the values of the counter, at first it might seem that the epoch is 2020-07-23 00:00 UTC, which might make sense, because the launch day was 2020-07-23. However, this is not quite true. If we use this epoch we obtain timestamps that are approximately 57 minutes larger than they should, as we know that these and other timestamps in the telemetry should correspond to real time data. So approximately 57 minutes need to be subtracted from the epoch (or from the timestamp).
The main problem with the two sets of state vectors that I considered in my previous post is that set1 had been corrected approximately for this 57 minute offset, while set2 had not, and we didn’t notice it. When I tried to examine the sets of state vectors for self-consistency, set1 seemed to be OK, as indeed it was, but set2 also seemed to be OK. Set1 was from shortly after launch, so a mistake in the timestamp would cause a large effect in the relative positions of Tianwen-1 and Earth (recall that the state vectors use heliocentric coordinates). However set2 was from Saturday morning, so even a large mistake in the timestamp wouldn’t change the orbit so much.
I have tried to determine more precisely the timestamp offset by doing the following experiment. The first state vector we’ve ever decoded from Tianwen-1 is
77370211.41732779 -120040665.5773057 -52035627.25877059 31.626899470825165 15.031561106807159 7.495133460502749
This corresponds to the beginning of a recording made by Paul Marsh M0EYT on 2020-07-23 06:26:51 UTC, so its timestamp must be approximately near this (recall that a real time state vector is transmitted every 32 seconds).
The next short recording that we have by Paul starts at 2020-07-23 06:40:07 UTC, and its last state vector is
77416179.26727146 -120018414.60685001 -52024602.44255043 30.897467608133603 15.171754294969595 7.477456413260109
We don’t know the exact timestamps of these two state vectors, but we do know that there is exactly a difference of 1472.0151 seconds between them, according to their timestamp counters.
Thus, an approximate timestamp is taken for the first state vector, and it is propagated in GMAT for 1472.0151 seconds. The position error with respect to the second state vector is computed. Then we search for the timestamp that when assigned to the first state vector minimizes this position error. The GMAT script used to do this can be found here.
It turns out that the best timestamp for the first state vector is 2020-07-23 06:40:24.1815 UTC, which corresponds to subtracting 3400.2 seconds to the 2020-07-23 00:00 UTC timestamp. I have used a granularity of 0.1 seconds when searching for the best timestamp.
Therefore, my conclusion is that the epoch for on-board timestamps is 2020-07-22 23:03:19.8 UTC. I believe this to be certain within a few seconds of margin, which is enough precision to interpret the state vectors correctly, especially now that Tianwen-1 is further away from Earth.
Comparison of state vectors
With the timestamp correction, the last state vector we collected on Sunday morning is
2020-07-26 10:52:42.492400 85150291.38521843 -115825547.73814942 -50010362.140319996 27.6141067728233 15.896750416323576 7.561247260377793
Recall that this is to be interpreted as heliocentric ICRF coordinates in km and km/s.
Comparing this state vector and the one from 2020-07-23 06:26:51 UTC in this GMAT script we have the orbits shown below.
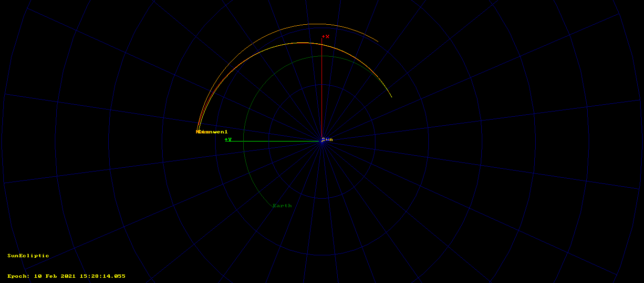
The orbit from 2020-07-23 arrives to within 2.2 million km of Mars on 2021-02-02, while the orbit from 2020-07-26 arrives to within 3.2 million km of Mars on 2020-02-10.
If we propagate the state vector from 2020-07-26 backwards to the epoch of the one from 2020-07-23, we see that the tracks do not coincide, but are more or less close together (compare this with the similar plot in my previous post). Since we don’t fully understand the nature of these on-board state vectors, we don’t know what accounts for the difference. Maybe a correction manoeuvre performed after launch, or the Chinese DSN uploading corrected information that accounted for any small deviations from the nominal launch trajectory.
Comparison with Amateur observations
The figures below show the distance from Earth and right ascension and declination coordinates for the two sets of ephemerides considered in the previous post (recall that set2’s timestamp was wrong by almost one hour), and set3, which comes from the 2020-07-26 10:52:42 UTC state vector.
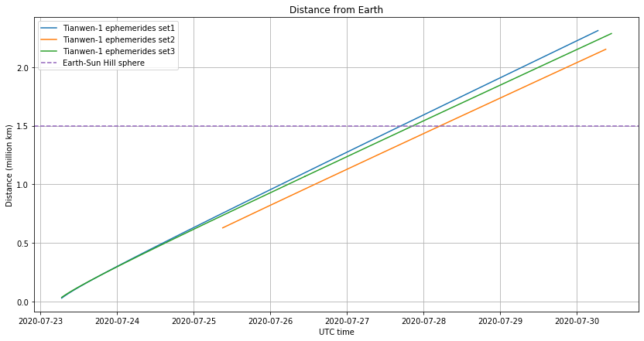
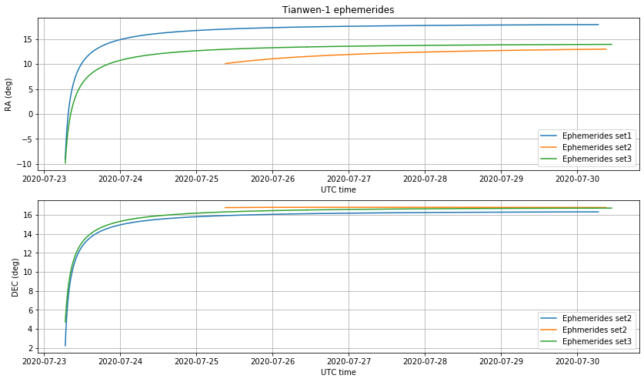
We see that set2 was clearly wrong, and set1 and set3 start quite similar but then diverge, especially in right ascension.
Below we show the comparison of the ephemerides with the antenna pointing from Bochum, which has a beamwidth of 0.1 degrees at X-band. We see that set3 is a good match within a fraction of a degree.
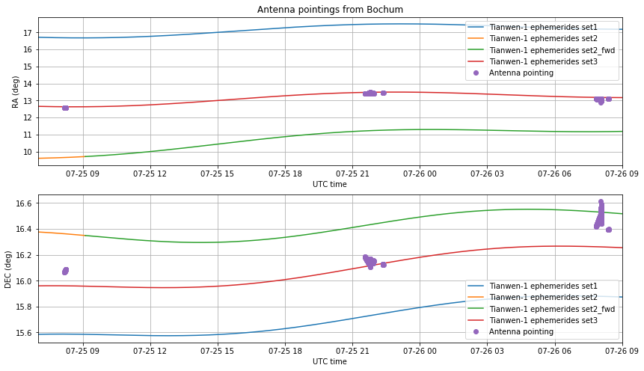
It is also interesting to study the antenna pointing data from Paul’s station, which is not as precise as Bochum but has also data from shortly after launch. Again, set3 is a good match, even for 2020-07-23, where it matches the observations by Paul better than set1, which is what was being downlinked on the telemetry at that moment.
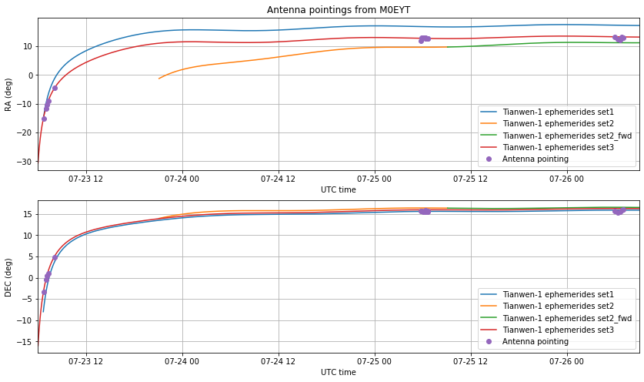
This Jupyter notebook contains the calculations made for the plots above, as well as plots corresponding to three other Amateur stations which also show good match with set3.
Right ascension and declination table
I have made this GMAT script to propagate the state vector from 2020-07-26 10:52:42 UTC (set3 above) all the way to Mars and generate a table of right ascension and declination coordinates, with the help of the radec_convert.py script for formatting. The table is here. Amateur stations report that the table is working well for them during Monday 2020-07-27 and Bochum has used their own propagator and the same state vector to track Tianwen-1 during Monday with no corrections needed to their 0.1 degree beam.
Comparison with ephemerides from optical observations
Project Pluto published yesterday the following pseudo-MPEC for Tianwen-1, which uses data from optical observations to estimate an orbit (thanks to Nico Janssen PA0DLO for pointing me to this resource, which I didn’t know).
I have used this Jupyter notebook to compare the azimuth and declination coordinates from Project Pluto with those in the table given above (the output file from GMAT is used, since it has more resolution that the table). The figure below shows the difference between Project Pluto and the table. This shows good agreement to within a few arcseconds.
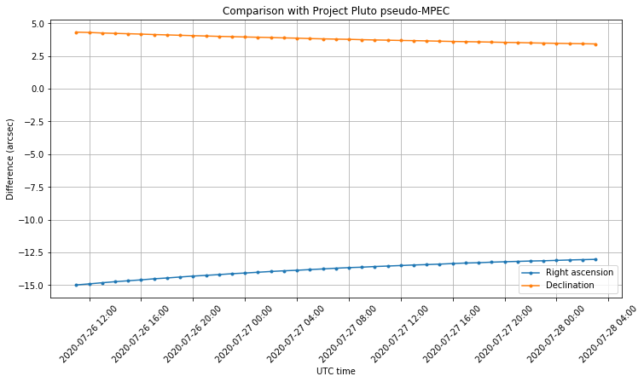
Project Pluto reports a mean residual of 0.254 arcseconds of the orbit fitted to 67 optical observations between 23 and 26 of July. Consider what it means that the error we are finding between the state vectors and Project Pluto ephemerides is only a few arcseconds. At a distance of one million km, one arcsecond corresponds to a displacement of about 5km. The Earth moves at 30km/s along its orbit, so making a mistake of one second in the timestamp of the heliocentric state vectors will change the respective positions of Tianwen-1 and Earth by 30km. Therefore, the error of a few arcseconds seems very good, taking into account that we have estimated the timestamps epoch as indicated above.
It would be interesting to compare also the optical observations themselves with the trajectory propagated from the state vectors, but since this requires considering the locations of all the observers is maybe a topic for a future post.
Extracting state vectors from the telemetry data
I have put up a very crude Python script called extract_state_vectors.py that is able to extract and print out the state vectors from a file containing telemetry frames. Tianwen-1 uses 220 byte AOS Space Data Link frames sent using CCSDS concatenated FEC. Two file formats are supported by the script: one that contains the 220 byte frames concatenated, and another one that contains 256 byte frames composed by the CCSDS 32 bit syncword, the 220 byte frame, and the 32 Reed-Solomon parity check bytes. This script already applies the timestamp correction described in this post.
This script relies on the fact that the layout of the Tianwen-1 telemetry is currently very regular, so it is able to get to the state vectors just by reading a few header fields, without having to parse upper layer protocols. Just by chance, it happens that state vectors are always transmitted on spacecraft ID 245, virtual channel 1, whenever the virtual channel frame count is congruent to 22 modulo 64, and the vectors and timestamp are located at fixed positions within these frames. This is what the script uses, so it could break any moment that the telemetry layout changes.
The correct way to do it is to parse Space Packets and filter using the APID (application ID), which is what r00t.cz is doing. More details about the telemetry will be included in a future post.
5 comments