The Parks-McClellan FIR filter design algorithm is used to design optimal FIR filters according to a minimax criterion: it tries to find the FIR filter with a given number of coefficients whose frequency response minimizes the maximum weighted error with respect to a desired response over a finite set of closed sub-intervals of the frequency domain. It is based on the Remez exchange algorithm, which is an algorithm to find uniform approximations by polynomials using the equioscillation theorem. In signal processing, the Parks-McClellan algorithm is often call Remez. This algorithm is a very popular FIR design algorithm. Compared to the windowing method, which is another commonly used algorithm, it is able to obtain better filters (for instance, meeting design constraints with less coefficients), in part because it allows the designer to control the passband ripple and stopband attenuation independently by means of the weight function.
I have been laying some groundwork for Maia SDR, and for this I will need to run the Parks-McClellan algorithm in maia-httpd, the piece of software that runs in the Pluto ARM CPU. To evaluate what implementation of this algorithm to use, I have first gone to the implementations that I normally use: the SciPy remez function, and GNU Radio’s pm_remez function. I read these implementations, but I didn’t like them much.
The SciPy implementation is a direct C translation of the original Fortran implementation by McClellan, Parks and Rabiner from 1973. This C translation was probably written decades ago and never updated. The code is very hard to read. The GNU Radio implementation looks somewhat better. It is a C implementation that was extracted from Octave and dates from the 90s. The code is much easier to follow, but there are some comments saying “There appear to be some problems with the routine search. See comments therein [search for PAK:]. I haven’t looked closely at the rest of the code—it may also have some problems.” that have seemingly been left unattended.
Because of this and since I want to keep all the Maia SDR software under permissive open source licenses (the GNU Radio / Octave implementation is GPL), I decided to write from scratch an implementation of the Parks-McClellan algorithm in Rust. The result of this has been the pm-remez crate, which I have released recently. It uses modern coding style and is inspired by recent papers about how to improve the numerical robustness of the Parks-McClellan algorithm. Since I figured that this implementation would also be useful outside of Maia SDR, I have written Python bindings and published a pm-remez Python package. This has a few neat features that SciPy’s remez function doesn’t have. The Python documentation gives a walkthrough of these by showing how to design several types of filters that are commonly used. This documentation is the best place to see what pm-remez is capable of.
The rest of this post has some comments about the implementation and the things I’ve learned while working on this.
One of the things I’ve found when documenting myself is that many sources that explain the Parks-McClellan algorithm don’t go into all the details that are needed to implement it. They leave a taste of understanding a global picture of what the algorithm does, but not how each step works exactly. An example of this kind of explanation is in Section 3.3 in fred harris’ book. A book which does a much better job at explaining the algorithm is Oppenheim and Schafer, in Section 7.7. The GNU Radio implementation mentions some equations and notation from this book, so it is convenient to have it at hand when studying the code.
But by far the best description that I have found of the Parks-McClellan algorithm is in the paper that presents McClellan, Parks and Rabiner original Fortran implementation of the algorithm. The paper includes the Fortran code, but the text of article has all the necessary explanations, equations and flowcharts, so it is not really necessary to try to read the Fortran code. This paper assumes some familiarity with the Parks-McClellan algorithm, so it should be preceded by reading either the original Parks-McClellan paper (which is a good read on its own, although it is more about the mathematics that about algorithmic implementation details), or one of the textbooks mentioned above.
Another nice paper that I have found is A Robust and Scalable Implementation of the Parks-McClellan Algorithm for Designing FIR Filters, by S.I. Filip. This is a paper from 2016 that describes how to improve the Parks-McClellan algorithm to make it work in situations which are prone to numerical ill-conditioning, such as when designing filters with many coefficients, steep transitions or large attenuation factors. The paper is accompanied by a C++ implementation, which can be consulted when some small details are omitted in the paper.
Section 7.2 of the paper is interesting because it benchmarks the implementation described in the paper against SciPy, GNU Radio and MATLAB. A series of example problems are defined, and the runtimes of each implementation and whether it converges or fails are measured. The takeaway from this section is that the GNU Radio implementation is less robust than SciPy and MATLAB, but it is also much faster.
I have taken mainly two ideas from this paper for my pm-remez implementation. The first is Section 5, which analyses the numerical errors of polynomial interpolation and proposes to use barycentric Lagrange interpolation. The second is Section 6, which proposes to use Chebyshev proxy root finding to find the local extrema of the weighted error function. A key step in the Parks-McClellan algorithm is the Remez exchange step. There, the local extrema of the current weighted error function are found, and these extrema are used as polynomial interpolation nodes for the next iteration of the algorithm.
The original Fortran implementation, as well as the SciPy and GNU Radio implementations, evaluate the error function over a finite grid of points to approximate the local extrema. There are better approaches to find the local extrema, such as Chebyshev proxy root finding, a variant of which is also used in the MATLAB implementation of the remez function. In this method, the weighted error function is approximated by a Chebyshev interpolant in a small interval, and the zeros of the derivative of this interpolant are found. If the approximation is good, these zeros are close to the local extrema.
Finding the zeros of this polynomial is usually done by solving an equivalent eigenvalue problem. The C++ implementation by Filip uses the Eigen library, which is a modern C++ template library. This allows Filip’s implementation to use MPFR to do benchmarks/debugging and to solve very ill-conditioned problems which are impossible to solve with double-precision arithmetic. Unfortunately, there isn’t a nice equivalent of Eigen in Rust. The only reasonable way to compute eigenvalues seems to be with the ndarray-linalg crate, which uses LAPACK. This is a bit of a let-down, because it makes my project feel as running away from some old piece of Fortran only to end up depending on another old piece of Fortran. I briefly considered writing an implementation of the QR algorithm from scratch, but doing this properly seemed like a whole project on its own, because LAPACK does a lot of numerical computing tricks to make it work well in practice.
I still have taken Filip’s idea of using a higher-precision floating point implementation to solve tricky problems, so my implementation allows using num-bigfloat, although these floats need to be converted to float64 to compute the eigenvalues, because that’s the only that LAPACK can handle.
Another important point of the Parks-McClellan algorithm that is often not treated in enough detail is that it only serves to design FIR filters with an odd length and even symmetric taps. The frequency response of this type of FIR filters is a polynomial in the cosine of the frequency, which is what allows to turn the filter design problem into a polynomial approximation problem. Nevertheless, the problem of designing other types of FIR filters can be reduced to the case of odd length and even symmetry by scaling the frequency response with a suitable trigonometric function (and as a consequence, scaling the desired function and weight too). The paper by McClellan, Parks and Rabiner explains this very clearly in Section II. It includes the formulas about how to scale the desired function and weight depending on the type of the filter in a flowchart in Figure 2, and formulas to convert the taps of the odd length even symmetry filter designed by the algorithm into the required filter in equations (7)-(12). Regarding this point, it is convenient to mention that the GNU Radio implementation computes the taps by scaling the frequency response of the filter depending on each case, but given that there are straightforward formulas to transform the taps, I don’t see the point in doing this.
According to these conversions, there are four cases in which the algorithm can work. These depend on whether the length is odd or even, and on whether the taps have even or odd symmetry. These cases are sometimes referred to as Type I, Type II, Type III and Type IV FIRs, but I find this nomenclature confusing and never remember which is which. The following Figure from Oppenheim and Schafer is a good reminder.
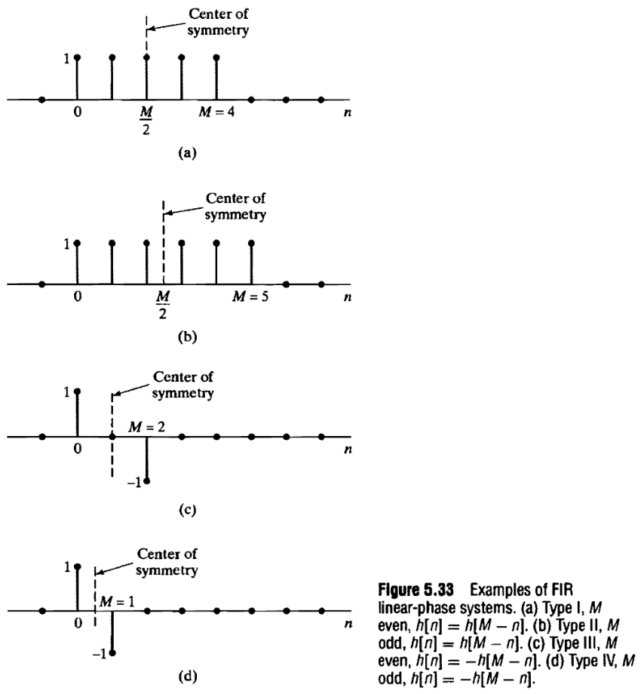
Most filters used in practice have even symmetry (Type I or Type II), but there are special classes of filters that are occasionally required that have odd length and odd symmetry (Type III). These are the Hilbert filter and the differentiator filter. The SciPy and GNU Radio implementations treat the Hilbert and differentiator filters as special cases, making the algorithm less flexible and the code harder to read. In my implementation the user can specify whether the length of the filter is even or odd (indirectly, by specifying the length), and whether the filter taps should have even or odd symmetry. Hilbert and differentiator filters can be designed by setting these parameters appropriately, as shown in the example of the pm-remez Python documentation.
Related to differentiator filters is the ability to set a custom desired response or weight function. The original Fortran implementation has functions EFF and WATE that define the desired frequency response and the weights. The authors say that if the user needs custom functions, they can replace these functions. This made sense for Fortran code in the 70s, but in the present day with modern languages we can let the user pass an arbitrary closure to define a custom function if they need to. This is what I have done in pm-remez. In the Rust API, the desired response and weight function are defined by closures Fn(T) -> T (where T is the scalar type, for instance, T = f64), so the user can pass in whatever custom functions they want and enjoy compile time optimizations. I reckon that most of the time the user needs a constant or linear response in each band, so there are shorthands to set those. The Python API also has the same flexibility. The response in each band can be defined either as a single scalar, indicating a constant response, a pair of scalars, indicating a linear slope, or a Python callable, which is used to define an arbitrary function.
There is nothing specially magical or easier about having a constant desired response and weight in each band. Even designing a lowpass filter with an even number of taps involves non-flat desired response and weight functions, due to the scaling done to transform the problem into one involving a FIR with an odd number of taps. Therefore, not letting the user define these functions arbitrarily is just bad API design in the present day.
Having the capability to define the desired response and weights freely permits to handle some interesting filter design problems. The first is lowpass filters with a 1/f response in the stopband. fred harris advocates for the use of these filters instead of equiripple filters in Section 3.3.1 of his book. He explains that these 1/f filters can be designed by setting the weight function to an increasing linear slope in the stopband. He also comments that some Parks-McClellan implementations don’t allow this, in which case a staircase weight function realized by defining several adjacent stopbands with increasing constant weights can be used as an approximation. This is one of shortcomings I find with SciPy’s remez function. In contrast, the pm-remez Python API allows to design this kind of FIR almost as easily as an equiripple filter, as shown in the documentation examples.
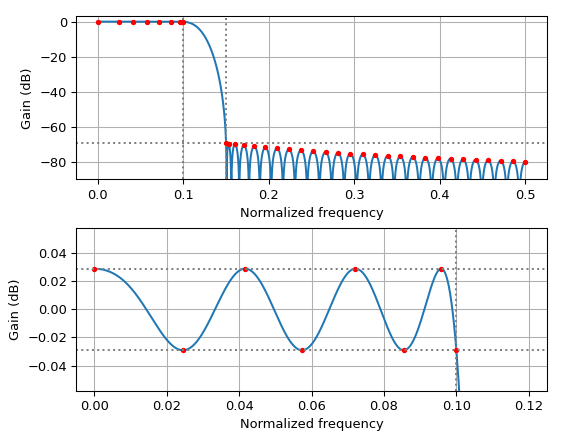
Another FIR filter that requires a linear slope (this time for the desired function) is the differentiator. The SciPy and GNU Radio implementations handle this by treating the differentiator as a special case and overriding its desired function. With pm-remez, designing a differentiator is just treated in the same way as any other filter, by specifying a linear desired response in the passband.
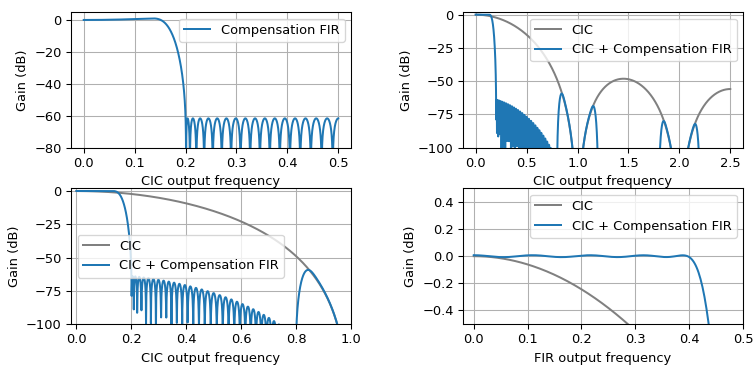
Finally, my favourite example that requires a non-constant desired response is a CIC compensation filter. The passband response of this filter needs to be the inverse of the CIC frequency response, which involves some sine functions. The Python documentation shows how to design a compensation filter that looks like this.
Installing the pm-remez Python package is just a
pip install pm-remez
command away. There are pre-built packages for Linux x86_64, Windows x86_64, and MacOS x86_64 and arm64. I will certainly be using pm-remez for my filter design tasks in the future, instead of SciPy’s remez function.
One comment