Today, 2021-02-05 at 12:00 UTC, Tianwen-1 has executed TCM-4. This is its last trajectory correction manoeuvre before the arrival to Mars orbit next Tuesday February 10. This was reported by Chinese media together with a black and white image of Mars taken recently by the spacecraft.
As usual, I have analysed this manoeuvre by propagating forwards the last state vector that we have from the spacecraft’s telemetry before the manoeuvre, propagating backwards the first state vector that we have after the manoeuvre, and finding the intersection point of the two trajectories.
This time the result is not very precise because of two reasons. First, the last state vector we have from before the manoeuvre is from 2021-02-02 23:33 UTC due to a problem with the telemetry reception in AMSAT-DL‘s Bochum observatory. Therefore, we need to propagate this state vector 2.5 days forward, whereas in other manoeuvres we had more recent state vectors. Second, this manoeuvre is a small correction, so the angle between the trajectories is small and finding their intersection is an ill conditioned problem.
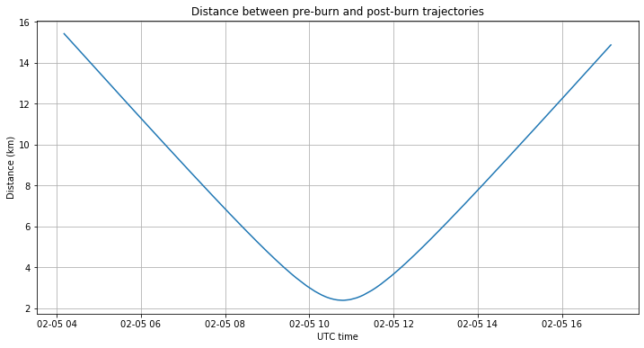
The figure below shows the distance between the pre-burn and post-burn trajectories. The minimum happens at 10:47:51 UTC, which is quite far from the timestamp of 12:00 UTC reported by the media. The minimum distance is 2.4 km. There is no reason to believe that the media is not correct, since in other occasions the minimum was much smaller than 1 km, which already speaks about the bad accuracy of this method.
The delta-V vector in ICRF coordinates and m/s is the following. This should be quite accurate, even thought the time of the burn could not be found precisely.
[ 0.49150875, 0.29430668, -0.28538354]
The magnitude of this vector is 0.64 m/s.
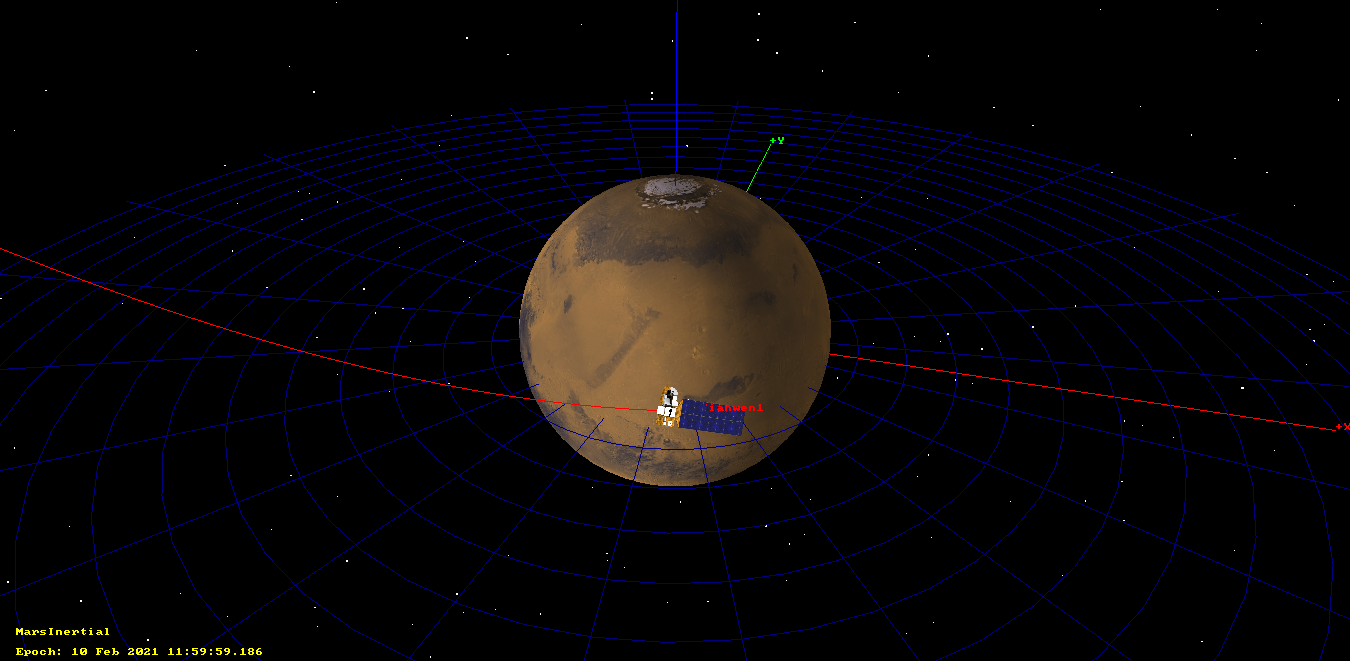
The arrival trajectory can be seen in the figure below, which shows an orbit simulation in GMAT. The periapsis height is 408 km, and the inclination is 10.9 degrees. Note that the periapsis passage is almost exactly at 12:00 UTC. This is perhaps a coincidence, or maybe the result of deliberate and careful orbit planning.
The specific energy of the orbit is 3.10 km²/s², and the periapsis velocity is 5.36 km/s. For a capture orbit with a period of 11 days, as mentioned in this article, the required delta-V is 660 m/s. Assuming a specific impulse of 321.6 s (see this comment) and a thrust of 3 kN (this value has appeared published several times in the media), this delta-V will spend 836 kg of fuel over 879 seconds. Note that the delta-V that would be required for a parabolic orbit insertion (i.e., to obtain a specific energy of zero) is 614 m/s, so the capture into an 11 day orbit is only slightly more expensive. The spacecraft will move later into a parking orbit with a period of around 2 days.
The figure below shows an example capture orbit with a period of 10.69 days. It was obtained by burning retrograde for 889 seconds around periapis. The resulting orbit has a periapsis altitude of 293 km.

The calculations and orbit simulations used in this post can be found in this Jupyter notebook. Best of luck to CNSA with the Mars orbit insertion!
30 comments