Oscillations and relativistic effects in Galileo broadcast clocks

A few days ago, Bert Hubert, the creator of galmon.eu, discovered a sinusoidal oscillation in the clock drift \(a_{f1}\) parameter of the broadcast ephemerides of Galileo satellites. This variation has a frequency that matches the orbital period of 14 hours and 7 minutes. At first, I suggested that it might be caused by relativistic effects, which are given by\[-\frac{\sqrt{\mu}}{c^2}e\sqrt{A}\sin E,\]where \(\mu\) is the Earth’s gravitational parameter, \(c\) is the speed of light, \(e\) is the eccentricity, \(A\) is the semi-major axis, and \(E\) is the eccentric anomaly. In fact, the order of magnitude of the oscillations that Bert was seeing seemed to agree with this formula.

However, then I realised that this relativistic effect is not included in the broadcast clock model. It needs to be included back by the receivers. Therefore, it shouldn’t appear at all in the broadcast clock. Something didn’t seem quite right. This post is an in-depth look at this problem.

First we start by reviewing the relevant theory about relativistic effects in GNSS satellite clocks. The article “Relativity in the Global Positioning System” gives a good overview of relativistic effects affecting GNSS systems. In equation (39) it proves the formula given above for the relativistic effect on the satellite clock due to a non-circular orbit.

When GNSS clocks are modelled, it is common to correct for this effect in the clock observations, so as to remove the effect from the clock model. Doing so has the advantage that this relatively large periodic term is eliminated from the clock model, simplifying clock modelling and analysis. However, the GNSS receiver needs to put back the correction in order to compute the satellite clock correctly.

Regarding the major constellations, GPS, Galileo and BeiDou remove relativistic effects from their broadcast clock models. This is described in Section 20.3.3.3.3.1 of IS-GPS-200K, in Section 5.1.4 of the Galileo OS SIS ICD v1.3, in Section 5.2.4.9 of the BeiDou B1I SIS ICD v.3.0 and in other related BeiDou documents, and in equation (E.4.16) in the RTKLIB manual. In contrast, GLONASS doesn’t remove the relativistic effects from its broadcast clock model.

When performing orbit and clock determination for the production of precise orbit and clock products, such as those listed in the IGS MGEX, the common practice is to remove the relativistic effect from the clock model. Therefore, the relativistic correction needs to be added again when using an SP3 file. More information can be found in equation (E.4.37) in the RTKLIB manual.

Therefore, when studying broadcast clocks or SP3 precise clocks, we expect not to find this relativistic effect, except when dealing with GLONASS broadcast clocks.

In the experiment presented in this post we look at oscillations in the broadcast and SP3 clocks of satellites of all the major constellations with the goal of studying oscillations at a frequency of 1/revolution. The set of data under study is the MGEX BRDC files for the complete month of November 2019, and the final SP3 clocks from CODE ranging between 2019-11-01 and 2019-11-23 (since final products for the last week in November are not available yet).

In order to simplify the experiment, we study a single satellite per constellation. To magnify the effects due to a non-circular orbit, we choose the satellite having the largest eccentricity. For GPS, that satellite is G21, but because of some anomalies explained below, we chose instead G02, the satellite having the second largest eccentricity. For Galileo, we ignore the highly eccentric satellites E14 and E18, due to the difficulties of modelling their orbit accurately. We choose E31, which has the highest eccentricity among the operational satellites. For BeiDou, the satellites having the largest eccentricity are in an IGSO orbit. Due to the radical differences between an IGSO and a MEO orbit, we choose an IGSO and a MEO BeiDou satellite. The IGSO having the largest eccentricity is C06, while the MEO having the largest eccentricity is C11. For GLONASS we choose R16, which has the largest eccentricity.

The amplitude of the relativistic effect in the satellite clock bias for these satellites is as follows:

• E31, 0.958 ns
• G02, 44.4 ns
• C06 (IGSO), 24.1 ns
• C11 (MEO), 5.30 ns
• R16, 6.10 ns

The effect in the satellite clock drift is:

• E31, 0.119 ps/s
• G02, 6.47 ps/s
• C06 (IGSO), 1.76 ps/s
• C11 (MEO), 0.717 ps/s

Since the GLONASS broadcast ephemerides don’t include the clock drift parameter, the clock drift of R16 will not be studied.

First we look at the clock drift \(a_{f1}\) parameter in the broadcast ephemeris during November. The figure below shows the clock drift for E31 and G02. The average of each trace has been removed to aid visualization.

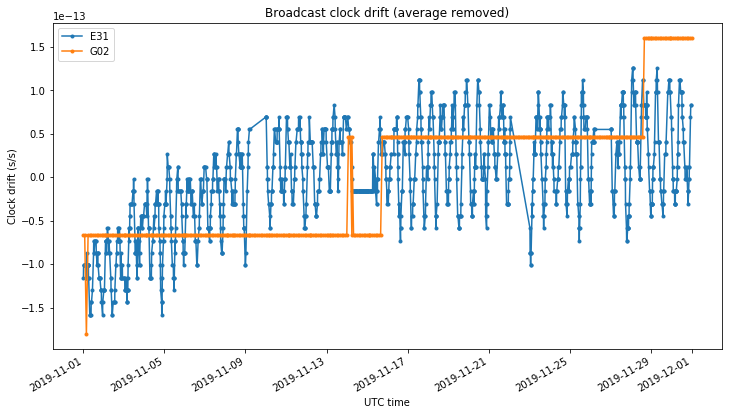
We clearly see the oscillatory behaviour that Bert first noticed in the Galileo broadcast ephemeris. In contrast, the broadcast clock model for GPS is very simple. The \(a_{f1}\) term is constant except for some jumps every several days.

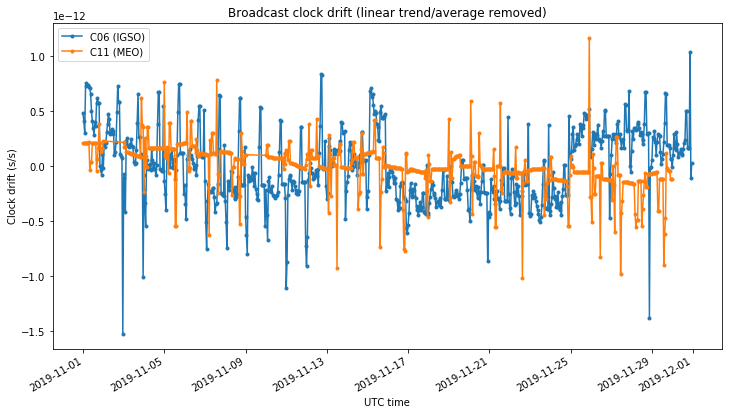
Next we show the clock drift for the BeiDou satellites. The IGSO C06 has a strong linear trend that has been removed in the plot. We see some large spikes in some of the ephemerides, but no oscillatory behaviour is visible.

Now we examine the clock bias \(a_{f0}\) parameter in the broadcast ephemerides. We fit and remove a degree 4 polynomial to the data when plotting in order to eliminate long term drift. The figure below shows the clock bias for E31 and G02.

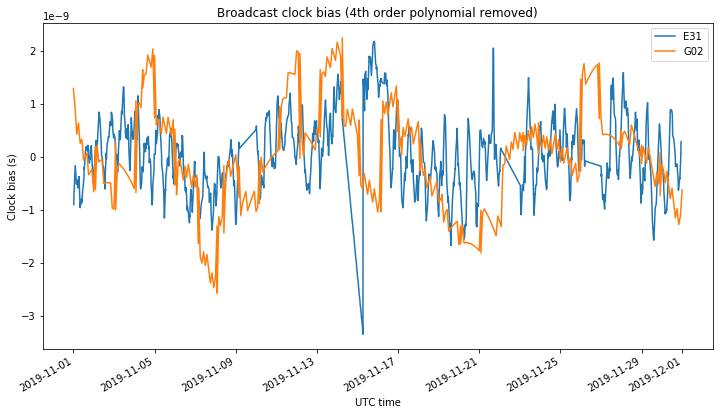
The clock bias of E31 shows the same oscillatory behaviour as the clock drift (but there are other effects, making the graph more noisy). G02 doesn’t show this oscillatory behaviour but shows some noticeable jumps every other day.

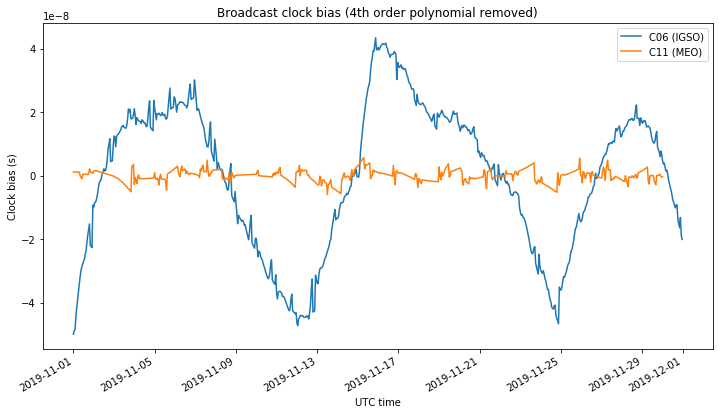
The figure below shows the clock bias of the BeiDou satellites. The IGSO C06 has a really large and complex long term drift pattern that is difficult to cancel by fitting a low degree polynomial. The interpretation of this plot is therefore not easy.

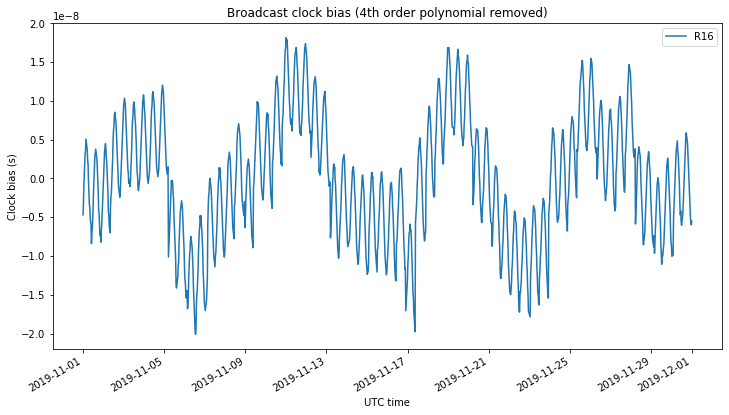
Finally, we show the clock bias of the GLONASS satellite R16. Besides a slow variation, the relativistic effect (which is included in the broadcast clock model) can be clearly seen in the graph.

Now we perform a spectral study of the \(a_{f1}\) and \(a_{f0}\) parameters in order to see more easily the oscillations occurring at different frequencies. The figure below shows the spectrum of the clock drift for E31 and G02. The horizontal axis has been normalized to units of 1/revolution (which are different for each constellation, due to different orbital radii).

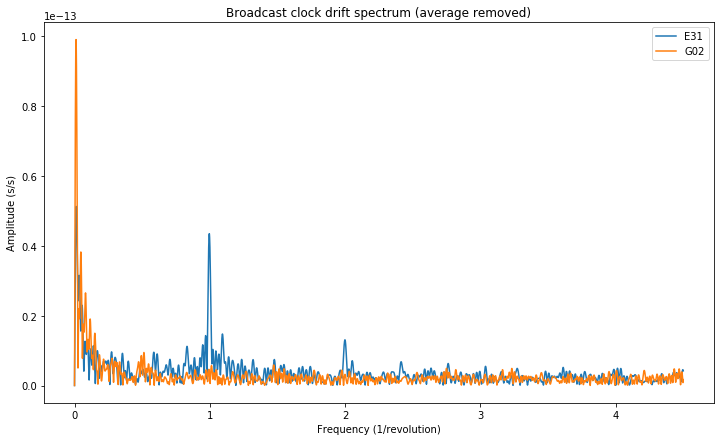
The oscillatory behaviour that we saw in the time domain for E31 is now clearly seen at a frequency of 1/revolution, with an amplitude of approximately 0.05 ps/s. Note that this is roughly half of the relativistic effect computed above, but I don’t know if this is just a coincidence or if it is significant. A harmonic at a frequency of 2/revolution can also be seen. In contrast, the spectrum of the G02 clock drift doesn’t show any features at integer multiples of 1/revolution.

At this moment it is convenient to remark the effects of unmodelled orbital behaviour in the satellite clock determination. Since unmodelled orbital effects will contaminate the clock determination and these unmodelled orbital effects often happen at frequencies which are integer multiples of 1/revolution, spectral features of the clock model can point to defects in orbit modelling.

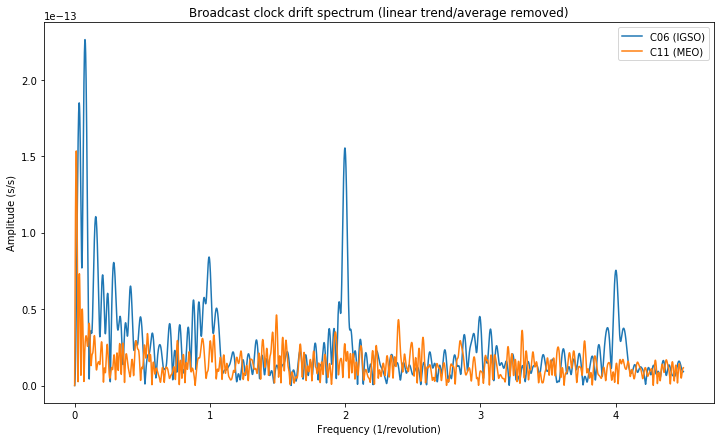
Next we study the clock drift of the BeiDou satellites. We see that the MEO C11 doesn’t display any interesting spectral features, while the IGSO C06 has some features at integer multiples of 1/revolution. Probably these are caused by unmodelled orbital effects as remarked above. In contrast to the case of E31, the harmonic at 2/revolution is stronger than the fundamental at 1/revolution.

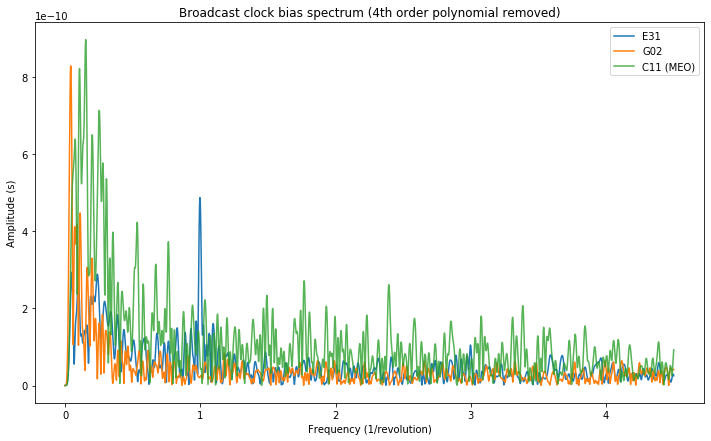
Below we show the spectrum of the clock bias \(a_{f0}\) parameter of E31, G02 and C11. The spectrum of the IGSO C06 is not shown because it is completely swamped by the slow drift. Here it is clearly visible that E31 is the only satellite which presents oscillations at a frequency of 1/revolution. The amplitude of these oscillations is approximately 0.5 ns, which is roughly half the relativistic effect computed above. Again, I don’t know if this is a coincidence.

Now we compare the broadcast clocks with the SP3 precise clocks for each of the satellites. The figure below shows the comparison for E31. While the broadcast clock has a strong component at 1/revolution, the SP3 clock has only a weak component at this frequency that can be explained by clock contamination from unmodelled orbital effects. This seems to indicate that the broadcast clock for E31 is wrong: the oscillatory effect that is clearly visible in the broadcast clock is not a real effect of the satellite clock, but rather a problem when computing the broadcast orbit and clocks.

Additionally, we remark that the SP3 clock looks less noisy. This is often the case for precise clocks in comparison to broadcast clocks (and also the 5 minute sampling interval of the SP3 files as opposed to the longer sampling interval of broadcast ephemerides helps average noise out). Because of this, a weak component at 2/revolution is visible in the SP3 clock. Again, this is probably clock contamination.

The figure below shows the comparison for G02. We don’t see any major spectral features. Something small (probably clock contamination) is visible at 2/revolution.

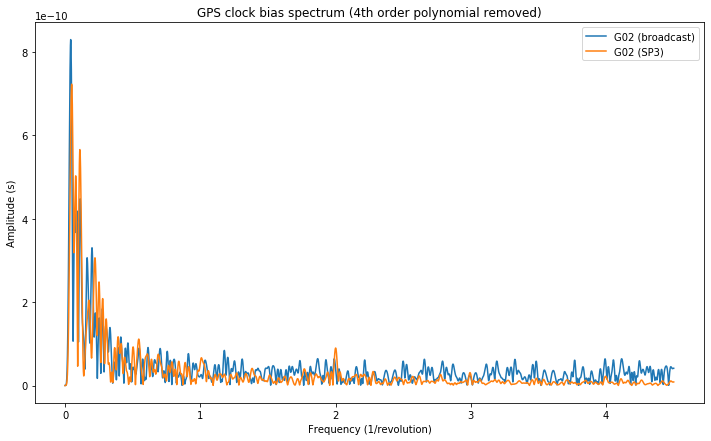
The next figure corresponds to G21 and shows why we have avoided considering this satellite. There are large frequency components in the SP3 file at 1/revolution and 2/revolution that are not present in the broadcast clock. Probably these indicate a problem with the orbit and clock solution that generated the CODE SP3 file. I have decided to discard this satellite rather than investigating this problem further and checking if this effect is also present in the clock solutions computed by other centres.

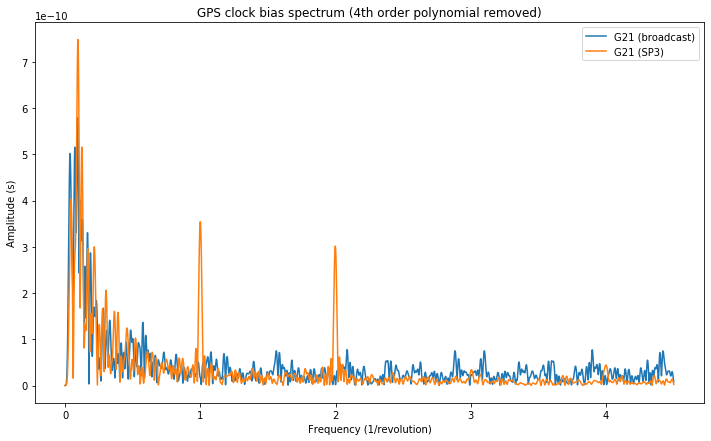
The clock for the BeiDou MEO C11 doesn’t show any major spectral features, as it can be seen in the figure below.

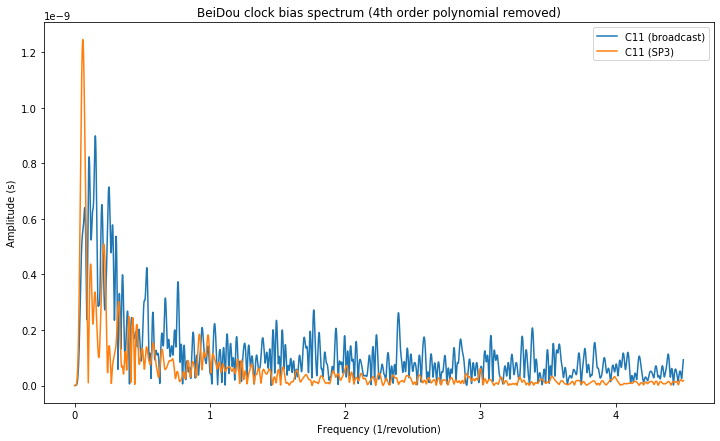
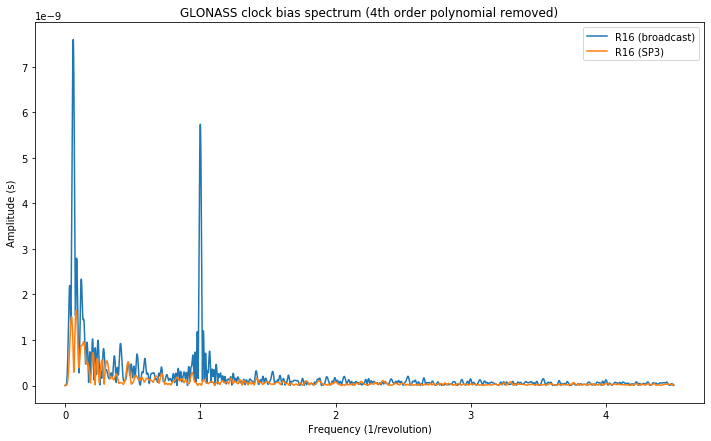
Finally, we show the clock bias spectrum for the GLONASS satellite R16. The large component at 1/frequency that appears in the broadcast clock doesn’t appear in the SP3 clock. This component corresponds to the relativistic effect, which is included in the broadcast clock but not in the SP3 clock. Its amplitude approximately matches the value of 6.1 ns that we had calculated above.

In summary, this post shows that there is something wrong with the Galileo broadcast clock modelling. The coefficients \(a_{f0}\) and \(a_{f1}\) show some oscillatory behaviour at a frequency of 1/revolution which doesn’t appear in the SP3 precise clocks. While this post only studied the satellite E31, Bert Hubert has observed this effect in other satellites as well. The amplitude of these oscillations is in the same order of magnitude as the relativistic correction of the satellite clock due to a non-circular orbit, but it isn’t equal. The comparison with GPS and BeiDou indicates that this is a problem specific to Galileo.

So far I don’t know anything about the cause of this problem. It might be caused by an incorrect relativistic correction of the observations when performing the orbit and clock determination, to clock contamination due to unmodelled orbital effects (but interestingly nothing seems to show up at harmonics of 1/revolution), or to anything else.

The computations and plots in this post have been made in this Jupyter notebook.