ESEO is an educational satellite project for university students led by ESA. It is a microsatellite based on the S-50 platform by SITAEL and indeed serves as an in-orbit validation of that platform. It carries payloads developed by students in 10 European universities, and also a FUNcube payload from AMSAT-UK. It was launched last Monday in the SSO-A launch.
The satellite transmits 9k6 GFSK telemetry in the 70cm Amateur satellite band (do not confuse this telemetry with the telemetry sent by the FUNcube payload in the 2m Amateur satellite band). Last week I wrote an open letter to the directors of the ESEO program requesting the publication of the complete specifications for this telemetry. The existing documentation is published here as two documents called attachment 1, which describes the coding of the frames, and attachment 2, which describes the structure of the telemetry frames.
The main problem motivating my open letter was that the information in attachment 2 was insufficient to produce a telemetry decoder for ESEO. However, last Tuesday an updated version of this document was published. This new version seems to include all the information we need. Apparently, this new version has been published due to my open letter and the pressure made by some people at ESA surrounding the ESEO project.
I would like to thank all the people that have expressed their opinion about the importance of having well documented protocols in the Amateur radio service, as well as all the people in ESA that have pushed for the publication of the documentation, and understood that this is an important matter.
In this post we look at the coding used by ESEO, that is, everything described in attachment 1, and how the decoder in gr-satellites is implemented.
From a quick look at the attachment 1 and the IARU frequency coordination sheet, it seems that the coding is standard AX.25 (perhaps with some form of Reed-Solomon added in the payload), and that is what I expected. However, this is far from the truth. The coding used by ESEO is vaguely reminiscent of AX.25, in that it contains the same ingredients. However, the way that they are integrated together is awkward and the description in attachment 1 is not clear and misses a few important steps.
Luckily, we have been in contact with SITAEL, who have helped us with some examples, and after some work and some trial and error we have been able to figure out the complete details of the coding. Here I will describe the coding from the point of view of the decoder. The encoder goes through the same steps backwards.
As we look at the bitstream of the FSK demodulator output, frames are marked by 0x7e7e flags at the beginning and end of the frame. It seems (and it is logical in view of what will come next) that a frame is always composed of an integer number of bytes between the 0x7e7eflags.
Now, this is reminiscent of the 0x7eflags used by HDLC or AX.25 to mark the beginning and end of each frame. However, in standard AX.25, before getting to the 0x7e flags we need to perform NRZ-I decoding and perhaps G3RUH descrambling on the FSK demodulator output.
After extracting a frame between 0x7e7e flags, we need to reverse the order of each of the bytes (so the least-significant bit becomes the most-significant bit and so on). Equivalently, we can think that bytes are transmitted least-significant bit first, which is also done in standard AX.25. This is an important step, but I have seen no mention of bit ordering in the attachment 1.
After reversing the bytes, we obtain a Reed-Solomon codeword. The details of the Reed-Solomon code are given in attachment 1. It is a systematic (255, 239) code over \(GF(2^8)\). The roots of the generator polynomial for the code are \(\alpha,\alpha^2,\ldots,\alpha^{16}\), where \(\alpha\) is a root of \(p(x) = x^8 + x^4 + x^3 + x^2 + 1\) in \(GF(2^8)\).
Once we have decoded the Reed-Solomon codeword, we need to do some steps which are reminiscent of HDLC, but that actually only make some sense for a continuous stream, and not for a bounded frame as we have here. Thus, the implementation is awkward and not well described in attachment 1.
First, we have to perform bit de-stuffing. Recall that in an HDLC transmitter, every time we have more than 5 consecutive ones, an extra zero needs to be inserted (a process called bit stuffing), to prevent long runs of ones. This extra zero is then removed in the receiver in a process called de-stuffing. Bit stuffing has two goals. First, it prevents a 0x7e from appearing inside the data of a frame. Second, it prevents long runs of ones, which in NRZ-I encoding correspond to a constant value, without bit transitions. A long run of ones would make the receiver lose track of the transmitter’s bit clock. Note that however, long runs of zeros in HDLC are allowed, because a run of zeros in NRZ-I corresponds to an alternating signal that transitions at every bit. Also note that in an HDLC transmitter, bit stuffing is done before NRZ-I encoding (otherwise this reasoning about long runs of ones wouldn’t make sense).
In contrast, in the ESEO transmitter, bit stuffing is done after NRZ-I encoding. Thus, the goal of ensuring enough bit transitions in the signal is not fulfilled by this scheme. A long run of ones may be mapped to a run of zeros by the NRZ-I encoder (depending on the state of the differential encoder). Then, the bit stuffer would let this long run of zeros pass unmodified, resulting in a signal with no transitions.
Also, the condition that no 0x7eflags appear in the data is only fulfilled partially. Since the Reed-Solomon parity check bytes are not bit stuffed, a 0x7ecan appear inside them. It is unlikely but possible that a 0x7e7eflag appears inside the Reed-Solomon parity check bytes, and this could be mistaken as the flag marking the end of the packet. This is a weakness in ESEO’s coding that makes implementing a reliable decoder a bit tricky. Here we have decided to ignore this possibility: in the unlikely event that 0x7e7e appears inside the Reed-Solomon data, the decoder takes it mistakenly as the end of the packet, and so decoding fails.
After de-stuffing, the number of bits in the frame is potentially reduced. However, the frames transmitted by ESEO have an integer number of bytes. Also note that in the transmitter, after bit stuffing, the frame must be padded to an integer number of bytes before doing Reed-Solomon encoding. This padding is simply thrown away in the receiver, so as to get an integer number of bytes after de-stuffing. This is not made clear by the attachment 1.
Once the frame is de-stuffed, we have to perform some form of G3RUH descrambling. Here I use the words “some form” because the G3RUH scrambler is an asynchronous scrambler designed to run on a continuous stream of bits. Here we have a frame, so we need to set up some “boundary conditions” for the descrambler. These are not explained in the attachment 1.
Recall that a G3RUH descrambler works by holding the last 17 received bits in a shift register and XORing the incoming bit with the bits in positions 12 and 17 of the shift register. This may be seen in this diagram. If we want to apply this descrambler to a frame instead of a continuous stream, we need to define the inital value of the shift register at the beginning of the frame. For ESEO this is all zeros (although this is not mentioned in the documentation). Note that this has the inconvenient side-effect that, in the transmitter, a sequence of all zeros is unmodified by the scrambler, since the scrambler shift register is also initialized to all zeros. For this reason, in the usual G3RUH scrambler implementations the shift register is initialized to all ones (although this value is not critical and need not be shared by transmitter and receiver, because the descrambler is self-synchronizing).
After descrambling, we perform NRZ-I decoding. Note that this is backwards from the standard AX.25, where NRZ-I decoding is the first thing that is done to the bitstream. Now, NRZ-I i also designed to be used in a continuous stream of data. Since we are using it on a frame, we need to define the initial condition for the differential decoder at the start of the frame. For ESEO, this is defined as the state zero, but this is not mentioned in the attachment 1.
Once we have performed NRZ-I decoding, the bit ordering of each byte needs to be inverted again. It is not clear why this is done, and there is no mention in the documentation.
Finally, we obtain a packet with the CRC-16 at the end. The CRC-16 algorithm used is specified as CRC-16-CCITT in the attachment 1. CRC-16-CCITT is also used in AX.25, but the algorithm is different from the algorithm used in ESEO. Technically, CCITT only refers to the choice of the CRC polynomial, but there are other parameters needed to specify a CRC algorithm completely: the bit ordering of the input and output bytes, the initial register value, and the final XOR value. These are not mentioned in the attachment 1. The only hint at the correct CRC algorithm is the statement that the CRC of the ASCII string “123456789” is 0x31C3. This helps us find that the correct algorithm is CRC_16_CCITT_ZERO (in the notation of this online calculator), rather than the CRC_16_X25 used in AX.25. These two algorithms only share the polynomial, and differ in all the other parameters.
These are all the details needed to decode the frames of ESEO. After taking all these steps, the frames are indeed AX.25 frames, and the payload should conform to the description of the attachment 2, although I haven’t checked this yet. As some important details I have explained here are not explained in the documentation, and as the deviations from the AX.25 standard are counter-intuitive, obtaining a precise description of the coding has required a fair amount trial and error.
The implementation of the decoder in gr-satellites follows the steps mentioned above. The decoder is shown in the figure below.
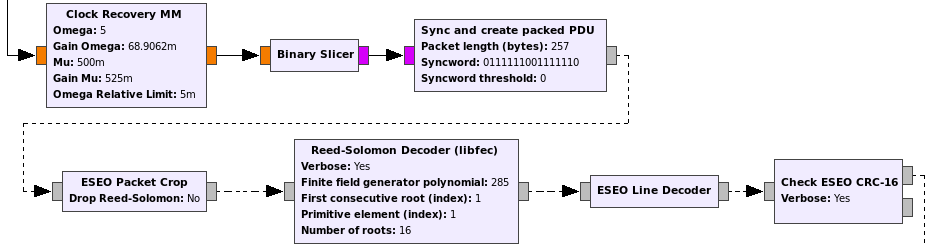
The FM-demodulated stream comes from the top. The clock is recovered, bits are sliced and the Sync and created packed PDU block is used to detect the 0x7e7e flag and create a PDU with the 257 bytes following it. This gives room for the largest packet and its ending 0x7e7e flag, since the size of a Reed-Solomon codeword is 255 bytes.
The ESEO Packet Crop searches the PDU for the 0x7e7e flag marking the end of the data and uses it to crop the packet to the correct length. As remarked above, this block assumes that the sequence 0x7e7e doesn’t occur inside the Reed-Solomon parity check bytes. It also performs byte ordering reversal. Optionally it can drop the Reed-Solomon parity check bytes in case Reed-Solomon decoding is not going to be done. The reason for this feature is that the details of the Reed-Solomon decoder were only figured out at the end, after the rest of the decoder had been implemented.
The Reed-Solomon decoder is based on the decode_rs_char() function of Phil Karn’s libfec, which offers a generic Reed-Solomon decoder. The ESEO Line Decoder block performs de-stuffing, descrambling, NRZ-I decoding and byte reversal as detailed above. Its output is an AX.25 frame with the CRC-16 attached at the end. The Check ESEO CRC-16 block checks and removes the CRC.
The ESEO decoder is now available in gr-satellites in apps/eseo.grc, as well as a sample recording eseo.wav in satellite-recordings. It has been tested with some recordings from the SatNOGS network alsoe, but for these it is convenient to set the Multiply Const block in the decoder to 1 instead of 10, as it seems that they have too much gain. Another pitfall when decoding can be the presence of DC bias in the signal, due to a frequency offset when receiving the signal.
I would like to thank all the people that have worked to make this decoder possible: Mike Rupprecht DK3WN and Ferruccio IW1DTU, who have contributed with recordings, Chris Bridges M0IEB, who has given us valuable data and has been in contact with SITAEL, and Diego Hurtado de Mendoza, who has figured out the details about the CRC-16 and the Reed-Solomon code. Many man-hours would have been saved by having clearly written documentation. For a recent example of a beautifully documented satellite project, see PW-Sat2.
Great work Daniel. To sort out this non standard ax25 in just a few days is an amazing achievement. I hope others will now publish complete details before launch…….perhaps a new IARU requirement? 73
This is amazing detective work and thank you and all your collaborators for this great achievment. It is a great example of the wonderful skills and talent that we have in our midst.
Fantastic work! Well done to all involved.
Most excellent job by all involved! Thanks for helping keep the amateur bands open source!
Daniel,
are there any more decodable wav file from ESEO? It is working with the sample eseo.wav in your github repo.
I recorded some, but I dont able to decode. (more details I sent you is a pm)
t.janos
Hi Janos,
I have been able to decode some recordings from SatNOGS, though I haven’t tried many. Usual problems when decoding are that either the gain is too high/low (modify the gain of the “multiply const block” to fix) or that there is a DC offset in the signal (a DC block can help).
Also, Mike DK3WN managed to decode a few packets.
There are some wav files recorded by HDSDR downloadable from our ES5TO GS:
http://gs1.to.ee/public_to117/p_DSN/ESEO/
Most of the files are cropped so they contain mostly one ESEO beacon.
Viljo, many thanks to make public your good quality recorded files from ESEO on 437 MHz.
I downloaded only 6 and I was able to decode data from 4 of it.
Best wishes,
73
t.janos (from Budapest)
Hi Daniel,
congratulations for the impressive reverse engineering work performed by all the team!
I suppose the “non-standard” choices are involuntary and not directed to obscure the content.
Thanks again for your effort, I’ll try your decoder in GNUradio.
Hi Daniel,
I’m writing a script for decoding multiple wav observation file.
I put a “wav source file” block at the beginning of your flowgraph, in place of udp stream. It works, but your decoder doesn’t quit at the end of wav file. It stays open until Ctr-C. It seems that some gnuradio block doesn’t end its work. This makes my script unuseful, because it hangs on the first wav file.
Any idea to fix it?
Thanks in advance,
Alfredo IZ7BOJ
Hi Alfredo,
I’ve sometimes seen that problem and I don’t know what’s the cause. I suggest you use the gr_satellites command line tool from the gr-satellites next branch. This works fine for decoding wav files (it finishes at the end of the wav file). Though it hasn’t been released officially, the functionality is mostly finished. There is some documentation but it is still in progress.