Following a discussion with Carlos Cabezas EB4FBZ over on the Spanish telegram group Radiofrikis about using Codec2 with DMR, I set out to study the error correction used in DMR, since it quickly caught my eye as something rather interesting. As some may know, I’m not a fan of using DMR for Amateur Radio, so I don’t know much about its technical details. On the other hand, Carlos knows a lot about DMR, so I’ve learned much with this discussion.
In principle, DMR is codec agnostic, but all the existing implementations use a 2450bps AMBE codec. The details of the encoding and FEC are taken directly from the P25 Half Rate Vocoder specification, which encodes a 2450bps MBE stream as a 3600bps stream. Here I look at some interesting details regarding the FEC in this specification.
The FEC works on a frame by frame basis. It takes a 49 bit vocoder frame and encodes it using 72 bits. The following figure, taken from the specifications, summarises the encoding of the frame.
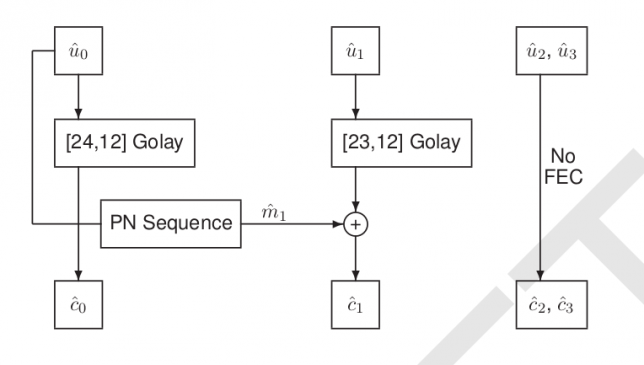
The 49 bit frame is split into four vectors: \(\hat{u}_0\) and \(\hat{u}_1\), both of length 12, \(\hat{u}_2\), of length 11, and \(\hat{u}_3\), of length 14 (see Tables 5 to 8 in the specification for the details). Since each bit in the 49 bit vocoder frame plays a different role, a bit error can be more or less noticeable when decoding the frame depending on which bit it affects. Therefore, some more critical vocoder bits receive more FEC protection than others.
The bits in \(\hat{u}_2\) and \(\hat{u}_3\) are not very critical and are sent uncoded, so here we only concern ourselves with \(\hat{u}_0\) and \(\hat{u}_1\), which are encoded using Golay codes capable of correcting up to 3 bit errors in each of these vectors. The interesting aspect about this FEC is the PN sequence \(\hat{m}_1\) which is used when encoding \(\hat{u}_1\). At the end of Section 5.3, the specification explains that this is done to detect uncorrectable bit errors in \(\hat{u}_0\).
Here the design motivation that we should have in mind is that \(\hat{u}_0\) contains the most critical vocoder bits and that if we are not able to decode \(\hat{u}_0\) correctly, we would like to detect this situation to replace the corrupted vocoder frame by the previous frame or a silent frame, since this is less annoying to the user than playing back the corrupted frame. However, as we will see, the Golay(24,12) code used to encode \(\hat{u}_0\) makes detecting uncorrectable errors a bit difficult.
Geometrically, a Golay(24,12) code is a 12-dimensional linear subspace of \(GF(2)^{24}\) with the property that the closed balls of Hamming radius 3 centred in each element of the subspace are disjoint (and the balls of radius 4 cover all \(GF(2)^{24}\)). Note that each of these balls of radius 3 has\[\sum_{j=0}^3\binom{24}{j} = 2325\]points from \(GF(2)^{24}\). The decoding procedure corrects the points in each of these balls by taking the centre of the corresponding ball. So the decoding succeeds when the codeword lies in any of these balls, but it is correct only when it lies in the same ball as the transmitted codeword (i.e., when there are 3 bit errors or less).
These balls of radius 3 do not cover the whole \(GF(2)^{24}\). In fact, they only contain 9523200 points, so only \(2325/4096 \approx 0.56\) of the whole space is covered. For the remaining points in the space, the decoding procedure fails.
We see that if the bit error rate is high, then the probability that decoding is successful but an incorrect codeword is produce is rather high. In fact, for the extreme case when the bit error rate is 0.5, then the received codeword is a random point in \(GF(2)^{24}\), with uniform distribution. In this case there is a probability of 0.432 that decoding fails, a probability of 0.567 that decoding succeeds but gives a wrong codeword, and a probability of 0.000139 that decoding succeeds and gives the correct codeword. As a rule of thumb, we can think that for high bit error rates, around 50% of the vectors \(\hat{u}_0\) have uncorrectable and undetected errors.
The usual procedure to get around this situation would be to include some form of checksumming into \(\hat{u}_0\). However, this spends extra bits. The solution used by the P25 vocoder FEC is quite interesting, since it doesn’t use any extra bits for checksumming, but rather uses the decoding of \(\hat{u}_1\) as an indicator.
The pseudorandom vector \(\hat{m}_1\) is computed using \(\hat{u}_0\) as a seed. The way that \(\hat{m}_1\) enters the decoding procedure is the one that we can naively think. We receive \(\tilde{c}_0\), which equals \(\hat{c}_0\) plus some bit errors. We decode \(\tilde{c}_0\) to produce \(\tilde{u}_0\) (this may fail, in which case we already have detected uncorrectable errors in \(\hat{u}_0\)). Then \(\tilde{m}_1\) is computed from \(\tilde{u}_0\). We take the received word \(\tilde{c}_1\), add \(\tilde{m}_1\), and then perform Golay(23,12) decoding to obtain \(\tilde{u}_1\).
There are two cases here. If we have correctly decoded \(\hat{u}_0\), so that \(\tilde{u}_0 = \hat{u}_0\), then \(\tilde{m}_1 = \hat{m}_1\), so the input to the Golay(23,12) decoder is the codeword obtained from \(\hat{u}_1\) plus any bit errors that happened in \(\tilde{c}_1\). On the other hand, if we have decoded \(\hat{u}_0\) incorrectly, then \(\tilde{m}_1\) not only does not equal \(\hat{m}_1\), but it looks like a random point in \(GF(2)^{23}\) (with uniform distribution). Therefore the input to the Golay(23,12) decoder also looks like a random point in \(GF(2)^{23}\). Now we look geometrically to Golay(23,12) codes as we have done before for Golay(24,12).
A Golay(23,12) code is a 12-dimensional linear subspace of \(GF(2)^{23}\) such that the closed balls of Hamming radius 3 centred in each point of the subspace are disjoint and cover all \(GF(2)^{23}\). Note that the combinatorics add up, since each of these \(2^{12}\) balls has\[\sum_{j=0}^3 \binom{23}{j} = 2^{11}\]points. The decoding procedure takes a point in \(GF(2)^{23}\) and outputs the centre of the ball in which it lies. Therefore, decoding of a Golay(23,12) code always succeeds.
We are interested in how Golay(23,12) decoding of a random point in \(GF(2)^{23}\) works. The number of errors “corrected” by the decoder equals the Hamming distance between such random point and the nearest codeword (here the quotes in “corrected” indicate that the decoder may produce the wrong codeword). Therefore, the number of errors is distributed as a binomial random variable \(B \sim B(23,0.5)\) conditioned to \(B \leq 3\), so the probability that there are \(e\) errors is\[2^{-11}\binom{23}{e},\qquad e=0,1,2,3.\] These probabilities are as follows: 0 errors, 0.00049; 1 error 0.011; 2 errors, 0.12; 3 errors, 0.86. We see that in the case when \(\hat{u}_0\) has uncorrectable errors, then most of the time the decoding of \(\hat{u}_1\) “corrects” 3 errors. Thus, we can use the number of errors obtained by the Golay(23,12) decoder as an indicator of whether \(\hat{u}_0\) is correct or not.
The specifications define the conditions to decide if \(\hat{u}_0\) is likely to have uncorrected errors and the frame has to be discarded as follows. Let \(\epsilon_j\), \(j=0,1\), be the number of errors corrected by the Golay decoder for \(\hat{u}_j\). Put \(\epsilon_T = \epsilon_0 + \epsilon_1\). Then the frame is discarded if the Golay(24,12) decoding of \(\hat{u}_0\) failed or if \(\epsilon_0 \geq 2\) and \(\epsilon_T \geq 6\). This is a strange way of writing the conditions, because \(\epsilon_j \leq 3\), so the last two conditions are actually equivalent to \(\epsilon_0 = \epsilon_1 = 3\), meaning that both decoders corrected the maximum number of errors.
I have done some simulations to study the performance of the P25 vocoder FEC. The calculations have been done in this Jupyter notebook, using the Golay decoders that I have introduced in recent posts for Golay(24,12) and Golay(23,12).
Here I compare four encoding and decoding schemes. One of them is the P25 vocoder FEC specification. Another is a naïve approach where \(\hat{u}_0\) is encoded with Golay(24,12) and \(\hat{u}_1\) is encoded with Golay(23,12), but no additional measures are taken (i.e., we set \(\hat{m}_1 = 0\) and we only discard a frame when Golay(24,12) decoding of \(\hat{u}_0\) fails). Another variation uses the PN word \(\hat{m}_1\) but still only drops frames when decoding of \(\hat{u}_0\) fails (note that this is rather silly, since it makes more difficult the decoding of \(\hat{u}_1\) for no good). The last variation uses the rule \(\epsilon_0 = \epsilon_1 = 3\) to drop frames but doesn’t use the PN word.
In these simulations, a large number of random vectors \(\hat{u}_0\) and \(\hat{u}_1\) are generated and encoded using the four methods outlined above. Error patterns using a bit error probability \(p\) are generated and added to the encoded words \(\hat{c}_0\) and \(\hat{c}_1\) and decoding is attempted, taking note of the rate at which several situations happen. The results are summarised in the graphs below.
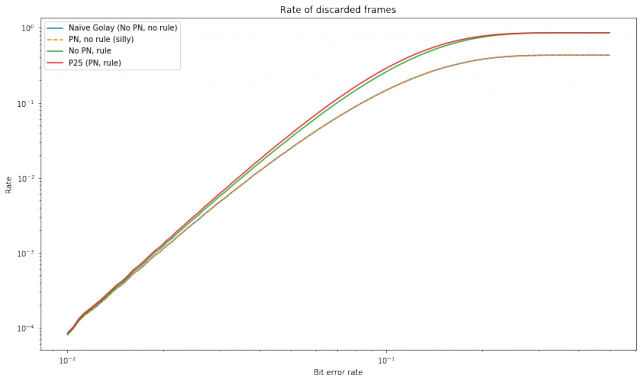
The first graph shows the number of discarded packets. We see that the naïve scheme and the silly scheme (which only uses PN) discard the same number of packets, which is not difficult to explain. The \(\epsilon_0 = \epsilon_1 = 3\) rule causes much more packets to be dropped, especially at high bit error rates. The full P25 specification drops even slightly more packets, owing to the corruption of \(\tilde{u}_1\) when decoding of \(\hat{u}_0\) fails.
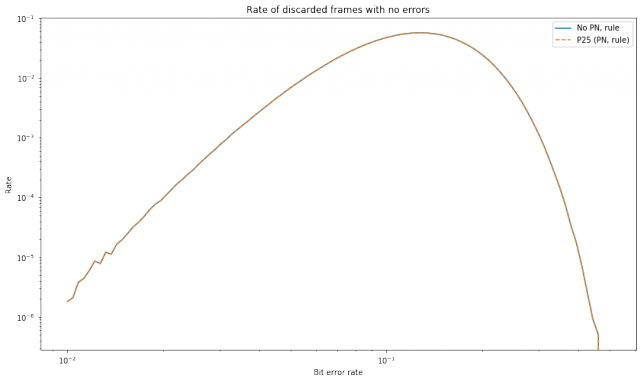
The next graph shows the number of false positives, or frames which were correctly decoded but nevertheless dropped. We only show the results for the methods using the \(\epsilon_0 = \epsilon_1 = 3\) rule, since the other methods do not give any false positives. Note that for very high bit error rates, on the order of 0.1, there are a lot of false positives. However, for smaller bit error rates, false positives quickly start to become irrelevant.
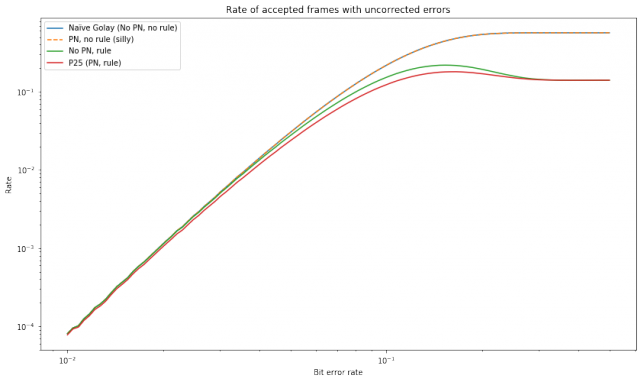
The graph below shows the number of false negatives, or the number of frames which were accepted but had uncorrected errors. Here we see that the P25 frame dropping rule makes a large improvement at high bit error rates, but the improvement is much lower for low bit error rates.
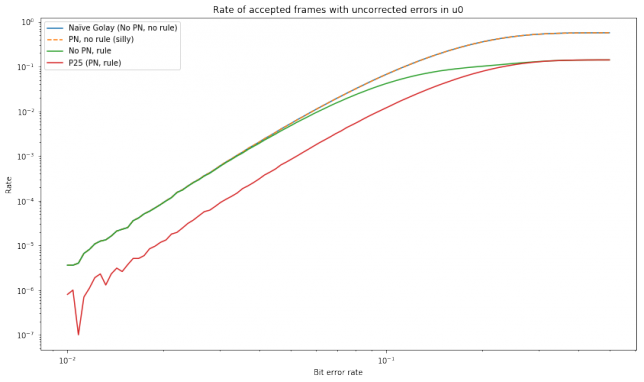
False negatives can be classified according as to whether they had errors in \(\tilde{u}_0\) or in \(\tilde{u}_1\) or both. The next graph shows the number of accepted frames that had errors in \(\tilde{u}_0\). We see that using the full P25 specification reduces the rate almost an order of magnitude. This means that the P25 vocoder FEC satisfies well its main goal of detecting frames with incorrect \(\tilde{u}_0\).
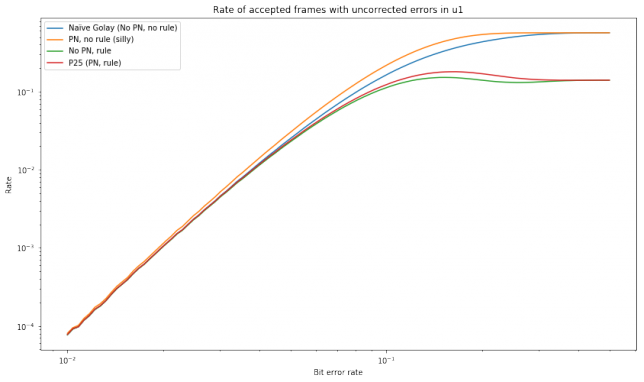
Last, we show the number of accepted frames that had errors in \(\tilde{u}_1\). This graph is interesting because all the four schemes studied have different behaviour. For low bit error rates, the behaviour of all of them is nearly the same, showing that the P25 scheme doesn’t provide much improved protection against corruptions in \(\tilde{u}_1\).
Going back to using Codec2 on DMR, as I mentioned, the current situation is that all equipment implements the P25 half rate vocoder specifications, so codec agnosticism is lost up to some extent. The main issue is that repeaters expect a data stream encoded according to the P25 vocoder FEC specifications and perform FEC decoding before repeating the data. Therefore, we don’t have the full 3600bps at our disposal, since we must follow the P25 vocoder FEC specifications and introduce Codec2 by piggybacking onto the 2450bps AMBE stream. Indeed, it is not clear that we can use the full 2450bps, since the specifications also mention that frames with \(120 \leq \hat{b}_0 \leq 123\) are invalid and should be dropped. Here \(\hat{b}_0\) is a 7bit field that indicates the frame type. Its 4 most significant bits are stored in \(\hat{u}_0\) and its 3 least significant bits are stored in \(\hat{u}_3\). It would be good to know if repeaters drop frames with \(120 \leq \hat{b}_0 \leq 123\) or retransmit them (so dropping is performed by the receiver). Another thing that we should know is if the repeaters perform frame repetition to fill up discarded frames or leave that task to the receiver.
Still, not all is lost. Even though the P25 vocoder FEC is designed with MBE in mind (its main design goal is to protect \(\hat{u}_0\)), there is a lot of room in 2450bps to fit a Codec2 stream. The standard Codec2 stream is only 1300bps, so a lot of additional FEC can be added and still make the stream fit into 2450bps. It is a good question how to make the best use of the P25 vocoder FEC, since its frame dropping rules would still be enforced.