Reed-Solomon bug in Queqiao

Queqiao is the communications relay satellite for the Chang’e 4 Chinese lunar lander mission to the far side of the Moon. It is in a halo orbit around the Earth-Moon Largrange L2 point and provides communications to the lander in Von Kármán crater.

Queqiao transmits telemetry in S-band, using the frequency 2234.5 MHz. The modulation and coding is similar to other recent Chinese probes, such as Chang’e 5 and Tianwen-1. Here I report an interesting bug that I found in the Reed-Solomon encoding performed by Queqiao.

Queqiao transmits telemetry using PCM/PM/PSK modulation with a subcarrier frequency of 65536 Hz and a baudrate of 2048 baud. CCSDS concatenated coding is used with a frame size of 220 information bytes, so that each frame takes exactly 2 seconds to transmit. This is very similar to the modulation and coding used by Chang’e 5 and Tianwen-1. In particular, Chang’e 5 was using exactly this modulation and coding during the lunar mission. Interestingly, Queqiao doesn’t seem to transmit CCSDS TM Space Data Link or AOS frames, but rather uses a custom framing.

In this post we will use a recording done with one of the Allen Telescope Array 6.1 metre dishes on 2021-09-19. The recording is published in this dataset in Zenodo.

The GNU Radio decoder flowgraph that we use is shown below. It can be downloaded here.

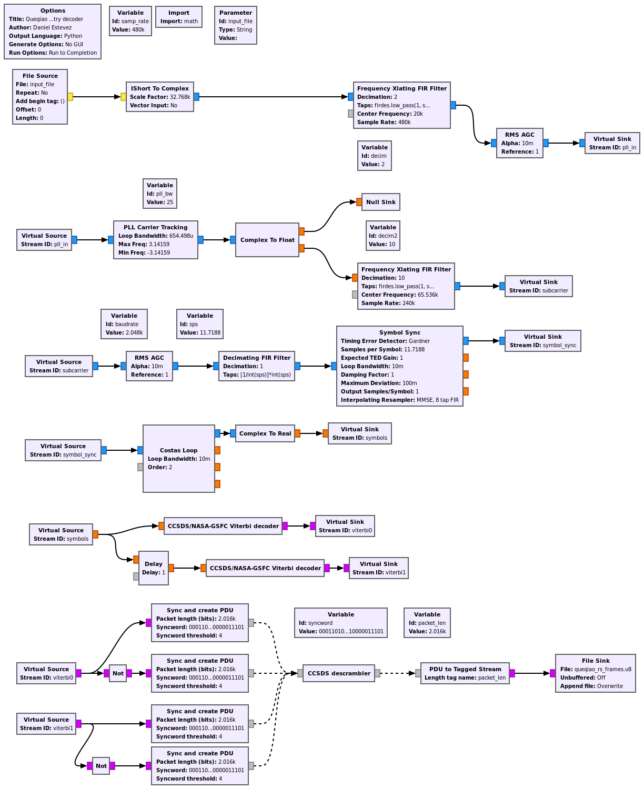
This flowgraph doesn’t perform Reed-Solomon decoding, and outputs the Reed-Solomon codewords to a file, since we’re interested in looking at the codewords in detail. This is done using Phil Karn KA9Q’s libfec through ctypes from a Python Jupyter notebook. The flowgraph is run on the recording of the X polarization of the signal only, since the SNR is good enough that we don’t need to combine both polarizations to synthesize circular polarization.

Queqiao uses for its Reed-Solomon code the dual basis, as specified in the CCSDS documents, so we must use the decode_rs_ccsds() function from libfec to perform decoding.

As a first step, we perform Reed-Solomon decoding and look at the number of byte errors corrected by the decoder. A value of -1 corresponds to a decode error. What we see is that most of the frames have 4 byte errors, while we would expect 0 byte errors, since the signal is strong enough.

There are a bunch of decode errors that probably correspond to false ASM detections, since 4 bit errors are allowed in the ASM detection. These are harmless, since they don’t interfere with the correct ASM detections.

There are also some parts of the recording where there are more than 4 byte errors, and at the end we see that decoding suddenly stops. Perhaps the satellite went out of the antenna beam, since I was tracking a fixed right ascension and declination during this recording.

The question we are concerned with here is why there are always 4 errors. The reason is interesting, and there are some puzzling things along the way.

The first we do is to look at one of the frames and its decoded version, to try to see which 4 bytes the Reed-Solomon decoder has changed. This is the original frame:

03 79 16 0a 32 98 02 81 27 55 9a aa bb 02 c5 00 
00 f9 6b 00 00 00 00 a4 09 00 00 00 00 00 00 00 
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 
21 00 28 00 3e a7 02 20 ee 58 01 04 08 24 00 00 
63 00 00 00 62 00 00 00 07 92 92 00 00 db cf 25 
53 0f 00 00 08 c6 02 3b 12 95 0c 0c 30 23 fe f0 
58 28 ca 53 1a 10 1f 35 ac 4f da f8 00 00 00 00 
00 00 00 00 00 00 00 00 0f 38 2a 29 d9 49 07 07 
f9 0d 00 00 00 00 00 00 80 49 04 43 00 00 00 00 
ae 7f af ae ac af 00 00 00 00 04 04 ff c1 00 ff 
11 00 96 55 ff 01 01 01 01 01 01 01 01 01 01 76 
8f 80 02 01 01 01 01 01 01 01 01 01 01 01 01 01 
01 01 aa aa aa aa aa aa aa aa aa aa aa aa aa aa 
aa aa ee ee ee ee ee ee ee ee ee ee d2 1e ec e9 
a3 5c ae bf 0f 1e 66 47 e3 46 82 ff bf de d4 a9 
87 1e b9 26 67 58 f2 e9 4c f9 62 ab

And this is the decoder output, including the parity check bytes:

03 79 16 0a 32 98 02 81 27 55 9a aa bb 02 c5 00 
00 f9 6b 00 00 00 00 a4 09 00 00 00 00 00 00 00 
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 
21 00 28 00 3e a7 02 20 ee 58 01 04 08 24 00 00 
63 00 00 00 62 00 00 00 07 92 92 00 00 db cf 25 
53 0f 00 00 08 c6 02 3b 12 95 0c 0c 30 23 fe f0 
58 28 ca 53 1a 10 1f 35 ac 4f da f8 00 00 00 00 
00 00 00 00 00 00 00 00 0f 38 2a 29 d9 49 07 07 
f9 0d 00 00 00 00 00 00 80 49 04 43 00 00 00 00 
ae 7f af ae ac af 00 00 00 00 04 04 ff c1 00 ff 
11 00 96 55 ff 01 01 01 01 01 01 01 01 01 01 76 
8f 80 02 01 01 01 01 01 01 01 01 01 01 01 01 01 
01 01 aa aa aa aa aa aa aa aa aa aa aa aa aa aa 
aa aa ee ee ee ee ee ee ee ee ee ee d2 1e ec e9 
a3 5c ae bf 0f 1e 66 47 e3 46 82 ff bf de d4 a9 
87 1e b9 26 67 58 f2 e9 4c f9 62 b1

If we look closely, we see that only the last byte has changed, from 0xab to 0xb1. That’s somewhat weird, since the decoder tells us it has corrected 4 bytes rather than 1.

Here I’m using just the first decoded frame as a concrete example, but in the Jupyter notebook we can see that this happens with all the frames for which the decoder says that it has corrected 4 bytes.

Since we have seen that none of the information bytes have been changed by the decoder, something else we might try is to take these and run them through the encoder. We would expect to obtain the same parity check bytes that we’re seeing here. This is not what happens, though. Below we show the output of the encoder. Note that all the 32 parity check bytes are completely different from those that we have seen above.

03 79 16 0a 32 98 02 81 27 55 9a aa bb 02 c5 00 
00 f9 6b 00 00 00 00 a4 09 00 00 00 00 00 00 00 
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 
21 00 28 00 3e a7 02 20 ee 58 01 04 08 24 00 00 
63 00 00 00 62 00 00 00 07 92 92 00 00 db cf 25 
53 0f 00 00 08 c6 02 3b 12 95 0c 0c 30 23 fe f0 
58 28 ca 53 1a 10 1f 35 ac 4f da f8 00 00 00 00 
00 00 00 00 00 00 00 00 0f 38 2a 29 d9 49 07 07 
f9 0d 00 00 00 00 00 00 80 49 04 43 00 00 00 00 
ae 7f af ae ac af 00 00 00 00 04 04 ff c1 00 ff 
11 00 96 55 ff 01 01 01 01 01 01 01 01 01 01 76 
8f 80 02 01 01 01 01 01 01 01 01 01 01 01 01 01 
01 01 aa aa aa aa aa aa aa aa aa aa aa aa aa aa 
aa aa ee ee ee ee ee ee ee ee ee ee a1 e7 33 a8 
2a cb ce 5e 76 b4 10 5c 6e e4 84 07 6b f6 50 ac 
c3 d5 f4 18 52 3a e4 18 cc 7f 4b ec

At first I found this very confusing. How could it be that we have two different versions of a Reed-Solomon codeword, having the same information bytes but totally different parity check bytes, and that the decoder is able to work with both of them? (In one of the versions it mysteriously corrects 4 errors, while in the other one it corrects 0 errors).

The explanation has to do with how virtual fill of Reed-Solomon codewords works. The CCSDS Reed-Solomon code is a (255, 223) code, which means that we take 223 information bytes, compute 32 parity check bytes, and concatenate them to obtain a 255 byte codeword. An important property of the Reed-Solomon code is that it is cyclic, meaning that every circular shift of a valid codeword is also a valid codeword.

The way to use shorter frame sizes with this Reed-Solomon code is through virtual fill, which is just zero-padding. Basically, the transmitter zero pads the information bytes it wants to send in order to obtain 223 information bytes and then encodes using the (255, 223) code. The padding bytes are not sent over the air. Only the original information bytes plus 32 parity check bytes are sent. The receiver knows the size of the frame, so it knows how many padding bytes were added, and can add the padding back before decoding.

Now, the convention about where to add this padding is that in the full 255 byte encoded codeword the original information bytes and the 32 parity check bytes should be adjacent, with the parity check bytes following the information bytes. It doesn’t really matter if the padding is at the beginning or at the end of the 255 byte codeword. Since the code is cyclic, we can move from one arrangement to the other by using a circular shift, and once we strip the padding the result is the same.

Typically, the transmitter will add the padding before the original information bytes (and this is usually the way that virtual fill is explained), since by doing this and running the encoder it obtains a codeword that has the structure padding-information-checkbytes. The information and check bytes are adjacent and it can just strip the padding. If it added the padding after the information bytes, it would obtain a codeword with the structure information-padding-checkbytes. This doesn’t really work, because the information and check bytes are not adjacent, and there is not a way to fix this using circular shifts. On the other hand, the receiver receives something that has the structure information-checkbytes. It can add the padding either at the beginning (before information) or at the end (after checkbytes), and then decode normally, since both options are a circular shift of each other.

Coming back to Queqiao, we see that the Reed-Solomon encoder says it is correcting 4 bytes, but we only see that one byte has been changed. Moreover, the number of padding bytes used by Queqiao is 3. So we suspect something strange is going on with these padding bytes.

To investigate what happens with the padding, we take the 252 byte codewords that our flowgraph has obtained, add 3 0x00 bytes before them to obtain 255 byte codewords, and run these through the decoder. This is what we get for the first codeword:

cf fc 1d 03 79 16 0a 32 98 02 81 27 55 9a aa bb 
02 c5 00 00 f9 6b 00 00 00 00 a4 09 00 00 00 00 
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 
00 00 00 21 00 28 00 3e a7 02 20 ee 58 01 04 08 
24 00 00 63 00 00 00 62 00 00 00 07 92 92 00 00 
db cf 25 53 0f 00 00 08 c6 02 3b 12 95 0c 0c 30 
23 fe f0 58 28 ca 53 1a 10 1f 35 ac 4f da f8 00 
00 00 00 00 00 00 00 00 00 00 00 0f 38 2a 29 d9 
49 07 07 f9 0d 00 00 00 00 00 00 80 49 04 43 00 
00 00 00 ae 7f af ae ac af 00 00 00 00 04 04 ff 
c1 00 ff 11 00 96 55 ff 01 01 01 01 01 01 01 01 
01 01 76 8f 80 02 01 01 01 01 01 01 01 01 01 01 
01 01 01 01 01 aa aa aa aa aa aa aa aa aa aa aa 
aa aa aa aa aa ee ee ee ee ee ee ee ee ee ee d2 
1e ec e9 a3 5c ae bf 0f 1e 66 47 e3 46 82 ff bf 
de d4 a9 87 1e b9 26 67 58 f2 e9 4c f9 62 b1

Here we readily see the 4 bytes that the Reed-Solomon decoder has corrected: the last one (which we already knew about), and the three 0x00 padding bytes at the beginning, which have been corrected to 0xcffc1d.

This is quite weird and interesting. When there is virtual fill being used, the decoder shouldn’t need to change the padding bytes. These are known to be zeros, and are not transmitted over the air. So this indicates that there is a bug in the encoder, and it isn’t really using zeros as padding, so the receiver’s decoder must correct the padding bytes to account for that.

This also explains why when we re-encoded the information bytes we obtained some completely different parity check bytes. Our encoder is really using zeros as padding, so this changes completely the parity check bytes, as we know that a small change in the 223 information bytes will completely change all the 32 parity check bytes.

The three bytes we have obtained, 0xcffc1d, are the end of the 32-bit ASM 0x1acffc1d that is used with the CCSDS concatenated frames (and that Queqiao is transmitting right before the Reed-Solomon codeword). This doesn’t seem to be a coincidence. It looks like a buffer handling problem where instead of having the three 0x00 bytes before the information bytes in the Reed-Solomon encoder, we have 0xcffc1d, which are the three bytes that should be sent immediately before the codeword.

However, this doesn’t explain why the last byte in the codeword is also wrong. Perhaps the last byte doesn’t really belong to the 255 byte codeword. If so, the codeword would start one byte earlier, and we would have 4 instead of 3 virtual fill bytes. Perhaps by doing so we will see the first virtual fill byte being corrected to 0x1a (the first byte of the ASM).

To test this idea, we drop the last byte of each 252 byte codeword and add 4 0x00 bytes to the beginning of the codeword. This is what we get for the first codeword:

b1 cf fc 1d 03 79 16 0a 32 98 02 81 27 55 9a aa 
bb 02 c5 00 00 f9 6b 00 00 00 00 a4 09 00 00 00 
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 
00 00 00 00 21 00 28 00 3e a7 02 20 ee 58 01 04 
08 24 00 00 63 00 00 00 62 00 00 00 07 92 92 00 
00 db cf 25 53 0f 00 00 08 c6 02 3b 12 95 0c 0c 
30 23 fe f0 58 28 ca 53 1a 10 1f 35 ac 4f da f8 
00 00 00 00 00 00 00 00 00 00 00 00 0f 38 2a 29 
d9 49 07 07 f9 0d 00 00 00 00 00 00 80 49 04 43 
00 00 00 00 ae 7f af ae ac af 00 00 00 00 04 04 
ff c1 00 ff 11 00 96 55 ff 01 01 01 01 01 01 01 
01 01 01 76 8f 80 02 01 01 01 01 01 01 01 01 01 
01 01 01 01 01 01 aa aa aa aa aa aa aa aa aa aa 
aa aa aa aa aa aa ee ee ee ee ee ee ee ee ee ee 
d2 1e ec e9 a3 5c ae bf 0f 1e 66 47 e3 46 82 ff 
bf de d4 a9 87 1e b9 26 67 58 f2 e9 4c f9 62 

We see that the first byte we get in the decoder output is not 0x1a, but rather 0xb1. The byte we get in this position changes in every frame and it seems quite random. It appears to be uniformly distributed and I haven’t been able to find any relationship to the bytes in adjacent frames.

In summary, it seems that there is a bug in the Reed-Solomon encoder of Queqiao that causes the encoder to use 0xcffc1d instead of zeros for three virtual fill bytes, and additionally there is another wrong byte in the codewords for which we don’t have a good explanation.

The material for this post is available in this repository, including the Jupyter notebook and the file with the Reed-Solomon codewords.