LDPC code design for my QO-100 narrowband modem

A couple months ago I presented my work-in-progress design for a data modem intended to be used through the QO-100 NB transponder. The main design goal for this modem is to give the maximum data rate possible in a 2.7 kHz channel at 50 dB·Hz CN0. For the physical layer I settled on an RRC-filtered single-carrier modulation with 32APSK data symbols and an interleaved BPSK pilot sequence for synchronization. Simulation and over-the-air tests of this modulation showed good performance. The next step was designing an appropriate FEC.

Owing to the properties of the synchronization sequence, a natural size for the FEC codewords of this modem is 7595 bits (transmitted in 1519 data symbols). The modem uses a baudrate of 2570 baud, so at 50 dB·Hz CN0 the Es/N0 is 15.90 dB. In my previous post I considered using an LDPC code with a rate of 8/9 or 9/10 for FEC, taking as a reference the target Es/N0 performance of the DVB-S2 MODCODs. After some performing some simulations, it turns out that 9/10 is a bit too high with 7595 bit codewords (the DVB-S2 normal FECFRAMEs are 64800 bits long, giving a lower LDPC decoding threshold). Therefore, I’ve settled on trying to design a good rate 8/9 FEC. At this rate, the Eb/N0 is 9.42 dB.

Some time ago, I twitted asking for good references to learn LDPC code design. The suggestions there together with the comments I exchanged with Bill Cowley VK5DSP over email have been very helpful. Several people recommended Sarah Johnson‘s book “Iterative Error Correction“. I’ve already finished reading that book and I can recommend it as a good self-contained introduction to LDPC, Turbo and RA codes. Another book that people recommended is “Channel Codes: Classical and Modern” by William Ryan and Shu Lin, though I haven’t started reading it yet.

As in the case of the modulation, I am trying to draw a lot of inspiration on DVB-S2, so I am using the DVB-S2 LDPC codes as a reference of what kind of performance is possible. DVB-S2 uses LDPC codes with codeword sizes of 64800 for the normal FECFRAMEs and 16200 bits for the short FECFRAMEs. The short FECFRAMEs have a degradation of 0.2 to 0.3 dB in comparison with the normal FECFRAMEs. Since the codeword size of 7595 bits that we will be considering in this post is shorter, we expect even more degradation. The LDPC codes used by DVB-S2 are described in Section 5.3.2 of the EN 302 307-1 ETSI standard.

To perform simulations I am using AFF3CT on a Ryzen 7 5800X CPU. I am running most of the simulations using the following parameters:

aff3ct-3.0.1 --sim-type BFER -C LDPC --enc-type LDPC_H \
  -m 9.0 -M 9.7 -s 0.1 --dec-implem SPA \
  --dec-h-path code_h.alist -e 100 -i 2000 \
  --dec-type BP_FLOODING \
  --mdm-const-path 32apsk.mod --mdm-type USER \
  --mdm-max MAXSS

These give a BER and FER simulation over a range of Eb/N0 between 9.0 and 9.7 dB, in steps of 0.1 dB. The simulation at each step stops when 100 frame errors are collected, which is deemed as large enough to give a good estimate of the FER. The decoder uses the sum-product algorithm with flooding belief propagation and a maximum of 2000 iterations. These parameters are mainly taken from this simulation of an (8000, 4000) LDPC code and I think they are representative of a decoder implementation with good sensitivity. For this modem, the speed of the decoder is not so important because the bitrate will be rather low. Sensitivity is quite important, though, so it makes sense to trade speed for sensitivity.

The simulation uses a custom constellation to represent the 32APSK constellation (see here). In these tests I am using the DVB-S2 32APSK constellation for rate 9/10, which is what I was using for the tests in my previous post also. In DVB-S2, the relative sizes of the three concentric rings that form the 32APSK constellation depend on the coding rate. I should also test with the 8/9 constellation, given that here I intend to use an 8/9 LDPC code, however this constellation is quite close to the 9/10, so I don’t expect any major differences. Perhaps I should also give more thought to the interplay between the definition of the constellation and the FEC, to see if there is some room for improvement there. Probably the DVB-S2 constellations are well optimized already, but it would be good to understand how they were optimized.

To demodulate the symbols into LLRs, I am using the MAXSS function, which is a max* function modified to avoid numerical stability. I have compared it to the simpler MAX function and there is a small but noticeable improvement in sensitivity with MAXSS.

To help me in designing LDPC codes, I have created a Rust crate called ldpc-toolbox. This is early work in progress and I still want to add more functionality and polish its usage before publishing a version to crates.io. However, it has already been quite useful in its present state. I have decided to use Rust instead of Python for this because it will definitely be faster (some constructions involve large random searches or the calculation of graph cycles) and it will serve me to gain more experience with Rust, which is a language that I have started using some months ago (for those interested in learning Rust, definitely check out the Rust Programming Language book).

One of the things that ldpc-toolbox can do is to construct alists for all the DVB-S2 LDPC codes, since AFF3CT only includes some of the codes. This can be done by running

ldpc-toolbox-dvbs2 --rate 3/4 > /tmp/code.alist

to write the alist of the parity check matrix to a file. This tool also supports the --girth parameter to compute the girth of the Tanner graph, which can be used to show that all the DVB-S2 codes avoid 4-cycles and have a girth of 6.

Another thing that can be done with ldpc-toolbox is to use the popular random construction introduced by MacKay and Neal in the 1996 paper “Near Shannon Limit Performance of Low Density Parity Check Codes“. This construction involves adding the rows of the parity check matrix one by one. The rows are added with the desired column weight and only considering columns which have not yet reached the desired row weight. Some properties, such as satisfying a minimum girth, can be imposed during the construction.

The main inspiration to design LDPC codes for the QO-100 modem using the MacKay-Neal construction comes from Figure 7.9 in Sarah Johnson’s book, which is reproduced here for reference.

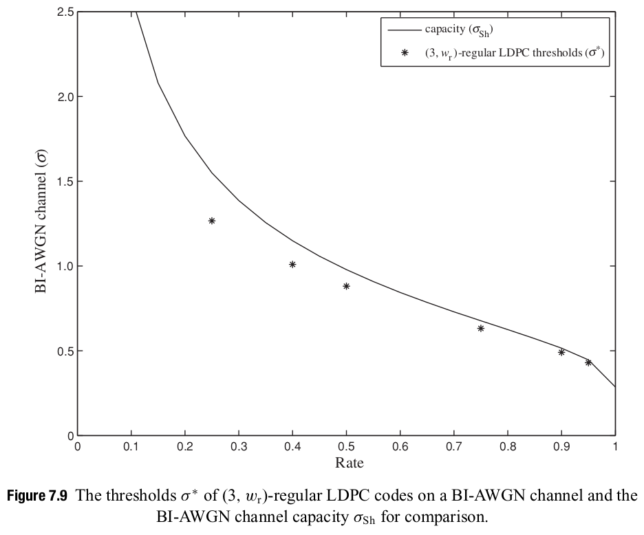
In this figure, the ensemble threshold simulated using density evolution is compared to the Shannon capacity for regular codes of different rates and column weight 3. This shows that this family of codes is quite close to channel capacity for high rates. In fact, column weight 3 is the optimal for regular codes with rates smaller than 0.95, as discussed in the previous page of the book.

Moreover, it is known that for long codes random constructions tend to work well. Therefore, a MacKay-Neal construction with column weight 3 and row weight 27 (to give a rate of 8/9) should work quite well. There is perhaps a small margin for improvement in the code threshold by optimizing the degree distribution. Other improvements that can be done regard the code structure, which helps simplify the encoder and decoder (DVB-S2 LDPCs have much more structure than random codes), and the error floor performance. For this modem, I am not concerned with the complexity of the encoder and decoder, and probably it is not so critical to have a very low error floor. As we will see, it is probably preferable to try to lower the waterfall threshold.

For a codeword size of 7595 bits, we can choose a full-rank parity check matrix with 844 rows, which gives a rate very close to 8/9. For a column weight of 3, we will have 22785 ones in the matrix. A row weight of 27 would give 22788 ones. Therefore, most of the rows will have a weight of 27, but three rows will need to have weight 26. This kind of code can be constructed with ldpc-toolbox by doing

ldpc-toolbox-mackay-neal 844 7595 27 3 0 --search

Here the --search parameter instructs the decoder to try different seeds until the construction succeeds, because since rows are filled in completely randomly we could get stuck at some point. A minimum girth of 6 can be imposed by adding the parameters

--min-girth 6 --girth-trials 1000

Besides generating LDPC codes for the modem, it is also interesting to generate codes with the same size as the DVB-S2 short FECFRAMEs, in order to compare the performance of the more regular IRA-like DVB-S2 codes with random MacKay-Neal construction codes. These can be generated with

ldpc-toolbox-mackay-neal 1800 16200 27 3 0 --search \
  --min-girth 6 --girth-trials 1000 --uniform

The --uniform parameter tries to fill rows more uniformly so that the algorithm is less prone to getting stuck. This is important because 1800 is exactly 16200/9, so in the end all the rows will be filled to weight exactly 27.

The figure below shows the results of simulating the codes described above with AFF3CT and plotting the results with PyBER. The results and alists can be found in the ldpc folder of my qo100-modem repository.

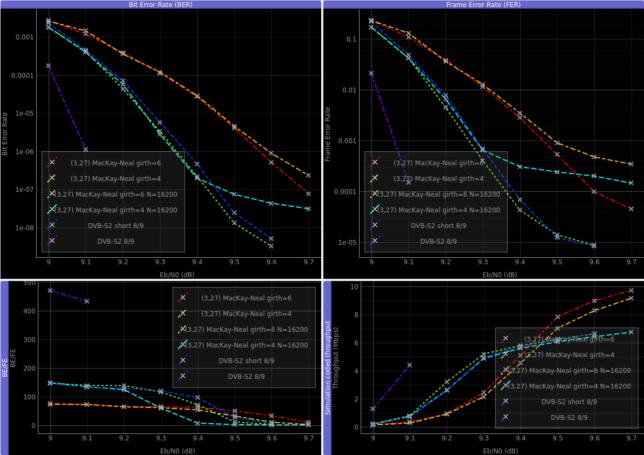
In red and orange we see the (7595, 6751) random codes with girths 6 and 4 respectively. We see that the performance of the girth 4 code degrades, especially the FER, when the Eb/N0 increases. The same happens with the (16200, 14400) random codes, depicted in green and light blue. These have the same size as the DVB-S2 short FECFRAMEs and show an improvement of 0.2 to 0.25 dB in comparison to the shorter (7595, 6751) codes. The DVB-S2 8/9 short FECFRAME code, shown in dark blue, has slightly worse performance than the girth 6 random code of the same size. This indicates that the performance of random MacKay-Neal constructions of these characteristics is quite good. Finally, the DVB-S2 8/9 normal FECFRAME is shown in purple for comparison. The simulation of this code is already cut at 9.1 dB Eb/N0, since at 9.2 dB the FER is already very low to produce 100 frame errors in a reasonable time. We can see that this (64800, 57600) code has roughly 0.3 dB improvement in comparison with the (16200, 14400) codes.

I have also experimented with searching random MacKay-Neal constructions (by trying different random seeds) that produce results better than the average. There seems to be a small improvement when the best out of thousands of codes are selected, but I think more work is needed regarding this idea. I don’t expect any large improvements. Since the code is large, advantages in the code structure tend to average out, and so all the random codes perform rather similarly.

I am not completely happy with the results, since at the target Eb/N0 of 9.4 dB we have a BER of 3e-5 and a FER of 3e-3. This doesn’t look too bad really. Since frames take 603 ms to transmit, we would only see an average of 18 frame errors per hour, which is probably acceptable for most uses one can imagine in amateur radio. The problem is that we don’t have any link margin. With only 0.2 dB of losses, the FER becomes 4%.

In the end, the reference of 50 dB·Hz CN0 was taken as a ballpark estimate of the power of the SNR of the BPSK beacon. However, this estimate depends somewhat on the characteristics of the receiving station and may vary by a fraction of a dB or even 1 dB. I think that in practice it will be acceptable that this modem is used at a slightly higher power than the beacon (and by slightly I really mean a fraction of a dB), so perhaps the threshold of the (7595, 6751) code I have is already acceptable. Probably some over-the-air tests are appropriate to see how well the modem works in practice and measure implementation losses.

I do not really want to make the codewords longer, since that would make them more than one second long, which seems too much for many applications that require some interactivity. I also like the rate of 8/9, since it gives a user bitrate of 11193.8 bps, which is still above the 11 kbps mark (this seems “good marketing” for the modem). In fact with 7/8 we’re still above 11 kbps. However, the improvement in moving from 8/9 to 7/8 is only 0.07 dB increase in Eb/N0 for the same Es/N0, so it is probably not worth it.

Some other things I want to implement in ldpc-toolbox are the progressive edge growth (PEG) random construction algorithm, and some form of density evolution, perhaps to try to optimize the degree distribution of the modem. I don’t think that any of this will give a large improvement, but it will be interesting to see the results.