In my previous post I looked at the BGDs and related topics for the Galileo satellites. We saw that satellite E24 has atypically large BGDs, but everything else seems fine and consistent with that satellite. However, Bert Hubert from galmon.eu shows that several RTCM sources broadcast a clock correction of around -5ns for E24. Here we look at the possible causes for that correction, and discuss whether it might be problematic.
I’ll start off with a correction to my previous post. In there, we saw that not only E24 has atypically large \(BGD(\mathrm{E1}, \mathrm{E5a})\) and \(BGD(\mathrm{E1}, \mathrm{E5b})\), but also the difference \(BGD(\mathrm{E1}, \mathrm{E5a}) – BGD(\mathrm{E1}, \mathrm{E5b})\) is atypically large (around 5ns). I said that this causes different delays in the E5a and E5b signals, so users of the combined AltBOC signal may need to take it into account.
However, if we look at the DCBs for E1-E5a and E1-E5b, we will see that they are pretty similar. In fact, the DCB for E1-E5a is -36.1ns, and the DCB for E1-E5b is -35.8ns, so their difference (which gives the DCB for E5b-E5a) is only -0.25ns. Hence the difference of delays between E5a and E5b is small. In hindsight, this is to be expected. The E5a and E5b signals are really sidebands of the same AltBOC modulation, which is passed through the same power amplifier and filter chain. The response of these will vary slightly with frequency, but a large difference of delays is not to be expected unless something has gone really wrong.
This remark gives us more insight into why the BGDs for E24 are rather different. As we have said, typically we will have \(DCB(\mathrm{E1} – \mathrm{E5a}) \approx DCB(\mathrm{E1} – \mathrm{E5b})\). Now,\[\begin{split}BGD(\mathrm{E1}, \mathrm{E5a}) &- BGD(\mathrm{E1}, \mathrm{E5b}) = \\ &\frac{DCB(\mathrm{E1} – \mathrm{E5a})}{1 – \left(\frac{f_{\mathrm{E1}}}{f_{\mathrm{E5a}}}\right)^2} – \frac{DCB(\mathrm{E1} – \mathrm{E5b})}{1 – \left(\frac{f_{\mathrm{E1}}}{f_{\mathrm{E5b}}}\right)^2} \approx \\ &DCB(\mathrm{E1} – \mathrm{E5a}) \left[ \frac{1}{1 – \left(\frac{f_{\mathrm{E1}}}{f_{\mathrm{E5a}}}\right)^2} – \frac{1}{1 – \left(\frac{f_{\mathrm{E1}}}{f_{\mathrm{E5b}}}\right)^2}\right].\end{split}\]The number in square brackets is approximately 0.16, so this means that the difference between BGDs is proportional to either one of the DCBs (assuming both DCBs are very similar). We can also write this in terms of BGDs as \[\begin{split}BGD(\mathrm{E1}, \mathrm{E5a}) &- BGD(\mathrm{E1}, \mathrm{E5b}) \approx \\ &BGD(\mathrm{E1}, \mathrm{E5a}) \left[ 1 – \frac{1 – \left(\frac{f_{\mathrm{E1}}}{f_{\mathrm{E5a}}}\right)^2}{1 – \left(\frac{f_{\mathrm{E1}}}{f_{\mathrm{E5b}}}\right)^2}\right].\end{split}\]The number in square brackets is approximately -0.13.
So everything works out nicely for E24. It has a \(BGD(\mathrm{E1}, \mathrm{E5a})\) of approximately 45ns, and so the difference between BGDs must be on the order of -5.8ns. Most of the other Galileo satellites respect this proportion between the BGDs, which is a consequence of the delay between E5a and E5b being very small. If we look again at the plot of BGDs shown in the previous post, we see that the E5a BGD is usually a bit smaller than the E5b BGD.
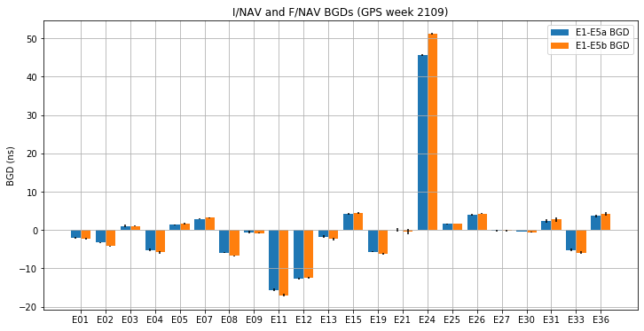
The atypical case is E12, which has an E5a BGD slightly larger than the E5b BGD. This is caused by a significantly large difference of delays between E5a and E5b, which can be seen in the plot of DCBs.
Let’s now turn back of the topic of RTCM clock corrections. The RTCM protocol includes message type 1241 to send clock corrections to the Galileo broadcast ephemerides. More information can be found in this presentation. Basically, a clock correction is formed by polynomial coefficients \(C_0, C_1, C_2\) and a base time \(t_0\), so that the correction in metres at time \(t\) is given by \[\delta C (t) = C_0 + C_1 (t – t_0) + C_2 (t-t_0)^2.\]The correction is applied by replacing the satellite clock bias \(\Delta t_{SV}(X) (t)\) computed with the broadcast parameters by \(\Delta t_{SV}(X) (t) + c^{-1}\delta C(t)\).
An important remark is that this correction is only valid for a particular choice of ionosphere-free combination or single frequency \(X\). Apparently, the RTCM provider has the freedom to choose to what \(X\) their \(\delta C\) refers to, and this choice is implicit rather than indicated in the RTCM message. Therfeore, the RTCM message should be used to correct the appropriate broadcast clock. Whether \(\delta C\) can be scaled in order to correct another broadcast clock will be discussed below.
For this post, we will be looking only at the \(C_0\) term of the RTCM clock correction. Our main point is to investigate why the main RTCM sources send a \(C_0\) of around -5ns for E24. As shown by Bert, this happens for the Spaceopal NAVCAST, the CNES PPP-wizard caster, DLR RETICLE, and to some extent for the CAS Wuhan RTCM service (more details below), so here we’ll only be looking at the Spaceopal data.
A \(C_0\) term of around -5ns means that some broadcast satellite clock model \(\Delta t_{SV}(X)\) has a +5ns error, so that when \(\delta C\) is added to the broadcast model, the error cancels out. Therefore, it is best to start by investigating the broadcast clocks for E24 and checking if there is anything wrong with them.
To do so, we use precise clock products as our best proxy for the actual clock of the satellites. We will be using CLK files from CODE. By subtracting the broadcast \(a_{f0}\) term minus the clock obtained from CODE, we obtain a good indication of the error in the broadcast clock model. However, there is a subtlety here. The two terms we’re subtracting use different timescales: the \(a_{f0}\) term is referred to the GST timescale, which is specific to the Galileo constellation, while the CODE clock files use another UTC-ish timescale that is common to all the constellations in the clock file. Therefore, the difference between the GST and the CODE timescales will show up when computing \(a_{f0}\) minus the CODE clock. However, this timescale difference term is common for all the Galileo satellites. Another detail: Care must be taken in using the correct ionosphere-free combination or scaling things appropriately. The precise clocks refer to the E1-E5a combination, so we use \(a_{f0}(\mathrm{E1}, \mathrm{E5a})\) here.
In the figure below we show the difference between the broadcast \(a_{f0}\) term for the E1-E5a combination (which is transmitted in the F/NAV message) and the CODE CLK. We show E24 in red and the remaining Galileo satellites in grey as an indication of the timescale difference between GST and the CODE. As we see, this timescale difference waves around 2 and 4ns, but all the satellites are in the same band of approximately 1ns about this timescale difference. This means that the E24 broadcast clock for E1-E5a is correct and doesn’t show any constant error that may explain the -5ns RTCM corrections.
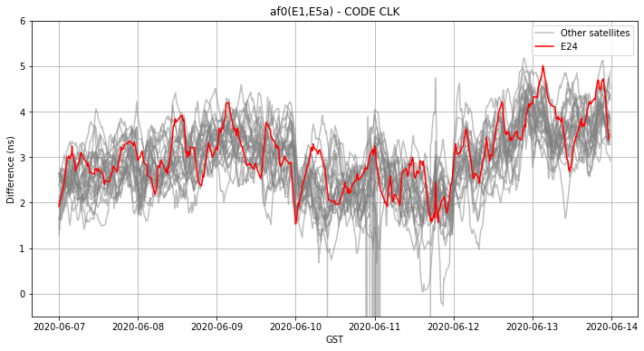
So what happens to the E1-E5b clock (which is transmitted in the I/NAV message)? Well, in my previous post I showed how to relate the E1-E5a and E1-E5b clocks using the difference of BGDs as\[\Delta t_{SV}(\mathrm{E1}, \mathrm{E5a}) – \Delta t_{SV}(\mathrm{E1}, \mathrm{E5b}) = BGD(\mathrm{E1}, \mathrm{E5a}) – BGD(\mathrm{E1}, \mathrm{E5b}).\]Thus, I checked for consistency in the broadcast clock models by showing that the differences\[a_{f0}(\mathrm{E1}, \mathrm{E5a}) – a_{f0}(\mathrm{E1}, \mathrm{E5b})\]and\[BGD(\mathrm{E1}, \mathrm{E5a}) – BGD(\mathrm{E1}, \mathrm{E5b})\]were similar for all the Galileo satellites. Therefore, the fact that the E1-E5a broadcast clock for E24 is correct also implies the correctness of the E1-E5b broadcast clock.
We are now pretty sure that the E24 broadcast clocks are correct and do not have any constant error that resembles 5ns. Yet the RTCM providers are sending a -5ns correction, but for what clock? As mentioned above, RTCM providers have the freedom to send corrections specific to any frequency combination or single frequency they want to. Bert has run some questions with Spaceopal and they said that their RTCM corrections refer to the E1-E5a clock. If we take this literally, then it is wrong: the E1-E5a broadcast clock has by no means a 5ns error.
So where could this -5ns value come from? Well, it is interesting to note that the difference between BGDs has this value. The figure below shows a number of different things, all of them centred around -5.5ns. In blue we show the \(C_0\) term for the Spaceopal RTCM. The only modification is the conversion from metres to ns. In orange, we show the difference between broadcast \(a_{f0}\) terms for E1-E5a and E1-E5b. In green, we show the difference between broadcast BGDs for E1-E5a and E1-E5b. Finally, in red we show the BGD difference computed by using the Wuhan DCBs.
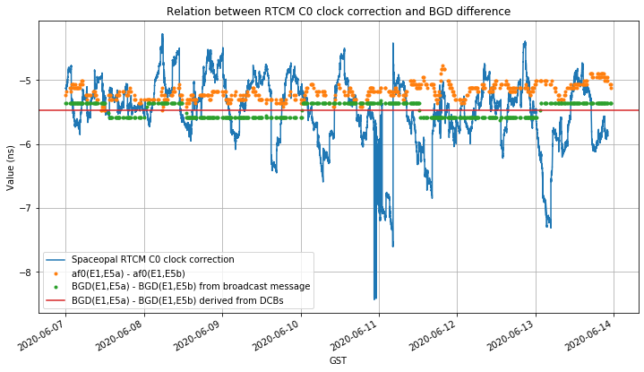
The calculation with the DCBs should give the best approximation to the real BGD difference. The difference of BGDs included in the navigation message is pretty close to this value and in fact seems to straddle it by one least-significant bit (which represents 0.23ns). As remarked above, the difference between \(a_{f0}\) terms should be very close to the difference between BGDs. Here we see some small bias of around 0.25ns, which is interesting but can probably be ignored for the purposes of this post. Finally, the RTCM \(C_0\) term moves one or two ns up and down (just because the broadcast clock model has an error that moves in this manner), but is also centred on the BGD difference.
Other than this -5ns offset, the RTCM \(C_0\) seems correct. In fact, the figure below shows the comparison between \(C_0\) and the CODE precise clock product. To do this comparison, we take the time series formed by the broadcast \(a_{f0}\) minus the CODE clock and remove its average, as a zero-order correction for the difference between the GST and CODE timescales. We also take the value of \(-C_0\) and add the difference of BGDs to it. The minus sign is needed because \(\delta C\) is used as an additive correction to the broadcast clock, so the broadcast clock error is actually \(-\delta C\).
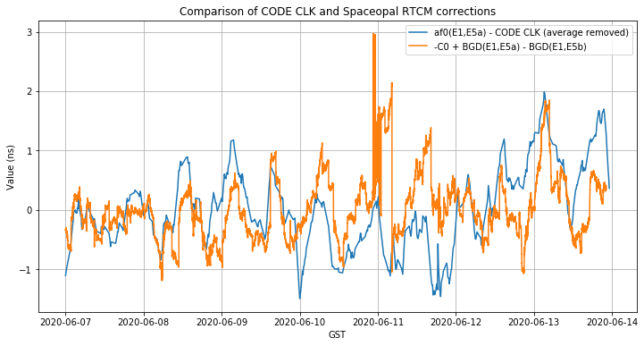
Note that there is still some difference between GST and CODE that we’ve left uncorrected, but in any case the two traces above look qualitatively rather similar. This is as much as can be expected, since the RTCM is a real time correction and the CODE precise clock is a final product, so it will be more accurate.
So what does the -5ns offset actually mean? Well, since this is equal to the difference of BGDs, which can be used to transform between the E1-E5a and E1-E5b broadcast clocks, it turns out that if we take the broadcast E1-E5b clock and add to it the RTCM correction, we end up with a better (or corrected) value for the E1-E5a clock. In formula:\[\Delta t_{SV}^B(\mathrm{E1}, \mathrm{E5b}) + c^{-1}\delta C = \Delta t_{SV}^C(\mathrm{E1}, \mathrm{E5a}),\]where we are marking with the superscript \(B\) the broadcast clock (as transmitted in the navigation message) and with the superscript \(C\) a corrected clock that should be more accurate, and is still referred to the GST timescale.
Update 2020-07-06: Originally, I made a sign mistake when deriving the formula above and wrote E5a in place of E5b and vice versa. I have now corrected this error.
The jump from the E1-E5b clock to the E1-E5a clock in the formula above is certainly weird. Users interested in staying with the same clock would find the following formulas useful:\[\Delta t_{SV}^B(\mathrm{E1}, \mathrm{E5a}) + c^{-1}\delta C – \Delta BGD= \Delta t_{SV}^C(\mathrm{E1}, \mathrm{E5a}),\]\[\Delta t_{SV}^B(\mathrm{E1}, \mathrm{E5b}) + c^{-1}\delta C – \Delta BGD= \Delta t_{SV}^C(\mathrm{E1}, \mathrm{E5b}),\]where\[\Delta BGD = BGD(\mathrm{E1}, \mathrm{E5a}) – BGD(\mathrm{E1}, \mathrm{E5b}).\]Single frequency users can subtract the appropriate BGD from both sides of these equalities to obtain their corrected clock (note that the extra terms included by \(\Delta BGD\) do not cancel out when doing so). These formulas with \(\Delta BGD\) are what galmon.eu is using now to get meaningful results for E24.
It goes without saying to say that it is important to use the formulas with the \(\Delta BGD\) term, since otherwise we end up with a satellite clock that has a -5.5ns error (roughly -1.5 metres), which is a significant problem in any application requiring precision.
So is this weird jump from the E1-E5b clock to the E1-E5a any useful? I think not. Receivers not working with E5a will only have access to the I/NAV data. Therefore, they will only have access to the E1-E5b broadcast clock model and BGD. This is all they need to work with the E1-E5b combination or single frequency on either E1 or E5b. But if they want to apply the RTCM correction and get the clock they need, they will also need knowledge of either the E1-E5a BGD or the E1-E5a broadcast clock, which is transmitted only in the F/NAV message.
Receivers working only with E5a (I reckon this is an atypical case) will only have access to the F/NAV data. As such, they have the E1-E5a broadcast clock model and BGD that they need to compute the E5a broadcast clock. However, if they want to apply the RTCM correction to get the E5a broadcast clock, then they need knowledge of either the E1-E5b BGD or the E1-E5b broadcast clock, which are in the I/NAV message.
Receivers that have access to both the I/NAV and the F/NAV message can apply the formulas above without restrictions, but what happens if the broadcast BGDs are wrong? The idea behind RTCM corrections is to protect the receiver from any problems in the broadcast data by sending appropriate corrections, so including uncorrected broadcast BGDs in the formula partially defeats this purpose.
This leads us to another ineresting topic. The RTCM protocol has also a message 1242 to send Galileo code biases. I’m not sure about the details of these messages, but I think that they can be used as DCBs, and hence as a substitute (rather than correction) for the broadcast BGDs. I don’t know whether the major RTCM providers are sending these messages (something worth checking!). If so, it might be that the biases in these messages are wrong (or let’s say “weirdly defined”) in such a way that when used together with the “weirdly defined” \(\delta C\) one obtains the appropriate clock without the need to correct with \(\Delta BGD\). This might be true only to some extent: An ionosphere-free user will not need to account for any code biases, so they will still face the \(\delta C\) weirdness problem. A single frequency user will need to throw in a correction term with a BGD computed from the RTCM code biases, so in theory it is possible that this cancels out the \(\delta C\) weirdness.
As I already mentioned above, the case of the Wuhan RTCM feed is actually more interesting. Bert has noticed that it seems that it randomly needs and doesn’t need the correction with \(\Delta BGD\). As such, it is even less useful, because one never knows how to treat it.
As a bonus, yet some more weirdness in the Galileo constellation. We have been looking at the difference in the \(a_{f0}\) terms of the broadcast clock, and saying that this must be essentially the same as \(\Delta BGD\). However, if we look at the data from the week I have studied for this series of posts, we see that there are three satellites whose \(a_{f0}\) difference goes very wrong at some point.
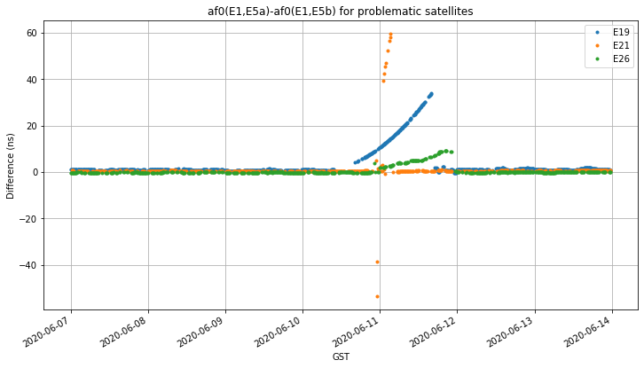
This doesn’t make much sense. The satellites only have one onboard clock active for all the signals (they have several onboard clocks as spares, but at any time they use the same one for all the navigation signals). In addition, there are the BGDs, which tell us the different delays between the navigation signals. The BGDs are parameters that change very slowly in time and so it is very difficult that estimation of them by the ground segment goes wrong (and in fact it doesn’t: we always see more or less the same BGDs for each satellite and frequency pair).
The estimation of the onboard clock by the ground segment might go wrong for a number of reasons. But still, the difference between \(a_{f0}\) terms should be equal to \(\Delta BGD\). There is no reason why one of the \(a_{f0}\)’s goes wrong and the other doesn’t, or that they both go wrong “in different ways”.
The remaining satellites show \(a_{f0}\) differences that are more or less constant and equal to their \(\Delta BGD\)’s. But still the differences move much more than \(\Delta BGD\).
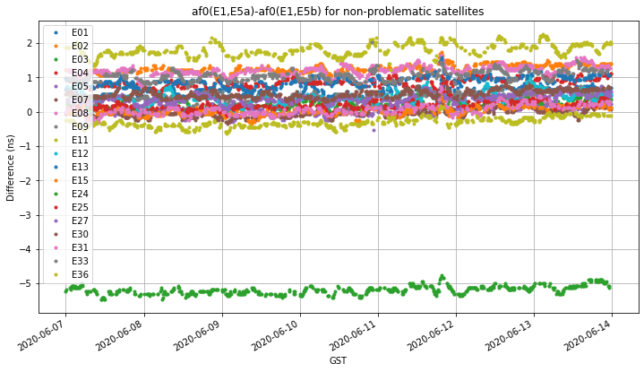
In my opinion, the \(a_{f0}\) difference should be exactly equal to \(\Delta BGD\), except for numerical precision (\(a_{f0}\) is transmitted with a resolution of \(2^{-34}\) seconds, while the BGDs have a resolution of \(2^{-32}\) seconds). Additionally, the \(a_{f1}\) and \(a_{f2}\) terms should be exactly the same for both clock models, just as the time derivatives of the BGD are deemed too small to be considered.
The calculations and data used in this post are included in the updated version of the Jupyter notebook. The Spaceopal RTCM data was kindly provided by Bert from the protobuf data stored by the galmon network. Bert and I have been working in parallel and exchanging private communication about these topics, so some of the ideas and discoveries presented here are originally from Bert and others are mine.
One comment