I have been wondering about how the DOP for the different GNSS constellation varies geographically, owing to the different number of satellites and constellation geometries. There are many DOP maps, such as this Galileo HDOP map by the Galileo System Simulation facility, but after a quick search in the literature I couldn’t find any survey paper that made a comprehensive comparison. The closest thing I found to what I was looking for was Consellation design optimization with a DOP based criterion, by Dufour etl. This was published in 1995, so it compares the GPS and GLONASS constellations with prototypical constellations such as the Walker delta using different parameters, but it doesn’t mention Galileo, which wasn’t even planned back then.
Therefore, I have decided to do my own simulations and compare the DOP for the Galileo and GPS constellations. Since the actual distribution of the satellites can differ substantially from the slots designated in the constellation, I am considering both the theoretical reference constellations and the real world constellations, as taken from the almanacs at the beginning of 2020. This post is a detailed account of my methodology and results.
Simulation methodology
The structure of the simulations is as follows. Given a certain satellite constellation, first we compute the positions of all the satellites in the constellation for a certain time interval. The positions are computed in an ECEF reference frame, and the length of the time interval is the repetition period of the constellation, which is one sidereal day in the case of GPS and 10 sidereal days in the case of Galileo. A grid of time steps separated roughly one minute is used.
Then, for a grid of observers on the Earth surface, spaced one degree in longitude and one degree in latitude, the different DOP metrics (GDOP, PDOP, HDOP and VDOP) are computed at each time step, taking into account only the satellites above a 5 degree elevation mask. The resulting DOPs can then be averaged across time, or the maximum value can be taken, depending on whether we are interested in studying the mean DOP or the worst DOP.
The reason for choosing the repetition period of the constellation as the simulation time interval is that since this period is an integer number of sidereal days for the constellations under consideration, the relative positions of the observers and satellites (and hence the DOPs) are periodic functions, with the same period as the constellation. However, this is only true if we ignore the precession of orbital planes due to the oblateness of Earth and other perturbations.
The rate of orbital plane precession (rate of right ascension of the ascending node) for the GNSS MEO constellations, is slow: -15.28 degrees/year for GPS and -10.09 degrees/year for Galileo. The geometry of the constellation, and hence the geographical distribution of the DOPs with respect to longitude will drift at these rates. These means that if we are interested in relatively short time spans of days or a few months, the distribution of the DOP can depend on the longitude. However, if we are interested in longer time spans of several years, the average or worst DOP no longer depends on the longitude.
Therefore, we simulate the constellation during a repetition period starting at 2020-01-01 00:00:00 UTC to show the geographical dependence on DOP for short time spans near the beginning of 2020. For other short timestamps, the resulting distribution should be shifted to the west for 15.28 degrees/year for GPS and 10.09 degrees/year for Galileo. To show the long-term behaviour, we eliminate the dependency of DOP on longitude by taking the average or the maximum across all longitudes for each fixed latitude.
Orbit model
The modelling of the satellite orbits follows the Keplerian model plus a perturbation consisting of a constant rate of right ascension of the ascending node \(\dot{\Omega}\). The model allows the specification of the mean motion \(n = \dot{M}\) to account for a constant perturbation in the mean motion. Otherwise, the mean motion is computed with the usual formula \(n = \sqrt{\mu/a^3}\). This is used for the Galileo constellation, which specifies n = 613.72253566 degrees/day, even though the formula yields 613.72254178 degrees/day. However, the difference between these two values is an insignificant 0.002 degrees/year.
Circular orbits are used for all the satellites, though the model supports non-circular orbits and a constant rate of argument of periapsis \(\dot{\omega}\) parameters.
To transform between ECI and ECEF coordinates, the rotation of the Earth is modelled in a simple way. We consider that the Z axis of the ECI and ECEF coordinates coincide and that the angle between the X axis in the ECI frame (vernal equinox) and ECEF frame (Greenwhich meridian) is given by the Earth rotation angle, computed from the formula given here with UTC instead of UT1. These are approximations introduced because the accurate conversion of GCRS to ICRF coordinates using Astropy is much more expensive.
The semimajor axis \(a\), inclination \(i\) and rate of right ascension of the ascending node \(\dot{\Omega}\) of all the satellites are set equal to the nominal constellation value. This simplified model is deemed sufficient for the DOP simulations presented here.
Galileo constellation
The Galileo nominal constellation is a Walker 24/3/1 constellation, consisting of 24 satellites in 3 orbital planes. The reference constellation parameters are described here (note that there is a typo in that listing and slots B2 and B7 are swapped).
The constellation is designed to have 6 additional spare satellites, but the positions of the spares haven’t been published anywhere (or at least I haven’t been able to find it). Teunissen etl. in their Springer Handbook of Global Navigation Satellite Systems make an educated guess about the positions of the spares, with two diametrically opposed spares per orbital plane, and a between-plane phasing opposite to that of the Walker constellation.
The status of the constellation at the beginning of 2020 is as follows. A total of 26 satellites have been launched. Two of these are the eccentric satellites E14 and E18, and are not considered in this study. The other 24 are occupying all the slots of the Walker constellation. However, two of them, E20 and E22, are not operational. No satellites are occupying spare slots.
To compare the constellation defined by the almanac for the first week of 2020 with the reference constellation, it is necessary to bring the two constellations to a common epoch. I have moved the almanac to 2016-01-01 00:00:00 UTC, the epoch of the reference constellation, by applying the nominal \(\dot{\Omega}\) and \(\dot{M}\) rates. The comparison of the constellations can be seen in the figure below.

We see that there is a small difference in the RAAN of the almanac and reference constellations and a noticeable difference in mean anomaly of almost half of the in-plane phasing angle. These may be caused by perturbations not covered by the nominal drift rates. Nevertheless, the real constellation is well phased. The non-operational satellites E20 and E22, which occupy slots C5 and B3 are not included in the almanac.
GPS constellation
The reference constellation for GPS contains 24 satellites in 6 orbital planes. However, an expandable constellation is also defined where four particular slots (each in a different plane) can be split in two in order to accommodate up to 27 satellites. The details of the 24-satellite baseline constellation and the expandable slots are defined here.
The status of the GPS constellation at the beginning of 2020 is as follows. There are 31 operational satellites, all of them included in the almanac. The satellite G04, which is GPS-III SV01 entered service on 2020-01-13, so it is considered as operational for this study even though it was marked as unhealthy in the almanac for the first week of 2020.
As GPS is a much older constellation than Galileo, the configuration of the operational satellites differs much more from the reference constellation, as shown in the figure below, which is referenced to the GPS constellation reference epoch of 1993-07-01 00:00:00 UTC.

The figure shows a similar configuration to this image, which shows the status of the constellation on 2019-07-01. Besides the difference in RAAN and mean anomaly between the almanac and reference constellations owing to the long propagation interval between 2020 and 1993, there are the following important differences.
There are satellites which occupy slots that don’t exist in the reference constellation. These are: G19, which occupies slot C5; G22, which occupies slot E6; G13, which occupies slot F6; and G04, which is listed in slot A6, but is actually very close to G25 in slot F4.
Additionally, G11, which occupies slot D5 (the expanded slot D2F) is actually halfway between plane C and plane D; and G14, which occupies slot F5 (the expanded slot F2F) is between F1 and F4 instead of being between F2 and F3 (i.e., in G13’s position at F6).
The planes of the constellation are not so well kept as for Galileo, owing to the older age of the constellation and probably to the higher station-keeping costs given by resonances with the Earth’s zonal harmonics, due to the orbital period of half a sidereal day.
In summary, the real GPS constellation nowadays only resembles the reference constellation vaguely. Thus, the reference constellation is something that only exists on paper and studies of the performance of the constellation, such as this post, should use the real constellation taken from the almanac.
Results
The average DOPs depending on latitude and longitude are shown in the figures below (you can click them to view them in full size).

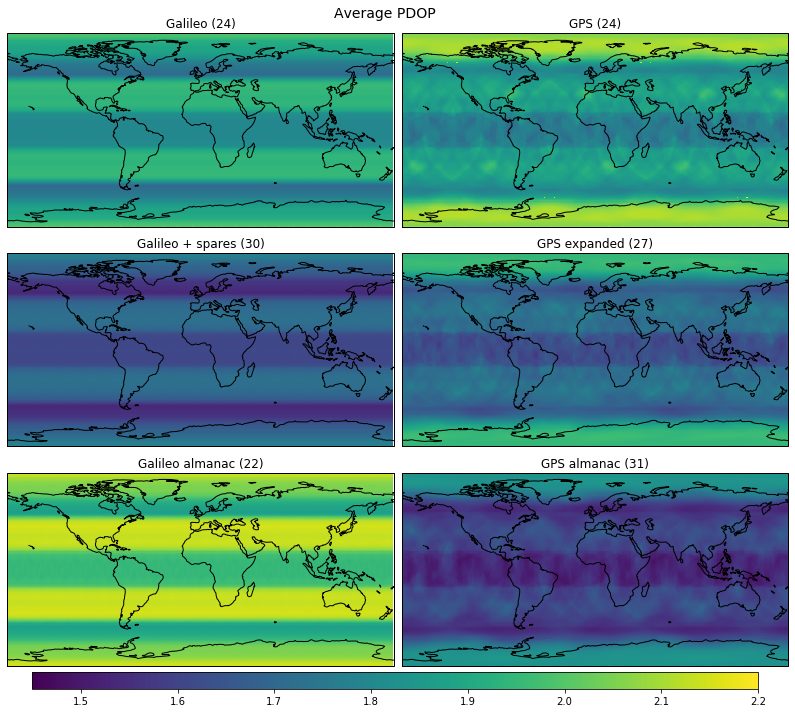
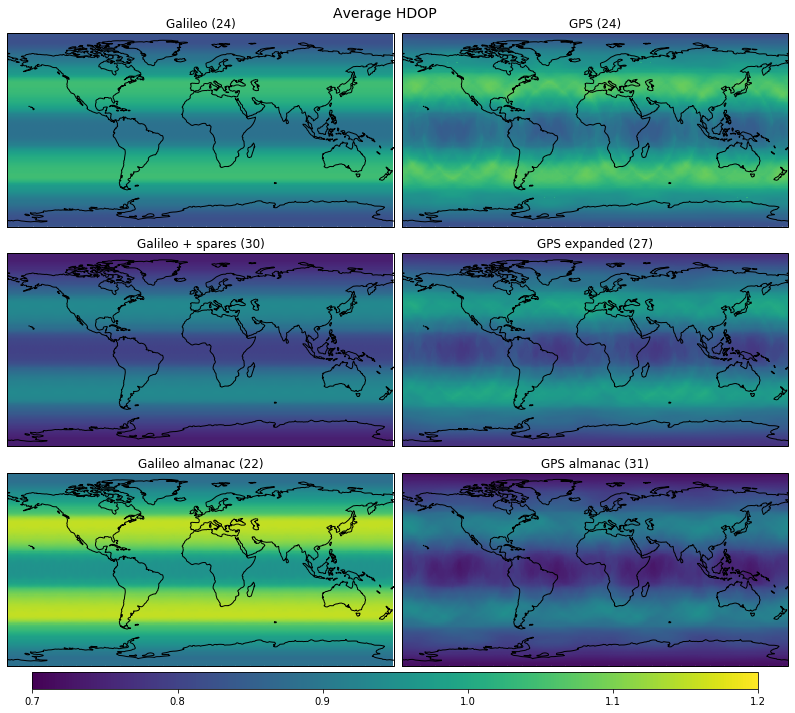
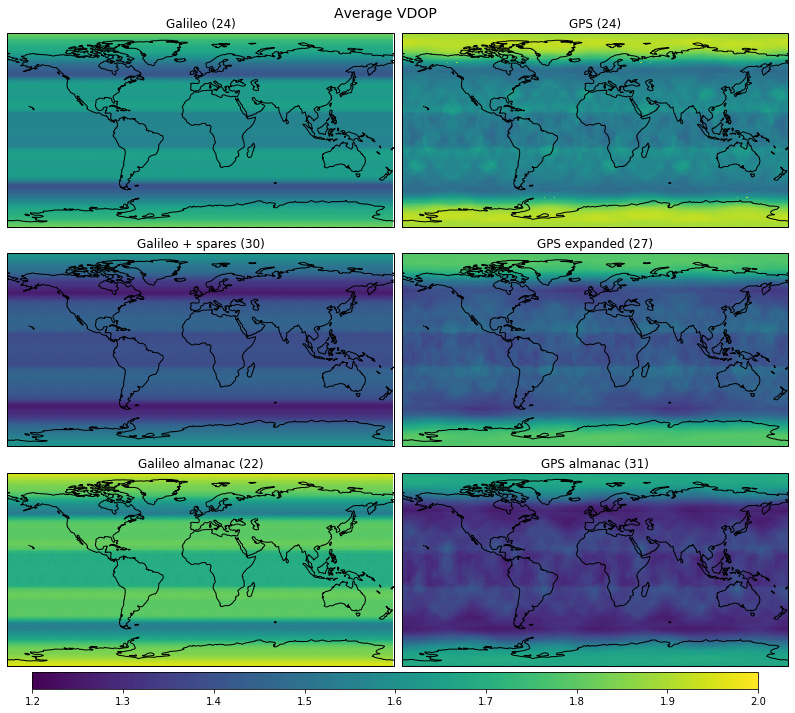
The real Galileo constellation, as taken from the almanac, has the worst performance, since it only has 22 satellites.
In the GPS constellations we observe a certain dependence of the DOP on the longitude, while in the Galileo constellations it is almost inexistent. The main reason for this is that the GPS ground tracks repeat after 2 orbits (one sidereal day), so the relation of the longitude of the observer with respect to the RAANs of the orbital planes makes a noticeable effect. For Galileo, the ground tracks repeat after 17 orbits (10 sidereal days), so the observer sees the planes from different orientations until the ground tracks repeat, and the longitude dependent effects average out.
The figures below show the worst DOPs depending on latitude and longitude.

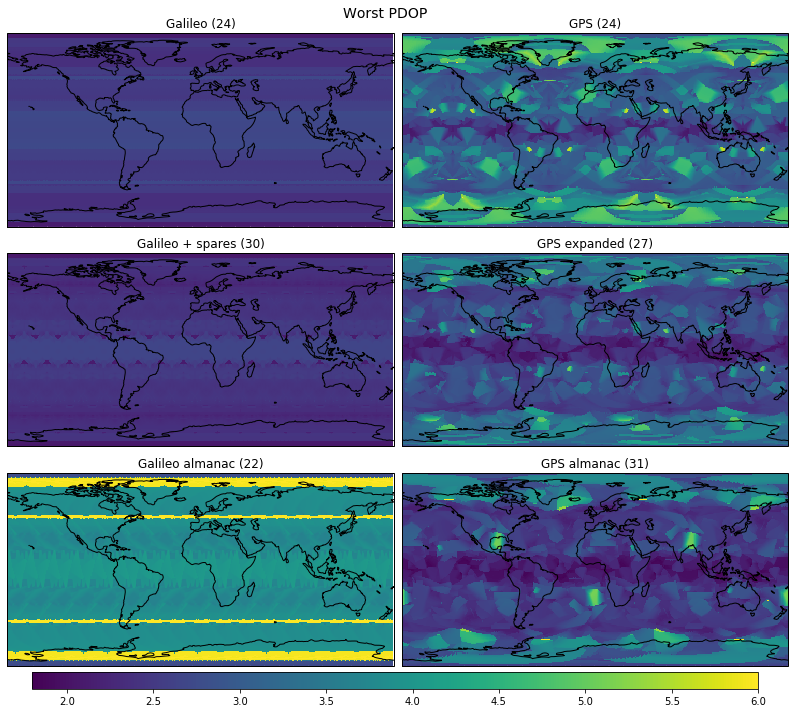
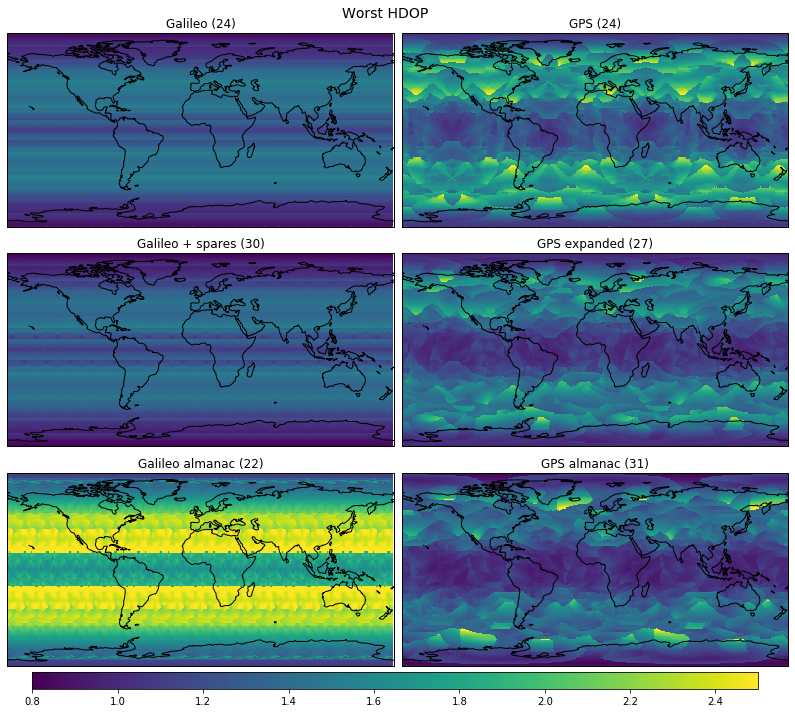
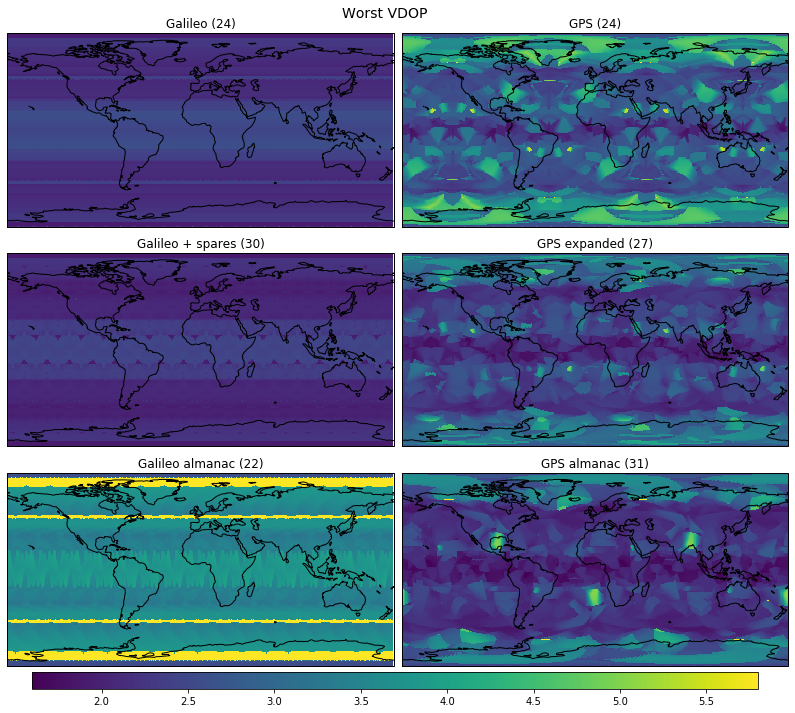
The dependency on longitude of GPS causes bad spots, where the DOP is much larger. Even the real 31 satellite constellation taken from the almanac has a few of these spots.
On the other hand, the Walker type constellation of Galileo averages things out completely and provides a more uniform and generally better performance. Note however that some dependence on the longitude comes back once the symmetry of the Walker constellation is broken by introducing 6 spare satellites or by removing the two inactive satellites to obtain the current almanac constellation.
Incidentally, the current Galileo constellation shows very bad worst VDOP for latitudes near 50 degrees.
Now we eliminate the dependence on longitude by taking the average across longitude for the case of average DOP and the maximum for the case of worst DOP. The figures below show the average DOPs.
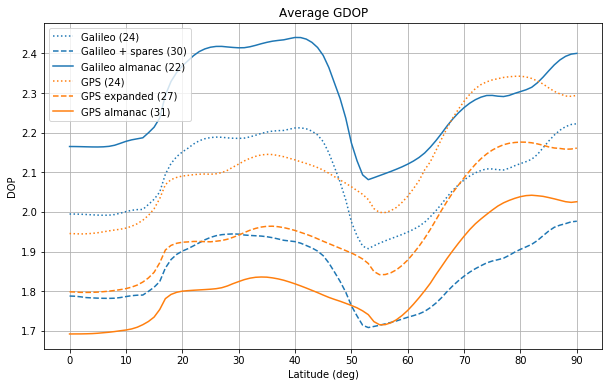
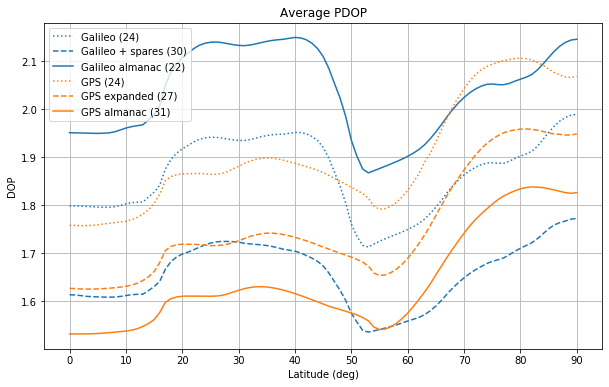
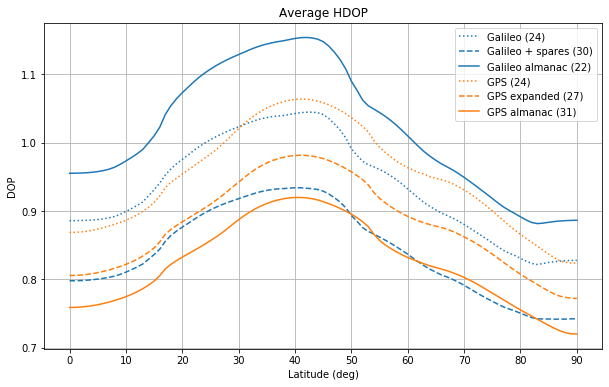
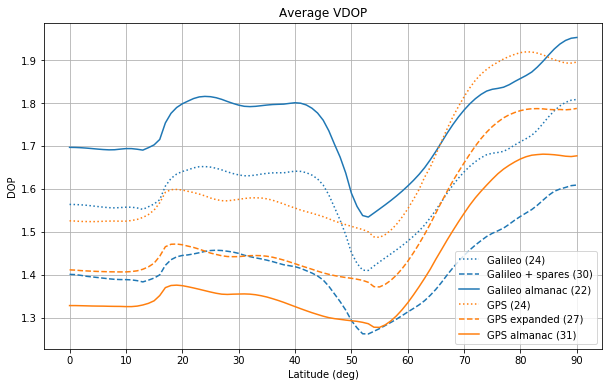
These plots show that all the constellations have the same qualitative behaviour. The HDOP grows from the equator until around 45 degrees and then decreases towards the poles, where it attains its minimum value. The VDOP plateaus between approximately 20 and 45 degrees, then attains its minimum around 55 degrees and grows towards the poles, where it attains its maximum. The GDOP and PDOP are dominated by the behaviour of the VDOP.
The figures below show the worst DOPs.
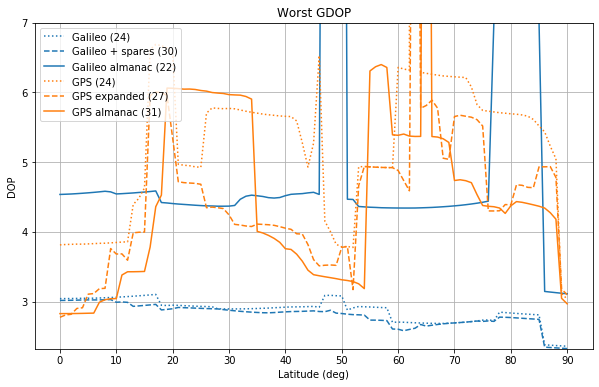
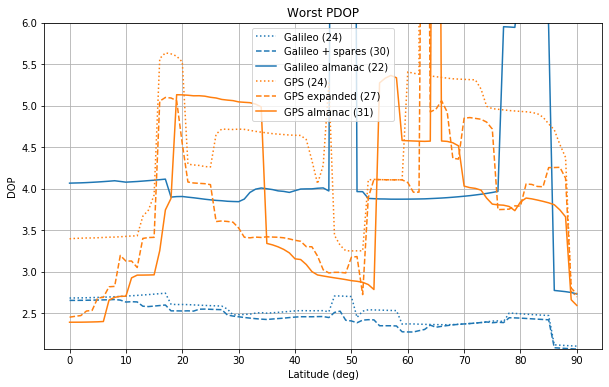
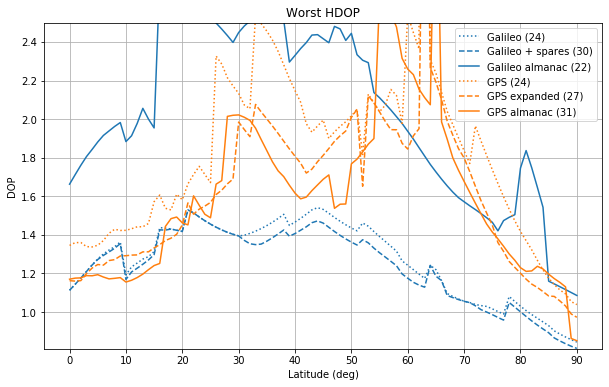
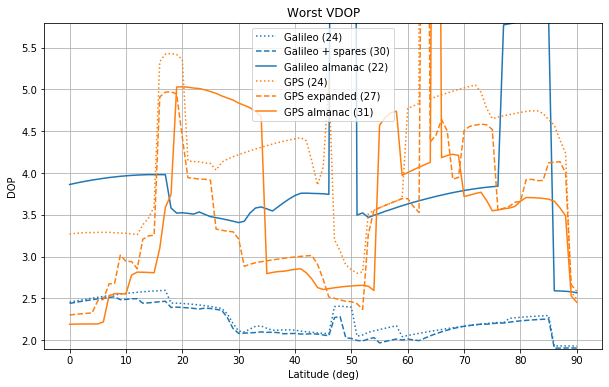
We see that the current Galileo constellation has very large VDOPs for latitudes between 45 and 50 degrees and for latitudes around 80 degrees. All the GPS constellations have very large DOPs around 62 degrees. Interestingly, the addition of the 6 spares satellites to the Galileo Walker 24/3/1 constellation makes little improvement to the worst DOP.
We see that the Galileo Walker configuration gives a much flatter, and generally much better worst DOP performance than the GPS constellation. As remarked by Dufour etl., the GPS constellation was not designed with worst DOP performance in mind, but rather with tolerance to satellite failures.
Code and data
The code used in this post can be found in this Jupyter notebook. The almanac data, as well as the files storing the DOP results can be found in the same Gihtub repository.
One comment