In my previous post I decoded LTE PDSCH (physical downlink shared channel) transmissions from an IQ recording that I had made of an eNB recording using an USRP B205mini and a single antenna. The eNB has two antenna ports, and it uses TM4 (closed-loop spatial multiplexing) to transmit the PDSCH to each individual UE. In the post, I repeated several times that two-codeword TM4 is intended for 2×2 MIMO and relies on the receiver having at least 2 antennas in order to separate the two transmitted codewords, so I couldn’t decode these transmissions with my recording.
In this post I will show that in some cases this is not true, and these two-codeword TM4 transmissions can be decoded with just one receive antenna. I will decode some of these two-codeword transmissions from my IQ recording by using the ideas I introduce below.
Single-codeword equalization
The main idea I exploit here is that some of these two-codeword TM4 transmissions are low coding rate QPSK transmissions. For such a transmission, each of the bits from the Turbo encoder output is repeated several times in the PDSCH transmission. Each of these repetitions is scrambled with a different bit from the scrambling sequence. We can try to decode one of the two codewords as if it was a single-codeword TM4 transmission, and treat the other codeword as interference. Since the two codewords use different scrambling sequences, when the soft symbols for each Turbo encoder output bit are collected and averaged (or summed), the other codeword will tend to cancel out due to the mismatch of the scrambling sequences.
In effect, a low coding rate two-codeword transmission behaves somewhat as a CDMA system. The two codewords can be separated not only because they have different spatial characteristics (which we cannot exploit with a single antenna), but also because they are “coded” with different scrambling sequences. To apply this idea, it is critical that the codewords are modulated with QPSK (or at least the codeword we attempt to decode). The idea doesn’t work with higher-order constellations because demodulating a higher-order constellation to obtain LLRs is inherently a non-linear process, unlike with QPSK. For instance, if we have a two-codeword transmission with the two codewords modulated in 16QAM and obtain the LLRs for one of the codewords, these LLRs will be completely wrong due to the other codeword acting as interference. It is quite difficult that averaging from the repetition coding will fix this. However, for QPSK the LLRs depend linearly on the other codeword, so averaging reduces the power of the other codeword by one over the number of averages.
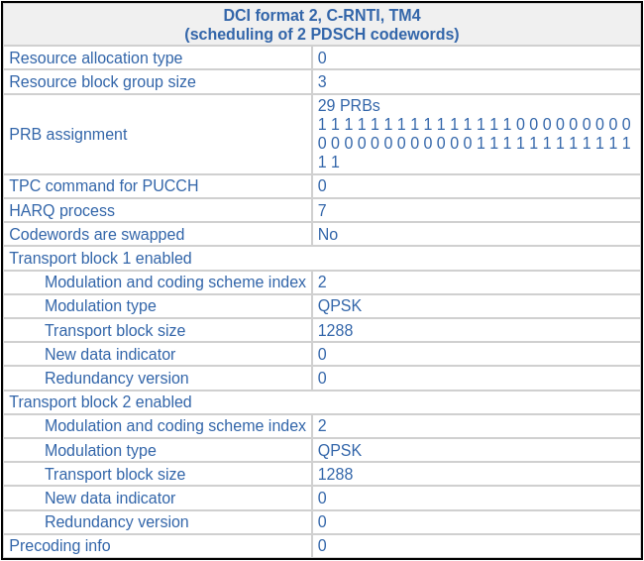
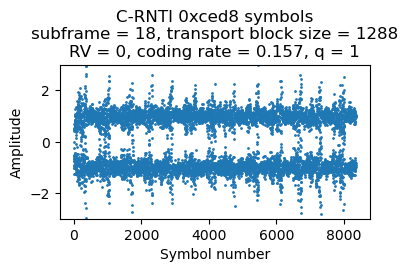
To show this in action, let’s decode this two-codeword transmission from C-RNTI 0xced8, which appears in subframe 18. The coding rate is 0.16, which is quite low.
A look at the precoding matrices in my post about TM4 shows that precoding info 0 is equivalent to simultaneously transmitting the first codeword as single-codeword with precoding info 1, and the second codeword as single-codeword with precoding info 2, except that the two codewords are also divided by an additional \(\sqrt{2}\) factor so that the average total transmitted power stays the same.
Therefore, to decode the first codeword, we can pretend that this is a single-codeword TM4 transmission using precoding info 1, except that we need to multiply the symbols by \(\sqrt{2}\) after equalization. If we do this, the symbols look quite bad, due to the second codeword acting as interference.
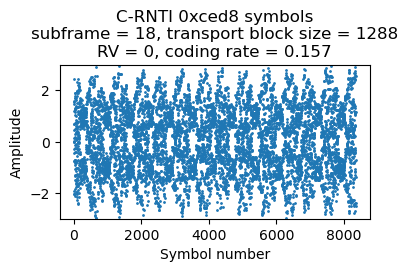
Nevertheless, after soft-combining of the repetitions of each Turbo codeword bit, this is how the LLRs look like. They are still quite noisy, but we are starting to see that the values accumulate at positions away from the centre.
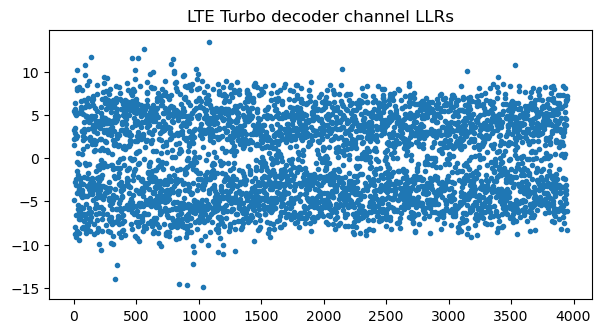
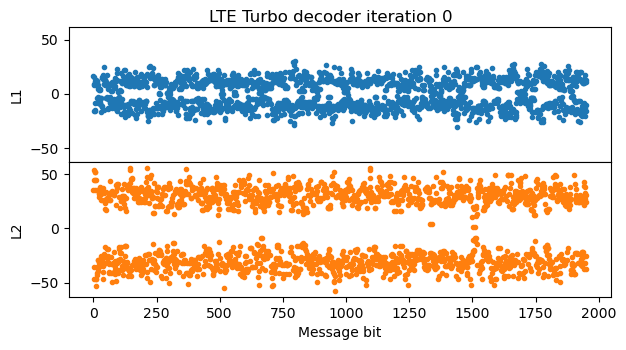
The first iteration of the BCJR decoder is enough to correct all the bit errors. The following iterations increase the LLRs even more. So this codeword can be decoded without issues.
Now we try the same approach with the second codeword, using precoding info 2 instead of 1. We also need to set \(q = 1\) (the codeword number) in the generation of the scrambling sequence. The equalized symbols look even worse than for the first codeword.
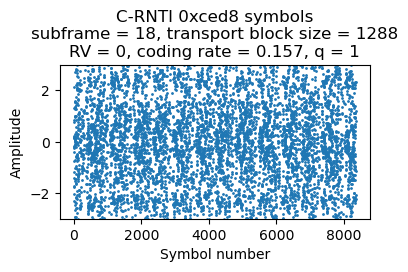
Even if we perform soft-combining for the repetitions of the Turbo codeword bits, there is no trace of the codeword. The LLRs look almost like Gaussian noise.
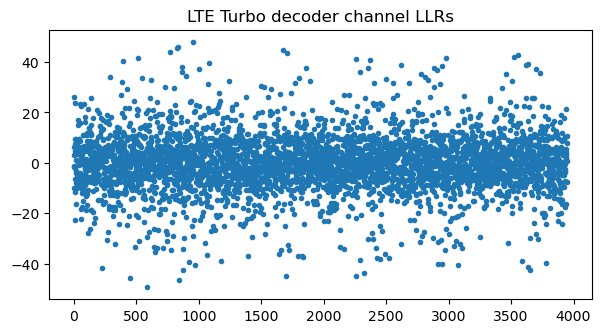
After 10 iterations the Turbo decoder has perhaps managed to correct some short sections of the message, but most of the message is still full of bit errors. Therefore, this approach doesn’t work to decode the second codeword.
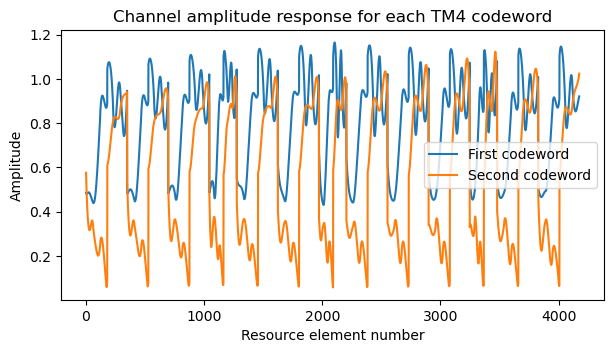
The problem here is that the second codeword is much weaker than the first one. The channel amplitude for each codeword is determined by \(|h_0 + h_1|\) and \(|h_0 – h_1|\) respectively, where \(h_j\) denotes the channel response from transmit antenna port \(j\) to the receive antenna. This is because the precoding vectors for the first and second codeword are essentially \((1, 1)^T\) and \((1, -1)^T\) in this case.
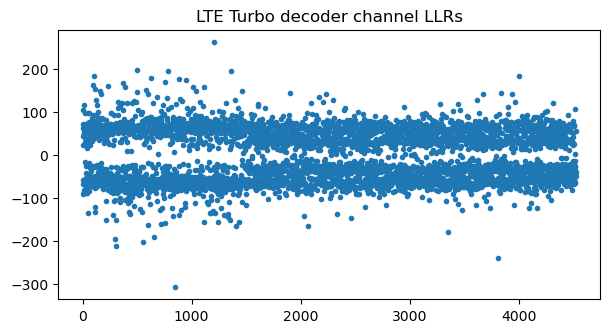
Since we have an estimate for \(h_j\) from the measurement of the CRS (cell-specific reference signals), we can plot the channel amplitude for each codeword. The plot is more or less periodic because the resource elements are ordered by time and frequency, and the channel depends mostly on the frequency. We can see 13 periods because there are 13 symbols occupied by the PDSCH (the CFI is 1). The periods corresponding to some symbols are shorter due to the presence of CRS in that symbol. We can see that in many parts of the spectrum the first codeword is much stronger than the second one. This means that the SNIR (signal to noise plus interference ratio) of the second codeword is much worse, and the soft-combining that is possible due to the low coding rate is not sufficient to improve the SNIR enough.
In general, this method will work or not depending on the relative channel amplitudes of the two codewords and on the amount of repetition coding present. However, now that we have managed to decode the first codeword, there is a method to decode the second codeword. The method is sometimes called successive interference cancellation.
Successive interference cancellation
This methods works as follows. When there are several overlapping transmissions (of any kind; they don’t need to be LTE waveforms), first the strongest transmission is decoded, treating the rest as interference. If it can be decoded successfully, the data is remodulated and subtracted from the received signal (this requires an estimate of the channel for this transmission). This removes the contribution of the strongest transmission except for some small amount of power due to the error in the channel estimate. Then the second strongest transmission can be decoded. In this way, the overlapping transmissions can be decoded and cancelled out in order of decreasing power.
In our case, we have successfully decoded the transport block from the first codeword. We encode this by applying the Turbo encoder and rate matching, and modulate it using the channel estimate obtained from the CRS measurements. The cancellation is done at the level of resource elements, before equalization (we do not apply an IFFT to pass to the time domain). Once the contribution from the first codeword is cancelled, we try to decode the second codeword in the same way as before, obtaining the following symbols (before soft-combining). Clearly this has enough SNR to be decoded, and indeed this is the case. Just with soft-combining we reduce the number of bit errors to a few, which the Turbo decoder can fix in the first BCJR run.
Other transmissions for C-RNTI 0xced8
There is another transmission for C-RNTI 0xced8 in which we can use this approach. It appears in subframe 221. This is its DCI.
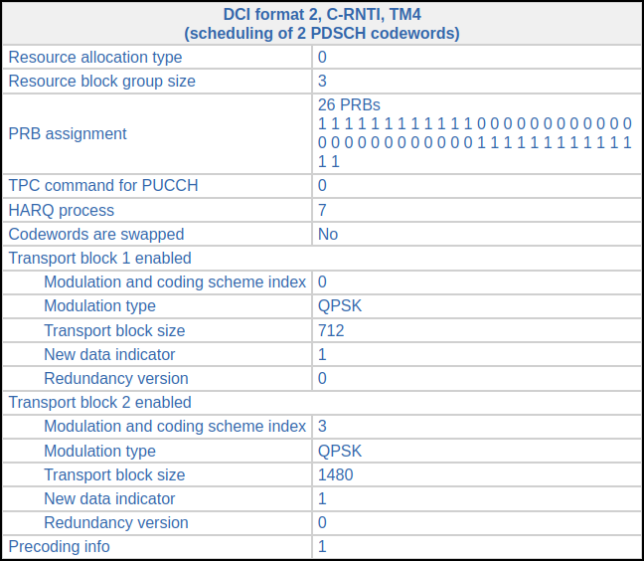
Now the precoding info for the two-codeword transmission is 1, so the precoding matrices that we need to use for single-codeword decoding are those with indices 3 and 4. The first codeword is shorter. It has a rather low coding rate of 0.1. Its symbols are shown below.
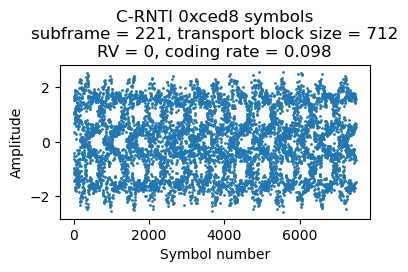
Soft combining works quite well, giving only a few bit errors. In this plot we can also see how the first symbols of the Turbo codeword (until symbol 800 approximately) are repeated one time more than the others, so they gain slightly more LLR from soft combining. The Turbo decoder can correct all the bit errors and decode the transport block successfully.
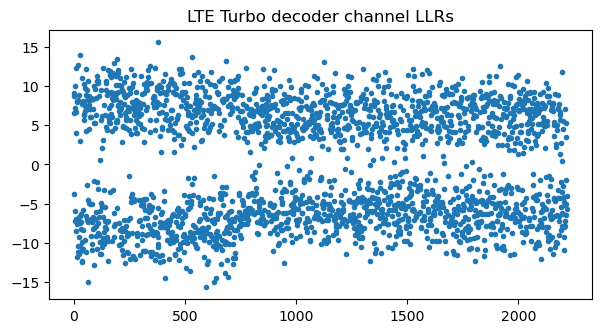
As in the case of the previous transmission, the equalization of the second codeword looks really bad. This codeword has a higher rate of 0.2, which doesn’t help.
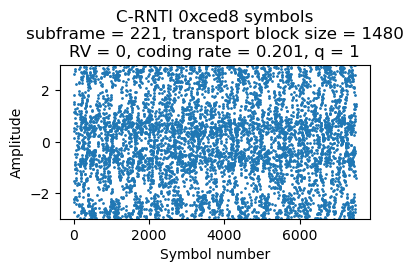
The soft combining of the symbols looks almost like random noise, and the Turbo decoder is not able to decode this codeword successfully.
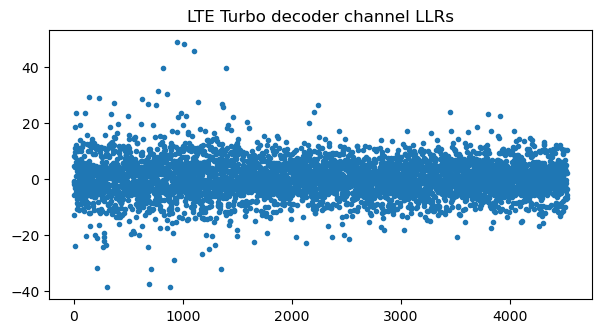
Looking at the channel amplitudes for each of the codewords we see why the decoding of the second codeword has failed: it has much less power than the first codeword in most of the spectrum. Observe that these channel amplitudes are different from the ones for the previous transmission, since now the amplitudes are \(|h_0 + i h_1|\) and \(|h_0 – i h_1|\) due to the use of precoding matrix 1 (instead of 0) in the two-codeword TM4 transmission.
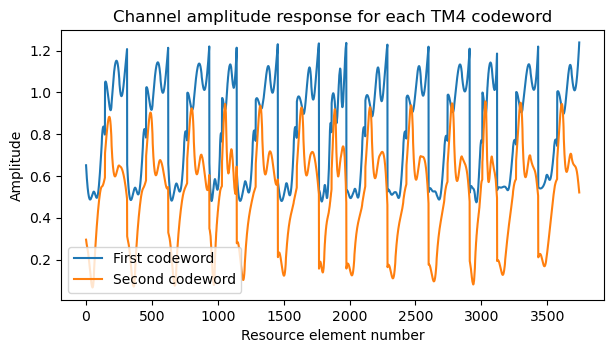
Since we have decoded the first codeword successfully, we can perform successive interference cancellation. The symbols for the second codeword after cancellation of the first one look good, except in the regions of the spectrum where the channel amplitude almost has a null. Soft combining and Turbo decoding will correct the errors in these regions.
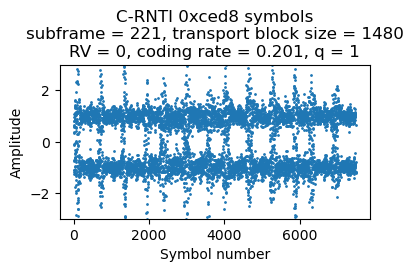
The output of the soft combining looks reasonably good. There are some bit errors that the first BCJR of the Turbo decoder can correct.
There are no other transmissions for C-RNTI 0xced8. The only four transmissions that appear in the first 500 ms of the recording are these two two-codeword TM4 transmissions, and a retransmission of the first codeword of each of these two transmissions. The retransmissions are done with single-codeword TM4, and I already decoded them in the previous post.
QAM transmissions
As we saw in the previous post, all the transmissions for C-RNTI 0xcee3 use two-codeword TM4 with 16QAM or 64QAM, except for the first four transmissions, which are single-codeword QPSK, and a retransmission of a single codeword using 64QAM. I decoded all these single-codeword transmissions in that post. For the two-codeword QAM transmissions we cannot apply the technique described in this post. As discussed, QAM demodulation is a non-linear process, so soft-combining doesn’t help much to reduce the interference from the other codeword. Moreover, these transmissions use a coding rate higher that 1/3, because the UE is reporting a high CQI. This means that there are no repeated symbols from the Turbo codeword that can be soft combined.
Nevertheless, we can cheat and decode one of these two-codeword transmissions. The trick is that we have managed to decode the first transport block of the transmission when it was retransmitted as a 64QAM single-codeword TM4 transmission. We can perform successive interference cancellation to decode the second transport block, which is modulated with 64QAM. Then we can perform successive interference cancellation of this second codeword in order to decode the first codeword. Although we already have decoded the first codeword when it was retransmitted, this is interesting because in the initial transmission it was modulated with 16QAM instead of 64QAM.
The transmission that we are going to decode was done in subframe 327 and it has the following DCI.
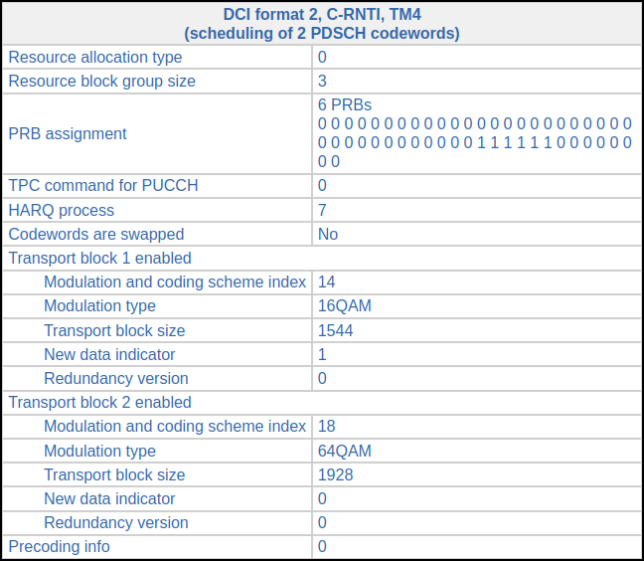
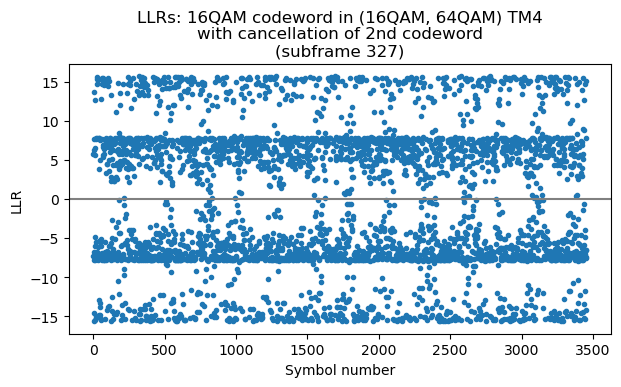
The first transport block was retransmitted as single-codeword 64QAM in subframe 335. As we have decoded this transmission, we can remodulate the first codeword (using 16QAM) and cancel it in the two-codeword transmission. Then we equalize for the second codeword, obtaining the following constellation, which barely resembles 64QAM.
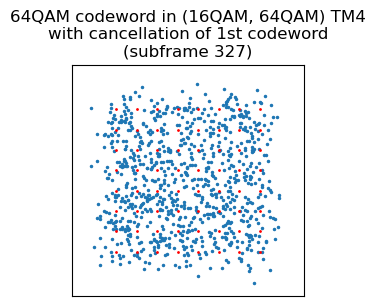
Nevertheless, the LLRs are much better than what appears from the constellation plot. Higher order QAM constellations are not so much about discerning individual constellation points, but rather about locating symbols around a certain part of the constellation diagram, because nearby constellation points usually differ by one or two bits. These are the LLRs obtained with a noise sigma of 0.2. Only a relatively small portion of the bits have LLRs close to zero.
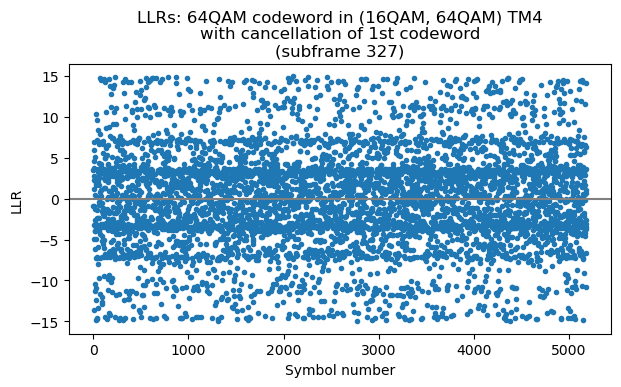
In the first iteration the Turbo decoder is able to fix most of the bit errors.
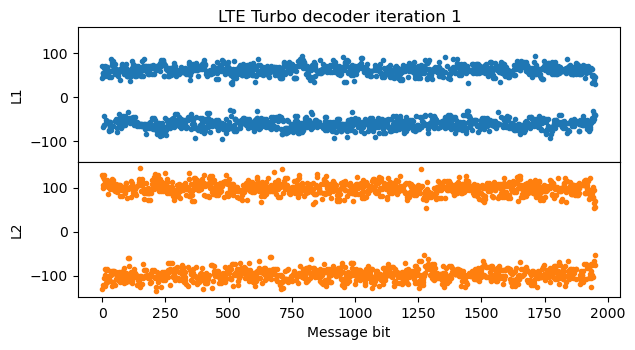
The second iteration fixes the remaining bit errors, so the codeword is decoded successfully.
Now that we have the second transport block, we can remodulate it and cancel it from the two-codeword transmission. Equalizing for the first codeword, we obtain a 16QAM constellation. It is reasonable clean, with not many symbol errors.

The LLRs look quite good. There are only a few bit errors, corresponding to areas of the spectrum where the channel amplitude for this codeword is weaker. The first run of the BCJR decoder is able to correct all the bit errors.
Wireshark analysis of new MAC PDUs
Let us now analyse in Wireshark the MAC PDUs that we have been able to decode using these techniques. They give some additional data for the question I had in the previous post about whether I was interpreting LCID 3 correctly as containing RLC AM PDUs.
After decoding the two transmissions for C-RNTI 0xced8 shown above, we now have the following 5 MAC PDUs for this C-RNTI. Packets number 4, 5, and 54, 55 are the ones from the new two-codeword TM4 transmissions. Packets 9 and 60 were already decoded in the previous post and are retransmissions of packets 4 and 54, so they contain exactly the same data.
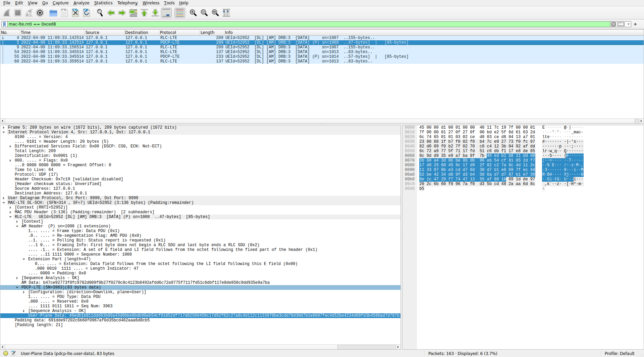
0xced8Something interesting happens in packets 5 and 55. They contain the end of an RLC SDU followed by a complete 85-byte RLC SDU. Wireshark dissects this second SDU as PDCP. The data in the PDCP header looks reasonable, and the sequence numbers of these PDCP PDUs are 3963 and 3966 respectively. Seeing this I’m quite sure that LCID 3 uses the RLC AM protocol, because it would be too much of a coincidence to get all this consistent data by chance.
The logical explanation for why the sequence numbers are not consecutive, even though now we are decoding all the PDSCH transmissions for C-RNTI 0xced8 is that this UE must be simultaneously getting data from another cell, which doesn’t appear in the recording. Assuming two-codeword TM4 transmissions, two transmissions that we don’t see would carry AM PDUs with sequence numbers 1009 and 1010, and 1011 and 1012. The PDCP PDU that ends in the AM PDU with sequence number 1014 must have sequence number 3965, and must begin in one of the missing AM PDUs (since it has already started by AM sequence number 1013). In the AM PDU 1009, the other PDCP PDU, with sequence number 3964 should begin.
For C-RNTI 0xcee3, the only new MAC PDU is packet 86, which is the second codeword of the 16QAM/64QAM transmission that we have decoded. This contains an AM PDU with sequence number 64, which has continuation data of the same RLC SDU as the first codeword in that transmission (packet 85, AM sequence number 63).
0xcee3Code and data
I have updated the Jupyter notebook and the PCAP file with the work done in this post.