Yesterday I posted about how to compute the well known formula for the bit error rate of FSK with non-coherent demodulation. Later I realized that the same kind of argument can be extended to cover the case of \(m\)-FSK in which the \(m\) tones are orthogonal. The formula for this is not so well known, and I don’t recall having seen it before, although surely it is somewhere in the literature. Here I show the calculations and the closed-form expression that is obtained.
Recall from the previous post and the post about m-FSK symbol error rate that the symbol error rate for \(m\)-FSK is\[\mathrm{SER} = 1 – \int_{-\infty}^{+\infty} G(t)^{m-1} g_\lambda(t)\,dt,\]where \(G(t)\) is the cumulative distribution function of the chi-squared distribution with two degrees of freedom, \(g_\lambda(t)\) is the probability density function of the non-central chi-squared distribution with two degrees of freedom and non-centrality parameter \(\lambda = 2E_s/N_0\). Since \(g_\lambda(t)\) is a probability density function and \(g_\lambda(t) = 0\) for \(t < 0\), this expression can be rewritten as\[\mathrm{SER} = \int_{-\infty}^{+\infty} (1 – G(t)^{m-1}) g_\lambda(t)\,dt = \int_0^{+\infty} (1 – G(t)^{m-1}) g_\lambda(t)\,dt.\]
The cumulative distribution function of the chi-squared distribution with two degrees of freedom is \(G(t) = 1 – e^{-t/2}\) for \(t \geq 0\). Therefore,\[1 – G(t)^{m-1} = 1 – \sum_{k=0}^{m-1} {m – 1 \choose k} (-1)^k e^{-kt/2} = \sum_{k=1}^{m-1} {m – 1 \choose k} (-1)^{k+1} e^{-kt/2}.\]Replacing this in the expression for the symbol error rate we get\[\mathrm{SER} = \sum_{k=1}^{m-1} {m – 1 \choose k} (-1)^{k+1} \int_0^{+\infty} e^{-kt/2} g_\lambda(t)\,dt.\]Since\[g_\lambda(t) = \frac{1}{2}e^{-(t+\lambda)/2}I_0(\sqrt{\lambda t}),\]where \(I_0\) is the modified Bessel function of the first kind, we have\[\mathrm{SER} = \frac{e^{-\lambda/2}}{2} \sum_{k=1}^{m-1} {m – 1 \choose k} (-1)^{k+1} \int_0^{+\infty} e^{-(k+1)t/2} I_0(\sqrt{\lambda t})\, dt.\]
Now we use the relation\[\int_0^{+\infty} e^{-ax}I_0(b\sqrt{x})\,dx=\frac{1}{a}e^{b^2/(4a)},\]which I indicated how to prove in the previous post (expand the Bessel function in power series and compute the integrals that appear using integration by parts and induction). This gives\[\begin{split}\mathrm{SER} &= \frac{e^{-\lambda/2}}{2} \sum_{k=1}^{m-1} {m – 1 \choose k} (-1)^{k+1} \frac{2}{k + 1} e^{\lambda/(2(k+1))}\\ &= \sum_{k=1}^{m-1} {m – 1 \choose k} \frac{(-1)^{k+1}}{k + 1} e^{-\lambda k/(2(k+1))} \\ &= \sum_{k=1}^{m-1} {m – 1 \choose k} \frac{(-1)^{k+1}}{k + 1} e^{-\frac{E_s}{N_0}\cdot\frac{k}{k+1}}.\end{split}\]This expression cannot be simplified further, but it provides a better way to compute the symbol error rate than solving the integral numerically, which is what I did in the earlier post about m-FSK.
To compute the bit error rate in terms of the \(E_b/N_0\), recall from that post the relation\[\mathrm{BER} = \frac{m}{2(m-1)} \mathrm{SER},\]and also that\[\frac{E_b}{N_0} = \frac{1}{\log_2(m)} \frac{E_s}{N_0}.\]
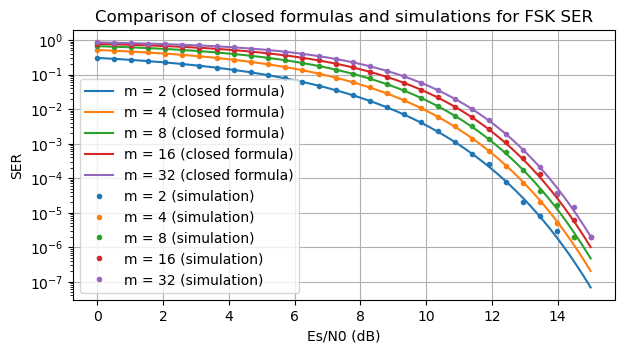
To validate this formula, I have extended the Jupyter notebook that I used in the m-FSK SER post to compare this formulas with simulation results. The following plot shows a good match between the SER closed-form formula and the simulations.
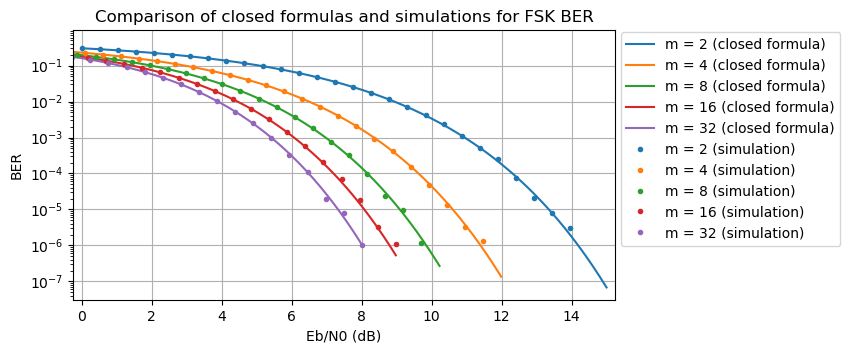
Rescaling the plot in terms of BER versus Eb/N0 shows the sensitivity gain achieved by increasing the number of tones, which is a well known fact.